Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

ОБ ОДНОМ ЧАСТНОМ РЕШЕНИИ ПРОСТРАНСТВЕННОЙ ЗАДАЧИ ГИПЕРЗВУКОВОГО ОБТЕКАНИЯ ТОНКОГО КРЫЛА ПЕРЕМЕННОЙ ФОРМЫ

Научная статья
Богатко В. И.
Потехина Е. А.
DOI:
https://doi.org/10.23670/IRJ.2017.55.017
Выпуск: № 1 (55), 2017
Опубликована:
2017/01/25
PDF

Богатко В.И.1, Потехина Е.А.2

1ORCID: 0000-0002-6247-6405, кандидат физико-математических наук, доцент, 2ORCID: 0000-0002-4307-3205, кандидат физико-математических наук, старший научный сотрудник, Санкт-Петербургский государственный университет

ОБ ОДНОМ ЧАСТНОМ РЕШЕНИИ ПРОСТРАНСТВЕННОЙ ЗАДАЧИ ГИПЕРЗВУКОВОГО ОБТЕКАНИЯ ТОНКОГО КРЫЛА ПЕРЕМЕННОЙ ФОРМЫ

Аннотация

Работа посвящена дальнейшему исследованию задачи обтекания тонкого крыла переменной формы гиперзвуковым потоком газа. Головная ударная волна считается присоединенной к передней кромке крыла, по крайней мере, в одной точке.  Решение строится с помощью метода тонкого ударного слоя. При определении поправок первого приближения два уравнения полученной системы могут быть проинтегрированы независимо от остальных. Введение новой функция и применение преобразования Эйлера-Ампера позволяет построить решение, зависящее от двух произвольных функций и неизвестной формы фронта головной ударной волны. Для определения этих функций получена интегро-дифференциальная система уравнений. В настоящей работе приведен один из вариантов полуобратного метода построения решения, при котором задается вид одной из произвольных функций. Форма обтекаемого тела находится в процессе построения решения задачи. Построено частное решение интегро-дифференциальной системы уравнений. Получены формулы для определения формы фронта ударной волны, поверхности обтекаемого тела, расстояния между ударной волной и поверхностью тела, параметров течения на поверхности крыла.

Ключевые слова: газовая динамика, гиперзвуковое обтекание тел, нестационарные течения, дифференциальные уравнения в частных производных, малый параметр.

Bogatko V.I.1, Potekhina E.A.2

1ORCID: 0000-0002-6247-6405, PhD in Physics and Mathematics, Associate professor, 2ORCID: 0000-0002-4307-3205, PhD in Physics and Mathematics, senior scientific researcher, St. Petersburg State University

ON ONE PARTICULAR SOLUTION OF THE PROBLEM OF SPATIAL HYPERSONIC FLOW PAST A VARIABLE FORM THIN WING

Abstract

The work is dedicated to the further study of the hypersonic gas flow past  a thin wing problem. The wing shape depends on the time. The resulting head shock wave is attached to the front edge of the wing, at least at one point. The solution is constructed using the thin shock layer method.. In determining the first order corrections two equations resulting system can be integrated independently of the others. Introduction of a new function and application of the Euler-Ampere transformation allows us to build a solution that depends on two arbitrary functions and unknown forms the front of the head shock wave. To determine these functions obtained integro-differential system of equations. In this paper we present one of variants of the semi-inverse method of constructing a solution in which a type of one of arbitrary functions is given. The shape of the streamlined body is defined in the process of constructing the solution of the problem. A particular solution of integro-differential equations of the system is built, The formulas for determining the shape of the shock front, the body surface, the distance between the shock wave and the body surface, the flow parameters on the wing surface were obtained.

Keywords: gas dynamics, hypersonic flow past bodies, unsteady flow, differential equations in partial derivatives, small parameter.

Введение

Для построения приближенного аналитического решения нелинейных задач чаще всего используют наличие малого параметра, который может присутствовать как в самой системе уравнений, так и в граничных условиях.

При обтекании тел гиперзвуковым потоком газа образуется сильная головная ударная волна. Задача состоит в определении параметров течения в области между головной ударной волной и обтекаемым телом. При этом форма головной ударной волны также подлежит определению.

Из условий, которые должны выполняться на головной ударной волне, в случае совершенного газа с постоянными теплоемкостями следует, что отношение плотностей на головной волне выражается формулой

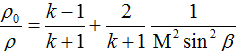
21-12-2016-10-01-36

где β - угол между наклоном головной ударной волны и направлением набегающего потока, M - число Маха, ρ0, ρ плотность газа до ударной волны и после соответственно, k - показатель адиабаты.

Первое слагаемое в правой части равно 21-12-2016-10-04-01 при k = 1,4  и при уменьшении показателя адиабаты будет уменьшаться. Таким образом, при больших скоростях будем иметь два малых параметра  21-12-2016-10-04-55. Заметим, что, как показывают расчеты, второе слагаемое с ростом скорости движения летательного аппарата убывает значительно быстрее первого.

Как показывают расчеты, влияние реальных свойств газа на аэродинамические параметры потока за фронтом ударной волны достаточно хорошо можно учесть уменьшением показателя адиабаты k [1]. При этом, если под k понимать эффективный показатель адиабаты, то уравнение состояния можно взять в квазисовершенном виде.

Метод разложения решения в ряды по степеням параметра ε (метод тонкого ударного слоя) был предложен Г.Г.Черным для решения двумерных задач (плоских стационарных и одномерных нестационарных) [2]. Хорошее совпадение результатов расчетов, полученных с помощью этого метода, с результатами численных расчетов и экспериментальными данными (см., например [2, 3]) позволяет сделать вывод о возможности его применения для приближенного решения задач газовой динамики с интенсивными ударными волнами вообще и задач обтекания в частности. При этом приемлемая для практических приложений точность решения может быть получена, если в разложении искомых функций в ряд ограничиться первыми двумя членами.

Отметим, что при использовании метода малого параметра обычно сохраняют члены одного порядка малости и в уравнениях, и в граничных условиях. Однако при решении задачи обтекания тела гиперзвуковым потоком газа методом тонного ударного слоя было обнаружено, что если записать граничные условия на фронте ударной волны, который соответствует предельному течению газа (т.е. при 21-12-2016-10-08-20), не производя дальнейших упрощений, и использовать для описания течения в ударном слое предельное решение уравнений газовой динамики, то построенное таким образом решение мало отличается от более точного решения, где и в уравнениях и в граничных условиях учтены все члены порядка ε [4]. Этот факт можно объяснить тем, что за фронтом сильной ударной волны основная масса газа в возмущенной области сосредотачивается  в узкой прифронтовой зоне, т.е. в ударном слое.

При учете конечности числа Маха набегающего потока для решения задач гиперзвукового обтекания параметры ε и η  чаще всего считаются независимыми [1]. В то же время известно, что с ростом скорости набегающего потока плотность газа за фронтом головной ударной волны растет, а величина эффективного показателя адиабаты уменьшается и вместе с уменьшением параметра η уменьшается и параметр ε. Из уравнения состояния следует, что параметр η  должен быть пропорционален ε, поэтому приближенно учесть конечность числа Маха набегающего потока можно положив 21-12-2016-10-11-10 [5].  Так как параметр η с ростом скорости движения тела убывает значительно быстрее, чем ε, то естественно считать l малой величиной.

Стационарный случай обтекания тонкого крыла был исследован в рамках метода тонкого ударного слоя в работах [6-8], позднее в [9,10] был предложен ряд частных решений, которые позволили для конкретных задач получить формулы для определения параметров течения на поверхности обтекаемого крыла.

Нестационарная задача обтекания гиперзвуковым потоком тонкого крыла переменной формы при 21-12-2016-10-12-04 исследовалась в [11]. Опираясь на результаты, полученные в [11], рассмотрим конкретный пример обтекания тонкого крыла переменной формы гиперзвуковым потоком совершенного газа.

Постановка задачи.

Задача состоит в определении параметров течения газа (u, v, w - компоненты вектора скорости частиц газа, p - давление, τ - величина, обратная плотности) за фронтом головной ударной волной, форма которого находится в процессе построения решения.

Толщина, размах и хорда крыла имеют порядок 21-12-2016-10-14-04 соответственно, при этом система координат 21-12-2016-10-14-31 выбирается таким образом, чтобы поверхность крыла мало отличается от плоскости 21-12-2016-10-15-03, а вектор скорости набегающего потока газа был параллелен плоскости 21-12-2016-10-15-31. Головная ударная волна считается присоединенной к передней кромке крыла по крайней мере в одной точке.

Решение системы нелинейных уравнений в частных производных, описывающей течение газа в возмущенной области строится методом тонкого ударного слоя. Решение должно удовлетворять граничным условиям динамической совместности на поверхности ударной волны и условию обтекания на поверхности крыла. Система уравнений для определения поправок первого приближения расщепляется, и два уравнения могут быть проинтегрированы независимо от остальных. Поскольку одно из этих уравнений может быть записано в дивергентном виде, вводится новая функция (аналог функции тока), что позволяет свести решение поставленной задачи к интегрированию одного нелинейного уравнения второго порядка в частных производных. Применение преобразования Эйлера-Ампера дает возможность построить решение, зависящее от двух произвольных функций и неизвестной формы фронта головной ударной волны, для определения которых получена интегро-дифференциальная система уравнений:

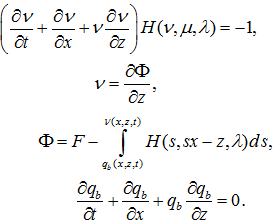21-12-2016-10-16-26  (1)

Здесь 21-12-2016-10-17-13  – уравнения поверхности крыла и формы фронта головной волны соответственно, H – произвольная функция, 21-12-2016-10-18-11 – функции, определяющие параметр q на поверхности головной ударной волны и на поверхности крыла соответственно, q = w – проекция скорости частиц газа на ось z (q = const на линиях тока), 21-12-2016-10-20-31.

Интегрирование системы (1) в общем случае для прямой задачи обтекания представляет значительные трудности. Предложенный в [11] полуобратный метод, состоящий в том, что вместо поверхности крыла задается вид функции H, позволяет не только построить решение системы (1), но и дополнительно задать уравнение передней кромки крыла, а в случае, когда головная волна присоединена вдоль всей передней кромки и наклон поверхности крыла на передней кромке. Форма обтекаемого крыла определяется в процессе построения решения задачи.

Частное решение задачи

Для того, чтобы построить частное решение задачи обтекания тонкого крыла переменной формы гиперзвуковым потоком газа вместо поверхности крыла зададим вид функции v:

21-12-2016-10-21-51  (2)

Тогда из первого уравнения системы (1) очевидно получаем 21-12-2016-10-22-31  (3)

Имея выражение (2), нетрудно проинтегрировать второе уравнение системы (1):

21-12-2016-10-23-22  (4)

Пусть для уравнения передней кромки крыла имеем: при  21-12-2016-10-24-10, тогда для присоединенной головной ударной волны из (4) получим:

21-12-2016-10-24-46 Отсюда очевидно 21-12-2016-10-25-26 и для формы фронта ударной волны окончательно получим 21-12-2016-10-26-12  (5)

После определения произвольных функций из граничных условий на передней кромке крыла, нетрудно получить решение последнего уравнения системы (1) в  параметрическом виде:

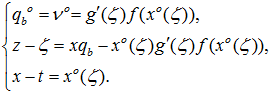21-12-2016-10-26-54  (6)

Здесь ζ – аппликата точки пересечения рассматриваемой линии тока с передней кромкой крыла.

Далее найдем расстояние между поверхностью крыла и фронтом ударной волны:

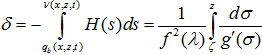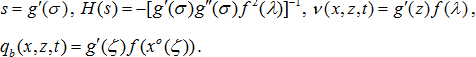
21-12-2016-10-28-55  (7) где 21-12-2016-10-29-56

Форма обтекаемой поверхности определяется затем из формулы

21-12-2016-10-33-58,  (8)

где для функций  21-12-2016-10-34-46  имеем формулы (5) и (7) соответственно.

Построенное решение интегро-дифференциальной системы уравнений позволяет теперь определить параметры течения на поверхности обтекаемого крыла.

Следуя [11], для  будем иметь

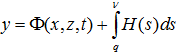21-12-2016-10-35-27   (9)

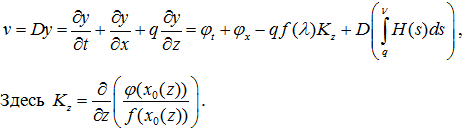Отсюда для составляющей вектора скорости получим 21-12-2016-10-36-15 На поверхности крыла при 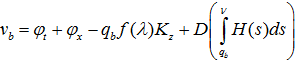21-12-2016-10-36-53  будем иметь 21-12-2016-10-37-28  (10)

Поправка к давлению и продольной компоненте вектора скорости определятся из уравнений, которые в переменных q, x, z, t имеют вид 21-12-2016-10-38-50

Заключение

Рассмотренное частное решение является модельным для различных режимов обтекания крыла. Кроме того он может быть использован для контроля результатов численных расчетов. Предлагаемый подход может быть также применен и при исследовании неравновесных течений (см., например, [12]).

В зависимости от специфики задачи может возникнуть необходимость использовать дополнительно различные варианты малых параметров. Они могут иметь отношение как к свойствам двигающегося газа или режимам его движения (слабая нестационарность потока, малая его запыленность и т.д.) [см., например, 13], так и к особенностям обтекаемой границы (например, слабая искривленность) [14]. Можно указать на возможность применения малого параметра, характеризующего время пребывания частицы газа в ударном слое. Для определения коэффициентов разложения получаются линейные алгебраические уравнения [15].

Список литературы / References

  1. Лунев В. В. Течения реальных газов с большими скоростями / В. В. Лунев – М.: ФИЗМАТЛИТ, 2007. – 760 с.
  2. Черный Г. Г. Течения газа с большой сверхзвуковой скоростью / Г. Г. Черный – М.: ФИЗМАТЛИТ, 1959. – 220 с.
  3. Hayes W. D., Probstein R. F. Hypersonic flow theory / W. D. Hayes, R. F. Probstein – New York and London, Acad. press, 1959. – 607 p.
  4. Su F. Y., Olfe D. B. Radiative transfere effects on reflected shock waves. I. Transparent gas / F. Y. Su, D. B. Olfe // Phys. Fluids. – 1971. Vol. 14. – N 12. – P. 2636 - 2644.
  5. Богатко В. И. К задаче нестационарного гиперзвукового обтекания клина и конуса / В. И. Богатко. // Прикладные вопросы аэрогазодинамики. – Киев.: Наукова думка, 1987. – С. 44-48.
  6. Messiter A. E. Lift of slender delta wings according to newtonian theory / A. E. Messiter // AIAA Journal. – 1963. -- Vol. 1. – N 4. – P. 1032-1034.
  7. Голубинский А. И., Голубкин В. Н. О пространственном обтекании тонкого крыла гиперзвуковым потоком газа / А. И. Голубинский, В. Н. Голубкин // Доклады АН СССР. – 1977. – Т. 234. – № 5. – С. 794-802.
  8. Богатко В. И., Гриб А. А., Колтон Г. А. Второе приближение в теории тонкого крыла конечного размаха, обтекаемого гиперзвуковым потоком газа / В. И. Богатко, А. А. Гриб, Г. А. Колтон // Вестник Ленинградского университета. – Серия 1. Математика. Механика. Астрономия. – 1979. – Вып. 1. – № 1. – С. 87-95.
  9. Богатко В. И., Колтон Г. А., Потехина Е. А. Полуобратный метод решения пространственной задачи обтекания тонкого крыла гиперзвуковым потоком газа / В. И. Богатко, Г. А. Колтон, Е. А. Потехина // Вестник Санкт-Петербургского государственного университета. – Серия 1. Математика. Механика. Астрономия. – 2015. Т. 2 (60). – Вып. 1. – С. 98-105.
  10. Bogatko, V. I., Potekhina, E. A., Kolton, G. A. An approach to solution of spatial hypersonic flow past a thin wing problem / V. I. Bogatko, E. A. Potekhina, G. A. Kolton // 2015 International Conference on Mechanics – Seventh Polyakhov's Reading 2015. DOI:10.1109/POLYAKHOV.2015. 7106717.
  11. Богатко В. И., Гриб А. А., Колтон Г. А. Обтекание тонкого крыла переменной формы гиперзвуковым потоком газа / В. И. Богатко, А. А. Гриб, Г. А. Колтон // Известия АН СССР. Механика жидкости и газа. – 1979. – № 4. – С. 94-101.
  12. Кузнецов М. М. О неравновесном обтекании тонкого крыла гиперзвуковым потоком газа / М. М. Кузнецов // Труды Центрального Аэрогидродинамического Института. – 1983. – Вып. 2177. – P. 77-95.
  13. Потехина Е. А. Метод тонкого ударного слоя в задаче о нестационарном обтекании клина и конуса гипрезвуковым потоком газа / Е. А. Потехина // Вестник Ленинградского университета. – Серия 1. Математика. Механика. Астрономия. – 1977. – № 7. – С. 117-123.
  14. Потехина Е. А., Селезнева И. Л. О нестационарном гиперзвуковом обтекании слабоизогнутого профиля / Е. А. Потехина, И. Л. Селезнева // Вестник Ленинградского университета. – Серия 1. Математика. Механика. Астрономия. – 1978. – № 13. – С. 103-108.
  15. Ильенко В. И., Потехина Е. А. К задаче о нестационарном обтекании плоского профиля / В. И. Ильенко, Е. А. Потехина // Вестник Ленинградского университета. – Серия 1. Математика. Механика. Астрономия. – 1980. – № 19. – С. 45-49.

Список литературы на английском языке / References in English

  1. Lunyov V. V. Techeniya real'nykh gazov s bol'shimi skorostyami [Flows of real gases at high speeds] / V. V. Lunev – M.: FIZMATLIT, 2007. – 760 p. [In Russian]
  2. Chyornyj G. G. Techeniya gaza s bol'shoy sverkhzvukovoy skorost'yu [Gas flows with a high supersonic velocity] / G. G. Chyornyj – M.: FIZMATLIT, 1959. – 220 p. [In Russian]
  3. Hayes W. D., Probstein R. F. Hypersonic flow theory / W. D. Hayes, R. F. Probstein – New York and London, Acad. Press. – 1959. – 607 p.
  4. Su F. Y., Olfe D. B. Radiative transfere effects on reflected shock waves. I. Transparent gas / F. Y. Su, D. B. Olfe // Phys. Fluids. – 1971. – Vol. 14. – N 12 – P. 2636 - 2644
  5. Bogatko V. I. K zadache nestatsionarnogo giperzvukovogo obtekaniya klina i konusa [On the problem of non-stationary hypersonic flow around a wedge and cone] / V. I. Bogatko. // Prikladnyye voprosy aerogazodinamiki. [Applied aerogasdynamics questions] – Kiev.: Naukova dumka, 1987. – P. 44-48. [In Russian]
  6. Messiter A.E. Lift of slender delta wings according to newtonian theory / A. E. Messiter // AIAA Journal. – 1963. -- Vol. 1. – N 4. – P. 1032-1034.
  7. Golubinskiy A. I., Golubkin V. N. O prostranstvennom obtekanii tonkogo kryla giperzvukovym potokom gaza [On a spatial hypersonic flow past a thin wing] / A. I. Golubinskiy, V. N. Golubkin // Doklady AN SSSR [Reports of the USSR Academy of Sciences]. – 1977. – Vol. 234. – N 5. – P. 794-802. [In Russian]
  8. Bogatko V. I., Grib A. A., Kolton G. A. Vtoroye priblizheniye v teorii tonkogo kryla konechnogo razmakha, obtekayemogo giperzvukovym potokom gaza [The second approximation in the theory of the finite span thin wing, streamlined by a hypersonic gas flow] / V. I. Bogatko, A. A. Grib, G. A. Kolton // Vestnik Leningradskogo universitetata. Seriya 1. Matematika.. Mekhanika. Astronomiya. [Bulletin of Leningrad University. – Series 1. Mathematics. Mechanics. Astronomy.] – 1979. – Iss. 1. – N 1. – P. 87-95. [In Russian]
  9. Bogatko V. I., Kolton G. A., Potekhina E. A. Poluobratnyy metod resheniya prostranstvennoy zadachi obtekaniya tonkogo kryla giperzvukovym potokom gaza [Semi-inverse method for solving the three-dimensional problem of flow around a thin wing hypersonic gas flow] / V. I. Bogatko, G. A. Kolton, E. A. Potekhina // Vestnik Sankt-Peterburgskogo gosudarstvennogo universiteta. – Seriya 1. Matematika.. Mekhanika. Astronomiya. [Bulletin of St. Petersburg State University. – Series 1. Mathematics. Mechanics. Astronomy.] – 2015. – Vol. 2 (60). – Iss. 1. – P. 98-105. [In Russian]
  10. Bogatko, V.I., Potekhina, E.A., Kolton, G.A. An approach to solution of spatial hypersonic flow past a thin wing problem / V. I. Bogatko, E. A. Potekhina, G. A. Kolton // 2015 International Conference on Mechanics – Seventh Polyakhov's Reading 2015. DOI: 10.1109/POLYAKHOV.2015.7106717 .
  11. Bogatko V. I., Grib A. A., Kolton G. A. Obtekaniye tonkogo kryla peremennoy formy giperzvukovym potokom gaza [Hypersonic gas flow past a thin wing of variable form] / V. I. Bogatko, A. A. Grib, G. A. Kolton // Izvestiya AN SSSR. Mekhanika zhidkosti i gaza. [Proceedings of the Academy of Sciences of the USSR. Fluid Mechanics] – 1979. – N 4. – P. 94-101. [In Russian]
  12. Kuznetsov M. M. O neravnovesnom obtekanii tonkogo kryla giperzvukovym potokom gaza [On the non-equilibrium hypersonic gas flow past a thin wing] / M. M. Kuznetsov // Trudy Tsentral'nogo Aerogidrodinamicheskogo Instituta [Proceedings of the Central Aero-Hydrodynamic Institute] – 1983. – Iss. 2177. – P. 77-95. [In Russian]
  13. Potekhina, E. A. Metod tonkogo udarnogo sloya v zadache o nestatsionarnom obtekanii klina i konusa giprezvukovym potokom gaza [Thin shock layer method in problem on an unsteady hypersonic flow past wedge and cone] / E. A. Potekhina // Vestnik Leningradskogo universitetata. Seriya 1. Matematika. Mekhanika. Astronomiya. [Bulletin of Leningrad University. – Series 1. Mathematics. Mechanics. Astronomy.] – 1977. – N 7. – P. 117-123. [In Russian]
  14. Potekhina E. A., Selezneva I. L. O nestatsionarnom giperzvukovom obtekanii slaboizognutogo profilya [Unsteady hypersonic flow past a weakly curved profile] / E. A. Potekhina, I. L. Selezneva // Vestnik Leningradskogo Universiteta. – Seriya Matematika Mekhanika Astronomiya. [Bulletin of Leningrad University. – Series 1. Mathematics. Mechanics. Astronomy.] – 1978. – N. 13. P. 103-108. [In Russian]
  15. Il'yenko V. I.; Potekhina E. A. K zadache o nestatsionarnom obtekanii ploskogo profilya. [On the problem of an unsteady hypersonic flow past plane profile.] / E. A. Potekhina, V. I. Il'yenko // Vestnik Leningradskogo Universiteta. – Seriya 1. Matematika Mekhanika Astronomiya. [Bulletin of Leningrad University – Series 1. Mathematics. Mechanics. Astronomy.] – 1980 – N. 19. – P. 45-49. [In Russian]