ОБ ОДНОЙ МОДЕЛИ ВЗАИМОДЕЙСТВИЯ ЛИТОСФЕРНЫХ СТРУКТУР

Телятников И.С.

ORCID: 0000-0001-8500-2133, Кандидат физико-математических наук,

Федеральный исследовательский центр «Южный научный центр Российской академии наук», Ростов-на-Дону, Россия

Исследование выполнено в рамках реализации ГЗ ЮНЦ РАН, проект № 01201354241 и при поддержке РФФИ и администрации Краснодарского края (проект 16-41-230184)

ОБ ОДНОЙ МОДЕЛИ ВЗАИМОДЕЙСТВИЯ ЛИТОСФЕРНЫХ СТРУКТУР

Аннотация

Получил развитие эффективный подход к исследованию напряженно-деформированного состояния литосферных структур, моделируемых системой пластин Кирхгофа на упругом слое, вблизи разломов. Реализован новый метод решения задачи, соответствующей модели прямолинейного разлома, в плоской постановке, проведены расчеты и проанализированы полученные результаты при варьировании физико-механических характеристик пластин и условий их контакта. Использование изложенного подхода позволит упростить алгоритм определения смещений покрытия и контактных напряжений, а также сделать выводы о влиянии типа разлома (граничных условий на стыке пластин) на характер волнового процесса в моделируемой геофизической среде, в частности изменение формы сигнала при прохождении через разлом, применимые для изучения характеристик разломов в верхней части коры Земли.

Ключевые слова: деформируемое основание, разлом, составное покрытие, вибрационная нагрузка, метод факторизации.

Telyatnikov I.S.

ORCID: 0000-0001-8500-2133, PhD in Physics and Mathematics,

Federal Research Centre «Southern Scientific Centre of Russian Academy of sciences», Rostov-on-Don, Russia

This work was carried out within the framework of the implementation of the State Order in SSC of RAS, project No. 01201354241 and supported by the Russian Fundamental Research Fund and the administration of the Krasnodar Krai (project 16-41-230184)

ON A MODEL OF INTERACTION OF LITHOSPHERIC STRUCTURES

Abstract

The paper presents the effective approach to the study of the stress-strain state of lithospheric structures simulated by the Kirchhoff plate system on the elastic layer near the splits. A new method for solving the problem corresponding to the rectilinear fault model was implemented in a flat setting, calculations were performed, and the obtained results were analyzed with varying physical and mechanical characteristics of the plates and the conditions for their contact. The use of this approach will simplify the algorithm for determining the displacements of the coating and contact stresses, and also draw conclusions about the effect of the fault type (boundary conditions at the plate interface) on the nature of the wave process in the simulated geophysical environment, in particular, the change in the shape of the signal when passing through a split, characteristics of splits in the upper part of the Earth's crust.

Keywords: deformable foundation, fault, composite coating, vibration load, factorization method.

В рамках основанных на применении концепции блоковой делимости литосферы моделей [1], [2] в настоящее время получены интересные результаты, характеризующие зарождения и развития сейсмических событий. Зачастую эпицентры землетрясений приурочены к границам блоков различных рангов [3]. Возможность возникновения землетрясения, вызванного концентрацией сейсмогенерирующих напряжений в области сближения и контакта литосферных структур и названного «стартовым», исследована в работе [4]. При этом в исследовании краевых задач для систем уравнений с частными производными (УЧП) использован метод блочного элемента, алгоритм которого изложен в [5], [6].

В работе развит эффективный подход к исследованию напряженно-деформированного состояния литосферных структур, моделируемых пластинами Кирхгофа на упругом основании, вблизи разломов. Реализован метод решения задачи, описывающей одну из моделей для случая прямолинейного разлома, в плоской постановке. Скалярный случай подобной задачи был рассмотрен автором в [7], при этом использован метод решения, связанный с преобразованием дифференциального оператора задачи. Предлагаемый в данной работе подход, основанный на упрощенном методе блочного элемента, является более универсальным в сравнении с [7] и одновременно обеспечивает получение более простых представлений решения задачи, чем топологический метод в [6, С. 16–18]. В результате численной реализации разработанного алгоритма проведены расчеты и проанализированы полученные результаты при варьировании физико-механических характеристик пластин и условий их контакта.

Рассматривается задача о вибрации двух занимающих полуплоскости контактирующих пластин на поверхности упругого основания под действием поверхностной сосредоточенной нагрузки . Декартова система координат связана со срединной плоскостью покрытия, ось  направлена по нормали вверх. В плоском случае установившийся процесс вертикальных колебаний пластин c частотой ω на упругом слое, жестко сцепленном с недеформируемым основанием, может быть описан с помощью линеаризованных уравнений [8, С. 27–28]

   (1)

где  – амплитуды перемещений и контактных напряжений на границе покрытия и подложки;

коэффициенты Пуассона,  – плотности,  – толщины пластин,  – модули Юнга их материалов. Здесь и далее использованы обозначения работы [7, С. 3], временной множитель  опущен.

Общий вид граничных условий на стыке частей покрытия, описанных в [8, С. 30–31], может быть представлен в следующей формулировке [7, С. 5]:

   (2)

Вид дифференциальных операторов  и определяется типом контактного взаимодействия пластин.

В рассматриваемой задаче соотношения для упругой подложки имеют вид [9, С. 26]

где  – амплитуды перемещений и напряжений на поверхности упругого слоя соответственно; функция Грина  упругого слоя с защемленной нижней гранью, содержащая в качестве параметров характеристики подложки: ν – коэффициент Пуассона, ρ – плотность, μ – модуль сдвига, h –толщину. Расположение в комплексной плоскости контура σ определяется принципом предельного поглощения [10, С. 101–108]. В трансформантах Фурье последнее соотношение можно записать

  (3)

где , – Фурье-образы функций  соответственно.

Условия сопряжения подложки с пластинами покрытия принимают вид: . Или в образах Фурье

   (4)

Общие решения уравнений (1), ограниченные на бесконечности в своих областях определения, найденные с учетом принципа предельного поглощения, имеют представление

где  – произвольные константы;  – вещественные положительные корни уравнений . Тогда для  справедливы представления

Применив с учетом принципа предельного поглощения к выражениям для  преобразование Фурье по соответствующим полупрямым, получим

   (5)

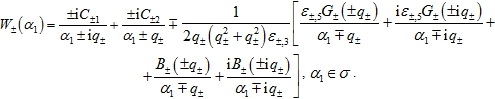
Из последнего соотношения можно выразить преобразования Фурье амплитуд контактных напряжений на нижних поверхностях пластин

  (6)

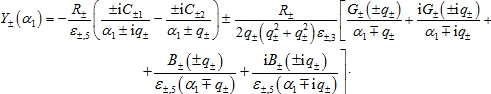
Из уравнения (1), соотношений для Фурье-образов перемещений и напряжений (3), а также условий контакта покрытия с подложкой (4) после ряда преобразований приходим к функциональному уравнению

   (7)

где 

В отличие от изложенного в [6] подхода предлагаемый в данной работе метод не требует преобразования оператора задачи и приводит к уравнению относительно интегральных характеристик контактных напряжений. Построенное функциональное уравнение (7) является нагруженным уравнением Винера – Хопфа в связи с наличием неизвестных , также подлежащих определению. Для этого в выражение  для  последовательно подставляются вместо  значения , а в выражение для . Таким образом, получается система алгебраических уравнений относительно , разрешив которую, остается подставить последние в выражения для трансформант Фурье перемещений (5).

Предлагаемый в данной работе алгоритм позволяет воспользоваться интегральным методом факторизации при решении (7), так как факторизуемые функции удовлетворяют условиям теорем, сформулированных в [10, С. 113–114].

Для факторизации по  относительно выбранного согласно принципу предельного поглощения контура σ функция  представляется в виде  [9, С. 61]. В качестве S используется функция . При этом параметр  выбирается достаточно большим [10, С.116–121], при численной реализации положено . Поведение  совпадает с поведением функции K на бесконечности, на вещественной оси у  нет особых точек. Особенности функции  совпадают с особенностями K, кроме того,  и она может быть приближена рациональной функцией  – соответственно вещественные нули и полюса функции K. Функции  в (7) имеют такое же поведение на бесконечности, как и K. Их полюса – нули  и полюса K. Тогда их можно представить как . Для каждого значения частоты ω функции  могут быть аппроксимированы с помощью полиномов Бернштейна [10, С. 124].

После подстановки найденных интегральных характеристик напряжений соотношения (5) будут содержать в качестве неизвестных только , определяемые из граничных условий в области стыковки пластин (2). Для этого к выражениям  применяется обратное преобразование Фурье для определения приближенных значений перемещений, которые следует подставить в граничные условия на стыке составляющих покрытия для получения амплитуд смещений поверхности.

Описанный подход позволяет исследовать зависимость характера прохождения сигнала от вида граничных условий в области контакта пластин, а также от свойств покрытия и основания. Результаты вычислительных экспериментов хорошо согласуются с полученными на основе подхода работы [7], что является свидетельством их достоверности, в то же время очевидное преимущество нового метода – отсутствие дополнительного преобразования дифференциального оператора задачи для последующего применения метода Винера – Хопфа.

Численная реализация разработанных алгоритмов позволила проанализировать результаты для некоторых задач при варьировании физико-механических характеристик покрытия и упругой подложки. На рисунках 1,2 представлены результаты модельных расчетов плоской задачи для безразмерной частоты , которая определялась как  ( – плотность,  – модуль сдвига правой пластины, a – характерный линейный размер), при этом выбраны безразмерные значения плотностей пластин и подложки , модуля сдвига упругого слоя , коэффициенты Пуассона . Вертикальная сосредоточенная нагрузка приложена в точке . На графиках по оси ординат отложена величина амплитуды вертикального смещения (линия красного цвета соответствует вещественной части комплексных амплитуд, зеленого – мнимой), по оси абсцисс - координата точки поверхности системы. Расчеты проведены для трех соотношений жесткостей пластин.

Рисунок 1 иллюстрирует амплитуды смещений поверхности слоя с составным покрытием для условия жесткого сцепления его частей

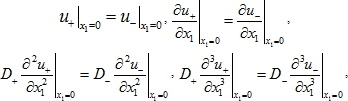
где 

Как видно из рис.1, с увеличение жесткости левой пластины амплитуды ее смещений уменьшаются. Тот же результат наблюдается для других типов условий контакта.

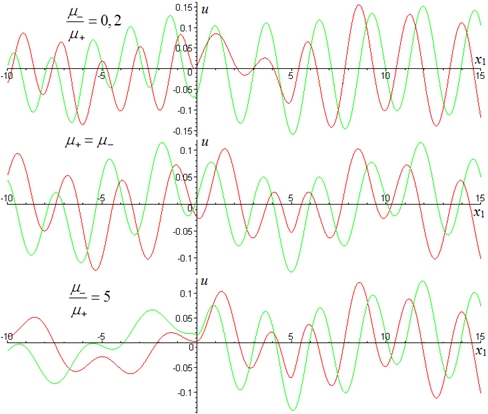
Рис. 1 – Комплексные амплитуды колебаний при жестком сцеплении пластин

 

На рис. 2 приведены результаты расчетов для случая свободно смещающихся пластин, т.е. когда в точке их контакта заданы условия равенства нулю изгибающих моментов и поперечных сил

Конфигурация гармонического сигнала изменяется (рис.2) при переходе через начало координат, т.е. точку стыковки элементов покрытия. Смещения терпят разрыв (скачок), амплитуда смещения менее жесткой пластины больше.

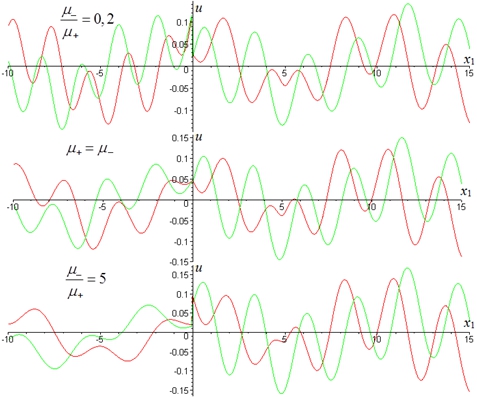
Рис. 2 – Комплексные амплитуды колебаний при свободном смещении пластин на стыке

 

Полученные результаты позволили выявить характер распространения гармонического сигнала в рассматриваемой структуре для однотипных и разнотипных элементов покрытия и различных условиях их контакта. Непосредственно на разломе определены конфигурации прохождения сигнала, которые могут служить для идентификации типа взаимодействия берегов разлома (свободное смещение, сцепление, контакт с трением и т. д.).

Развитие механико-математических методов идентификации разломов как сейсмогенерирующих зон в системе блоковой делимости земной коры на примере рассматриваемых моделей литосферных плит в виде системы контактирующих пластин Кирхгофа на поверхности деформируемой трехмерной подожки позволяет для криволинейных участков границ пластин строить кусочно-линейные аппроксимации, используя для каждого прямолинейного участка описанный в работе упрощенный подход.

Список литературы / References

1. Садовский М.А. Естественная кусковатость горной породы / М. А. Садовский // Доклады АН СССР. – 1979. – Т. 247, № 4. – С. 829–831.
2. Садовский М.А. Блоковая тектоника литосферы / М. А. Садовский, Л.И. Красный // Доклады АН СССР. – 1986. – Т. 287, № 6. – С. 1451–1454.
3. Oparin V.N. Gutenberg velocity section of the earth and its possible geomechanical explanation. I. Zonal disintegration and the hierarchical series of geoblocks / V. N. Oparin, M. V. Kurlenya // Journal of Mining Science. – 1994. – V. 30(2). – P. 97–108.
4. Babeshko V.A. Properties of «started» earthquakes / V.A. Babeshko, O.M. Babeshko, O.V. Evdokimova / Doklady Physics. – 2016. – V. 61, 4. – P. 188–191.
5. Babeshko V.A. The differential factorization method for a block structure / V.A. Babeshko // Doklady Physics. – 2009. – V. 54, Is. 1. – P. 25–28.
6. Block element method for body, localizations and resonances / Babeshko V.A. // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2014. – № 2. – С. 13–19.
7. Колесников М.Н. К методам исследования разломов в условиях вибрационных воздействий / М.Н. Колесников, И.С. Телятников // Научный журнал КубГАУ. – 2016. – № 121(07). – C. 647–659. http://ej.kubagro.ru/2016/07/pdf/33.pdf.
8. Вольмир А.С. Нелинейная динамика пластинок и оболочек / А.С.Вольмир. – М.: Наука, 1972. – 432 с.
9. Ворович И.И. Динамика массивных тел и резонансные явления в деформируемых средах / И.И. Ворович, В.А.Бабешко, О.Д. Пряхина. – М.: Научный мир, 1999. – 246 с.
10. Ворович И.И. Динамические смешанные задачи теории упругости для неклассических областей / И.И.Ворович, В.А. Бабешко. – М.: Наука, 1979. – 319 с.

Список литературы на английском языке / References in English

1. Sadovskiy M.A. Estestvennaja kuskovatost' gornoj porody [Natural lumpiness of rocks] // Doklady AS USSR [Proceedings of the USSR Academy of Sciences]. – 1979. – V. 247, № 4. – P. 829–831. [in Russian]
2. Sadovskiy M.A. Blokovaja tektonika litosfery [Block tectonics of lithosphere] / Sadovskiy M.A., Krasnyi L.I. // Doklady AS USSR [Proceedings of the USSR Academy of Sciences]. – 1986. – V. 287, № 6. P. 1451–1454. [in Russian]
3. Oparin V.N. Gutenberg velocity section of the earth and its possible geomechanical explanation. I. Zonal disintegration and the hierarchical series of geoblocks / V. N. Oparin, M. V. Kurlenya // Journal of Mining Science. – 1994. – V. 30(2). – P. 97–108.
4. Babeshko V.A. Properties of «started» earthquakes / V.A. Babeshko, O.M. Babeshko, O.V. Evdokimova / Doklady Physics. – 2016. – V. 61, Is. 4. – P. 188–191.
5. Babeshko V.A. The differential factorization method for a block structure / V.A. Babeshko // Doklady Physics. – 2009. – V. 54, Is. 1. – P. 25–28.
6. Block element method for body, localizations and resonances / Babeshko V.A. // EHkologicheskij vestnik nauchnyh centrov CHernomorskogo ehkonomicheskogo sotrudnichestva [Ecological Bulletin of Research Centers of the Black Sea Economic Cooperation]. – 2014. – № 2. – С. 13–19.
7. Kolesnikov M.N. K metodam issledovanija razlomov v uslovijah vibracionnyh vozdejstvij [To the research methods of faults under the vibration impacts] / M.N. Kolesnikov, I.S. Telyatnikov // Scientific Journal of KubSAU. – 2016. – V. 121(07). – P. 647–659. http://ej.kubagro.ru/2016/07/pdf/33.pdf. [in Russian]
8. Volmir A.S. Nelinejnaja dinamika plastinok i obolochek [Nonlinear Dynamics of Plates and Shells] / A.S. Volmir. – M.: Nauka, 1972. – 432 p. [in Russian]
9. Vorovich I.I. Dinamika massivnyh tel i rezonansnye javlenija v deformiruemyh sredah [Dynamic Behavior of Massive Bodies and Resonance Phenomena in Deformable Media] / I.I. Vorovich, V.A. Babeshko, O.D. Pryakhina. – М.: Nauchn. Mir, 1999. – 246 p. [in Russian]
10. Vorovich I.I. Dinamicheskie smeshannye zadachi teorii uprugosti dlja neklassicheskih oblastej [Dynamic mixed problem of elasticity theory for nonclassical domains]. / I.I. Vorovich, V.A. Babeshko. – M.: Nauka. 1979. – 319 p. [in Russian]