О РАСКРАШИВАЕМОСТИ ДВУДОЛЬНЫХ ГРАФОВ СПЕЦИАЛЬНОГО ВИДА
Магомедов А. М.
Доктор физико-математических наук, профессор, Дагестанский государственный университет
Работа выполнена при поддержке проекта № 2588 в рамках базовой части государственного задания Минобрнауки РФ и Отдела математики и информатики ДНЦ РАН
О РАСКРАШИВАЕМОСТИ ДВУДОЛЬНЫХ ГРАФОВ СПЕЦИАЛЬНОГО ВИДА
Аннотация
S. Asratyan и C.J. Casselgren доказали, что задача об интервальной реберной раскраске бирегулярного двудольного графа со степенями 6 и 3 соответственно («(6,3)-граф») NP-полна. В статье показано, что минимальная мощность n вершин, при которой (6,3)-граф не допускает раскраски требуемого вида, равна 18: любой (6,3)-граф с n<18 допускает интервальную реберную раскраску; для каждого n, не меньшего, чем 18 (и кратного 3), существует (6,3)-граф с n вершинами, для которого такая раскраска невозможна. Результаты находят применение в вопросах построения оптимальных расписаний учебных занятий.
Ключевые слова: граф, двудольный, раскраска.
Magomedov A.M.
PhD in Physics and Mathematics, Professor, Dagestan State University
THE COLORING OF SPECIAL KIND BIPARTITE GRAPHS
Abstract
S. Asratyan and C. J. Casselgren proved that the problem of the interval edge-coloring of biregular bipartite graph with degrees 6 and 3 respectively («(6,3)-graph») is NP-complete. The article shows that the minimum capacity of vertices n such that (6,3)-graph prevents coloring of the required form equal to 18: any (6,3)-graph with n<18 allows interval edge-coloring; for each n not less than 18 (and divided by 3) there is (6,3)-graph with n vertices, for which a coloring impossible. The results are used for constructing an optimal schedules training sessions.
Keywords: graph, bipartite, coloring.
- Введение
В статье использованы обозначения и определения из книги [1]. Интервальной реберной раскраской графа t цветами будем называть отображение множества ребер графа в множество ![]() , такое, что: 1) для каждого i,
, такое, что: 1) для каждого i, ![]() , найдется ребро, раскрашенное в цвет i, 2) в каждой вершине графа все представленные в ней цвета попарно различны и образуют целочисленный интервал.
, найдется ребро, раскрашенное в цвет i, 2) в каждой вершине графа все представленные в ней цвета попарно различны и образуют целочисленный интервал.
Двудольный граф ![]() в котором степени всех вершин X равны 6, а степени всех вершин Y равны 3, будем называть (6,3)-бирегулярным или, кратко, (6,3)-графом. При
в котором степени всех вершин X равны 6, а степени всех вершин Y равны 3, будем называть (6,3)-бирегулярным или, кратко, (6,3)-графом. При ![]() (6,3)-граф
(6,3)-граф ![]() будем называть
будем называть ![]() -графом. Будем называть (6,3)-граф раскрашиваемым или нераскрашиваемым в зависимости от того, допускает ли он интервальную реберную раскраску шестью цветами или нет.
-графом. Будем называть (6,3)-граф раскрашиваемым или нераскрашиваемым в зависимости от того, допускает ли он интервальную реберную раскраску шестью цветами или нет.
В [2] показана NP-полнота задачи о раскрашиваемости (6,3)-графа. Пример нераскрашиваемого ![]() –графа был построен еще в 1991 г. [3], в 2015 г. пример нераскрашиваемого
–графа был построен еще в 1991 г. [3], в 2015 г. пример нераскрашиваемого ![]() -графа опубликован в [4].
-графа опубликован в [4].
Сформулируем основной результат статьи.
Теорема 1. При ![]() каждый
каждый ![]() -граф раскрашиваем, для любого
-граф раскрашиваем, для любого ![]() найдется нераскрашиваемый
найдется нераскрашиваемый ![]() -граф.
-граф.
- Нераскрашиваемые
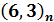 -графы
-графы
Отображение множества ребер E (6,3)-графа ![]() в множество из двух цветов, такое, что в каждой вершине
в множество из двух цветов, такое, что в каждой вершине ![]() цвета всех трех ребер, инцидентных y, одинаковы, а каждой вершине
цвета всех трех ребер, инцидентных y, одинаковы, а каждой вершине ![]() инцидентны три ребра каждого из двух цветов, будем называть гармонической раскраской графа G; значения цветов гармонической раскраски условимся обозначать -1 и + 1. Следующая лемма доказана независимо (и в разной терминологии) в [2] и [3].
инцидентны три ребра каждого из двух цветов, будем называть гармонической раскраской графа G; значения цветов гармонической раскраски условимся обозначать -1 и + 1. Следующая лемма доказана независимо (и в разной терминологии) в [2] и [3].
Лемма 1. Для раскрашиваемости (6,3)–графа G необходимо и достаточно существование гармонической раскраски графа G.
Нетрудно заметить беперспективность проверки существования нераскрашиваемого ![]() графа путем полного перебора даже при
графа путем полного перебора даже при ![]() Справедливость следующей леммы очевидна.
Справедливость следующей леммы очевидна.
Лемма 2. При гармонической раскраске (6,3)-графа для любой вершины ![]() сумма цветов ребер, инцидентных
сумма цветов ребер, инцидентных ![]() , равна нулю (свойство гармоничности для вершины
, равна нулю (свойство гармоничности для вершины ![]() ).
).
Следствие. При гармонической раскраске (6,3)-графа сумма цветов всех ребер графа равна нулю.
Двудольный граф ![]() , где
, где ![]() , а множество ребер
, а множество ребер ![]() задано списками смежности вершин множества
задано списками смежности вершин множества ![]() :
: ![]()
![]()
![]() , будем называть базисным.
, будем называть базисным.
Теорема 2. Если ![]() -граф
-граф ![]() является надграфом для базисного графа, то
является надграфом для базисного графа, то ![]() не допускает гармонической раскраски.
не допускает гармонической раскраски.
Доказательство. Допустим противное: пусть существует некоторая гармоническая раскраска ![]() графа
графа ![]() , являющегося надграфом для базисного графа. Цвет ребер, инцидентных вершине
, являющегося надграфом для базисного графа. Цвет ребер, инцидентных вершине ![]() , будем обозначать через
, будем обозначать через ![]()
![]() Выполнив почленное сложение равенств, выражающих свойство гармоничности для вершин
Выполнив почленное сложение равенств, выражающих свойство гармоничности для вершин ![]() соответственно:
соответственно:
![]()
![]()
![]()
получим: ![]() +2(
+2(![]()
Согласно следствию Леммы 2, ![]() . Отсюда
. Отсюда ![]() , что невозможно для
, что невозможно для ![]()
![]() . Полученное противоречие доказывает, что гармоническая раскраска графа
. Полученное противоречие доказывает, что гармоническая раскраска графа ![]() не существует. Теорема доказана.
не существует. Теорема доказана.
Пусть ![]() – целое положительное
– целое положительное ![]() . Любой двудольный граф
. Любой двудольный граф ![]() , где
, где ![]() ,
, ![]() , степени вершин:
, степени вершин:
![]() (1)
(1)
будем называть n–дополнением базисного графа или, кратко, n–дополнением.
В описанном ниже алгоритме построения n–дополнения текущие значения степеней вершин ![]() обозначены через
обозначены через ![]() , разности
, разности ![]() названы дефицитами вершин
названы дефицитами вершин ![]() , а вершины с дефицитами, равными нулю (отличными от нуля), названы насыщенными (соответственно – не насыщенными).
, а вершины с дефицитами, равными нулю (отличными от нуля), названы насыщенными (соответственно – не насыщенными).
Алгоритм 1. Построение n-дополнения
Вход: целое положительное ![]() списки со значениями элементов, заданными в (1):
списки со значениями элементов, заданными в (1): ![]() и
и ![]() .
.
Комментарии: элементы этих списков приобретут смысл степеней соответствующих вершин лишь после завершения алгоритма.
Выход: –дополнение для базисного графа.
- Инициализация:
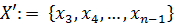 ;
; 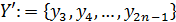 ;
; 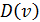 :=0 для всех
:=0 для всех 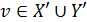 ;
;
Комментарии: после инициализации сумма дефицитов вершин каждого из множеств ![]() и
и ![]() равна
равна ![]() , а разность любых двух элементов следующего списка:
, а разность любых двух элементов следующего списка:
![]() (2)
(2)
равна -1, 0 или 1 («свойство близости элементов списка»).
- пока в множестве
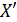 имеется ненасыщенная вершина
имеется ненасыщенная вершина 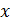 , соединить
, соединить 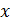 рёбрами с каждой из шести вершин множества
рёбрами с каждой из шести вершин множества 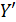 , имеющих наибольшие значения дефицитов.
, имеющих наибольшие значения дефицитов.
Комментарии: добавление ребра сопровождается увеличением текущих степеней его концевых вершин на единицу.
Конец алгоритма 1.
Справедливость следующей леммы очевидна.
Лемма 3. Для любого заданного целого положительного ![]() , алгоритм 1 генерирует n–дополнение
, алгоритм 1 генерирует n–дополнение ![]() .
.
Теорема 3. Для любого ![]() существует
существует ![]() -граф
-граф ![]() , не допускающий гармонической раскраски.
, не допускающий гармонической раскраски.
Доказательство. В качестве графа ![]() можно взять объединение базисного графа и его n–дополнения Теорема доказана.
можно взять объединение базисного графа и его n–дополнения Теорема доказана.
Следствие. Для любого ![]() существует 6-нераскрашиваемый
существует 6-нераскрашиваемый ![]() -граф
-граф ![]() .
.
В качестве примера 6-дополнения укажем граф ![]() , где
, где ![]() , а множество ребер
, а множество ребер ![]() задано списками смежности вершин множества
задано списками смежности вершин множества ![]() :
: ![]()
![]()
![]() .
.
Легко видеть, что граф ![]() , полученный объединением графов
, полученный объединением графов ![]() и
и ![]() , является
, является ![]() -графом. Согласно теореме 2,
-графом. Согласно теореме 2, ![]() не допускает гармонической раскраски, поэтому (по лемме 1) граф
не допускает гармонической раскраски, поэтому (по лемме 1) граф ![]() нераскрашиваем.
нераскрашиваем.
Мы доказали вторую часть теоремы 1. Первая часть теоремы 1 всецело получена «компьютерным» путем; изложим принятый нами подход. Для фиксированного n обозначим множество всех ![]() –графов через
–графов через ![]() . Ранее уже упоминалось о сложности полного перебора множества
. Ранее уже упоминалось о сложности полного перебора множества ![]() при
при ![]() проблема перебора сохраняет остроту и для
проблема перебора сохраняет остроту и для ![]() , хотя вычислительные трудности не столь велики, как в случае n=6.
, хотя вычислительные трудности не столь велики, как в случае n=6.
Наша цель – построить подмножество ![]() , такое, что утверждение о нераскрашиваемости всех
, такое, что утверждение о нераскрашиваемости всех ![]() –графов – элементов множества M – справедливо тогда и только тогда, когда аналогичное утверждение справедливо для всех элементов подмножества
–графов – элементов множества M – справедливо тогда и только тогда, когда аналогичное утверждение справедливо для всех элементов подмножества ![]() . Любое подмножество
. Любое подмножество ![]() , обладающее таким свойствами, будем называть характеристическим.
, обладающее таким свойствами, будем называть характеристическим.
Отношение изоморфизма разбивает множество ![]() на классы эквивалентности и, на первый взгляд, естественным представляется выбрать в качестве
на классы эквивалентности и, на первый взгляд, естественным представляется выбрать в качестве ![]() подмножество, включающее точно одного представителя из каждого класса эквивалентности. Однако такое построение затруднительно: задача об изоморфизме графов была опубликована [5] еще в 1972 г. как «открытая» задача, относительно которой неизвестно, является ли она NP-полной (насколько автору известно, за истекшие десятилетия успех в решении проблемы не достигнут). Поэтому ограничимся целью построить характеристическое множество
подмножество, включающее точно одного представителя из каждого класса эквивалентности. Однако такое построение затруднительно: задача об изоморфизме графов была опубликована [5] еще в 1972 г. как «открытая» задача, относительно которой неизвестно, является ли она NP-полной (насколько автору известно, за истекшие десятилетия успех в решении проблемы не достигнут). Поэтому ограничимся целью построить характеристическое множество ![]() , включающее столь мало представителей (но не менее одного) из каждого класса эквивалентности, что мощность
, включающее столь мало представителей (но не менее одного) из каждого класса эквивалентности, что мощность ![]() не будет представлять трудности для «компьютерного перебора».
не будет представлять трудности для «компьютерного перебора».
Введем обозначения: ![]()
![]() ,
, ![]()
![]() ;
;
![]() ,
, ![]()
Построение множества ![]() удобно изложить в виде построения корневого дерева
удобно изложить в виде построения корневого дерева ![]() глубины
глубины ![]() , все узлы которого представлены двудольными графами (далее в тексте – «узловые графы»), а узловые графы, представляющие узлы последнего,
, все узлы которого представлены двудольными графами (далее в тексте – «узловые графы»), а узловые графы, представляющие узлы последнего, ![]() -го уровня, являются
-го уровня, являются ![]() –графами и образуют множество
–графами и образуют множество ![]() ; при этом каждый узел
; при этом каждый узел ![]() уровня
уровня ![]() , принадлежащий пути от корня к некоторой вершине
, принадлежащий пути от корня к некоторой вершине ![]() последнего уровня
последнего уровня ![]() , будет представлен некоторым порожденным на множестве вершин
, будет представлен некоторым порожденным на множестве вершин ![]() подграфом
подграфом ![]() =
= ![]() графа
графа ![]() .
.
Алгоритм 2. Построение характеристического множества
Вход: целое положительное ![]() .
.
Выход: «слабо-избыточное» характеристическое множество ![]() – множество узловых графов последнего уровня дерева
– множество узловых графов последнего уровня дерева ![]() .
.
- В качестве узлового графа для узла 0-го уровня (корня дерева
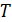 ) выбрать двудольный граф
) выбрать двудольный граф 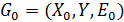 , где
, где 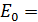

![]() (
( ![]() – количество узлов в дереве
– количество узлов в дереве ![]() ).
).
- Для каждого
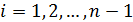 выполнить:
выполнить:
для узлового графа ![]() =
=![]() каждого узла
каждого узла ![]() уровня
уровня ![]() выполнить:
выполнить:
Begin_1
2.1. Разбить множество Y графа ![]() на поля, где каждое поле представляет собой набор всех таких вершин степени <3, которые обладают одним и тем же списком смежности. Количество полей обозначить через N, поля – через
на поля, где каждое поле представляет собой набор всех таких вершин степени <3, которые обладают одним и тем же списком смежности. Количество полей обозначить через N, поля – через ![]() , их мощности – через
, их мощности – через ![]() индексы первых элементов полей – через
индексы первых элементов полей – через ![]()
2.2. Для каждого неупорядоченного набора целых неотрицательных ![]() , удовлетворяющих условиям:
, удовлетворяющих условиям:
![]() и
и ![]()
выполнить:
Begin_2
2.2.1. ![]() двудольный граф, полученный из
двудольный граф, полученный из ![]() добавлением вершины
добавлением вершины ![]() , список смежности которого содержит точно
, список смежности которого содержит точно ![]() начальных вершин поля
начальных вершин поля ![]() ,
, ![]() ;
;
2.2.1.1. если а) список смежности вершины ![]() в графе
в графе ![]() содержит не более общих вершин с
содержит не более общих вершин с ![]() , чем список смежности вершины
, чем список смежности вершины ![]() в
в ![]() и
б) граф
и
б) граф ![]() содержит
содержит ![]() вершин множества Y, степени которых < 3,
вершин множества Y, степени которых < 3,
то
добавить ![]() в дерево
в дерево ![]() в качестве потомка вершины
в качестве потомка вершины ![]() , для чего:
, для чего:
![]() и узлу с номером
и узлу с номером ![]() приписать граф
приписать граф ![]() (в подробной компьютерной реализации рекомендуется выполнить и следующие действия сопроводительного характера: в соответствующие массивы занести с позиции
(в подробной компьютерной реализации рекомендуется выполнить и следующие действия сопроводительного характера: в соответствующие массивы занести с позиции ![]() значения
значения ![]() , N, номер родительского узла
, N, номер родительского узла ![]() и векторы
и векторы ![]() ,
, ![]() и
и ![]() ).
).
End_2
End_1
Конец алгоритма 2.
Заметим, что ![]() не принимают видимого участия в алгоритме, но их присутствие оправдано вычислительными целями (для удобства вычисления полей узла-потомка).
не принимают видимого участия в алгоритме, но их присутствие оправдано вычислительными целями (для удобства вычисления полей узла-потомка).
Для генерации наборов целых неотрицательных ![]() , удовлетворяющих условиям (*), применяется рекурсивная процедура AddSplit (
, удовлетворяющих условиям (*), применяется рекурсивная процедура AddSplit ( ![]() , где
, где ![]() и
и ![]() – векторы из N целых неотрицательных и целых положительных чисел соответственно: по заданным
– векторы из N целых неотрицательных и целых положительных чисел соответственно: по заданным ![]() и
и ![]() процедура генерирует все разбиения заданного целого положительного
процедура генерирует все разбиения заданного целого положительного ![]() на неупорядоченные целые неотрицательные слагаемые:
на неупорядоченные целые неотрицательные слагаемые: ![]()
![]() не превышающие соответствующие
не превышающие соответствующие ![]() . Процедура содержит вложенный вызов процедуры AddVertex, действие которой равносильно выполнению фрагмента Begin_2 … End_2 алгоритма 2 по добавлению в дерево
. Процедура содержит вложенный вызов процедуры AddVertex, действие которой равносильно выполнению фрагмента Begin_2 … End_2 алгоритма 2 по добавлению в дерево ![]() нового узла – потомка узла
нового узла – потомка узла ![]() . Приведем подробное описание.
. Приведем подробное описание.
Процедура AddSplit (![]() )
)
Если ![]() , то begin
, то begin ![]() :=value; AddVertex end
:=value; AddVertex end
иначе
для ![]() от
от ![]() (
( ![]() ) до
) до ![]() (
( ![]() ,
, ![]() ) выполнить:
) выполнить:
Begin_1 ![]() ; AddSplit (
; AddSplit (![]() ) End_1
) End_1
Комментарии: перед вызовом процедуры выполняются присваивания: ![]() и
и ![]() .
.
Конец процедуры
Как видно из описания процедуры, память на хранение наборов ![]() , удовлетворяющих условиям (*), не расходуется: для каждого очередного набора немедленно после его генерации выполняется фрагмент Begin_2 … End_2.
, удовлетворяющих условиям (*), не расходуется: для каждого очередного набора немедленно после его генерации выполняется фрагмент Begin_2 … End_2.
Теорема 4. Алгоритм 2 вычисляет характеристическое множество.
Доказательство. Требуется показать, что для каждого ![]() –графа – элемента множества
–графа – элемента множества ![]() – среди узловых графов последнего уровня дерева
– среди узловых графов последнего уровня дерева ![]() найдется изоморфный ему граф (назовем это условие кратко: принцип достаточности). Отличия алгоритма 2 от алгоритма полного перебора начинаются с выбора (в пункте 1) единственного узлового графа для корня, остальные отличия сводятся к выбору (в пункте 2.2.1.1) не более одного потомка для узла
найдется изоморфный ему граф (назовем это условие кратко: принцип достаточности). Отличия алгоритма 2 от алгоритма полного перебора начинаются с выбора (в пункте 1) единственного узлового графа для корня, остальные отличия сводятся к выбору (в пункте 2.2.1.1) не более одного потомка для узла ![]() уровня
уровня ![]() из каждого множества графов, соответствующего сгенерированному разбиению
из каждого множества графов, соответствующего сгенерированному разбиению ![]() числа 6 на целые положительные слагаемые.
числа 6 на целые положительные слагаемые.
Во-первых, выбор для вершины ![]() любого иного списка смежности приводит к графу, изоморфному
любого иного списка смежности приводит к графу, изоморфному ![]() . В самом деле, пусть для вершины
. В самом деле, пусть для вершины ![]() выбран произвольный список смежности
выбран произвольный список смежности ![]() . Тогда любая биекция {
. Тогда любая биекция {![]() }
} ![]() приводит к (изоморфному) графу
приводит к (изоморфному) графу ![]() с сохранением принципа достаточности.
с сохранением принципа достаточности.
Во-вторых, требование (см. 2.2.1.1а) «список смежности вершины ![]() в графе
в графе ![]() имеет не более общих вершин с
имеет не более общих вершин с ![]() , чем список смежности вершины
, чем список смежности вершины ![]() в
в ![]() » равносильно требованию упорядочить вершины
» равносильно требованию упорядочить вершины ![]() по принципу невозрастания в их списках смежности количеств вершин, принадлежащих
по принципу невозрастания в их списках смежности количеств вершин, принадлежащих ![]() ; такое упорядочение соответствует принципу достаточности. Наконец, если (см. 2.2.1.1б) граф
; такое упорядочение соответствует принципу достаточности. Наконец, если (см. 2.2.1.1б) граф ![]() содержит менее шести вершин множества Y степени меньше, чем три, то, очевидно, достроить граф
содержит менее шести вершин множества Y степени меньше, чем три, то, очевидно, достроить граф ![]() до
до ![]() –графа невозможно. Теорема доказана.
–графа невозможно. Теорема доказана.
Как показали компьютерные расчеты, при ![]() алгоритм 2 генерирует дерево
алгоритм 2 генерирует дерево ![]() из 11645 узлов, из которых 2485 узлов относятся к последнему уровню, образуя искомое множество
из 11645 узлов, из которых 2485 узлов относятся к последнему уровню, образуя искомое множество ![]()
![]() графов. Проверка существования гармонической раскраски у каждого графа из
графов. Проверка существования гармонической раскраски у каждого графа из ![]() путем обычного перебора не представляет трудности; среди них обнаружены точно 62 нераскрашиваемых графа (в том числе – изоморфные между собой), включая рассмотренный выше граф
путем обычного перебора не представляет трудности; среди них обнаружены точно 62 нераскрашиваемых графа (в том числе – изоморфные между собой), включая рассмотренный выше граф ![]() . Для каждого
. Для каждого ![]() компьютерные расчеты подтвердили существование гармонической раскраски у всех графов характеристического множества, следовательно, их раскрашиваемость (лемма 1). Тем самым доказано и первое утверждение теоремы 1.
компьютерные расчеты подтвердили существование гармонической раскраски у всех графов характеристического множества, следовательно, их раскрашиваемость (лемма 1). Тем самым доказано и первое утверждение теоремы 1.
- Заключение
Область практического применения – построение «безоконного» расписания. Пусть рассматривается задача построения однодневного расписания учебных занятий: – множество классов, – множество учителей, исходные данные к расписанию заданы (6,3)-графом ![]() , где каждому классу запланированы шесть уроков, а каждому учителю – три урока. Если цвету
, где каждому классу запланированы шесть уроков, а каждому учителю – три урока. Если цвету ![]() каждого ребра (
каждого ребра (![]() соотнести номер академического часа – урока учителя
соотнести номер академического часа – урока учителя ![]() в классе
в классе ![]() , то задача о раскрашиваемости графа
, то задача о раскрашиваемости графа ![]() преобразуется в задачу о существовании расписания длительностью в шесть уроков без «окон» у учителей и классов.
преобразуется в задачу о существовании расписания длительностью в шесть уроков без «окон» у учителей и классов.
Литература
- Swamy M. N. and Thulasiraman K. Graphs, Networks and Algorithms, Wiley-Inter-science, 1981. – 455 P.
- Casselgren C. J. On Some Graph Coloring Problems // Doctoral Thesis No. 48. Department of Mathematics and Mathematical Statistics Umea University, 2011.
- Магомедов А. М. К вопросу об условиях уплотнимости матрицы из 6 столбцов // Деп. в ВИНИТИ, 1991.
- Magomedov A. M. On interval -coloring bipartite graphs // ISSN 0005-1179, Automation and Remote Control, 2015, Vol. 76, No. 1, pp. 80–87.
- Karp R. M. Reducibility among combinatorial problems // in R. E. Miller and J. W. Thatcher (eds.), Complexity of Computer Computations, Plenum Press, New York, 1972. P. 85-103.
References
- Swamy M. N. and Thulasiraman K. Graphs, Networks and Algorithms, Wiley-Inter-science, 1981. – 455 P.
- Casselgren C. J. On Some Graph Coloring Problems // Doctoral Thesis No. 48. Department of Mathematics and Mathematical Statistics Umea University, 2011.
- Magomedov A. M. K voprosu ob uslovijah uplotnimosti matricy iz 6 stolbcov // Dep. v VINITI, 1991.
- Magomedov A. M. On interval -coloring bipartite graphs // ISSN 0005-1179, Automation and Remote Control, 2015, Vol. 76, No. 1, pp. 80–87.
- Karp R. M. Reducibility among combinatorial problems // in R. E. Miller and J. W. Thatcher (eds.), Complexity of Computer Computations, Plenum Press, New York, 1972. P. 85-103.
