О МЕХАНИЗМЕ ФОРМИРОВАНИЯ ЛИНИЙ ЩЕЛОЧНЫХ МЕТАЛЛОВ В СПЕКТРАХ СОНОЛЮМИНЕСЦЕНЦИИ
О МЕХАНИЗМЕ ФОРМИРОВАНИЯ ЛИНИЙ ЩЕЛОЧНЫХ МЕТАЛЛОВ В СПЕКТРАХ СОНОЛЮМИНЕСЦЕНЦИИ
Научная статья
Казачек М.В.1, Гордейчук Т.В.2, * 1 ORCID: 0000-0001-9320-1124; 2 ORCID: 0000-0001-8425-4080; 1, 2 Тихоокеанский океанологический институт им. В.И. Ильичева, Владивосток, Россия
* Корреспондирующий автор (Tanya[at]poi.dvo.ru)
Аннотация Представлен доработанный вариант модели формирования линий щелочных металлов в спектрах сонолюминесценции. Модель основана на гипотезе, что сложный профиль линий является результатом наложения спектров, излученных при различной плотности возмущающей среды, и успешно объясняет все особенности линии. Рассмотрено поведение модели при варьировании ее параметров. Рассмотрены варианты модели: при аппроксимации формы линии гауссовой, лоренцевой, треугольной функциями; для различного вида зависимости плотности от времени; с учетом зависимости интенсивности излучения металла от времени. В рамках модели обработан большой массив экспериментальных спектров Na, K, Li, произведены оценки диапазонов плотности, при которой происходит излучение металлов, вклада различных компонентов излучения в спектры. Модель позволяет существенно продвинуться в понимании механизма излучения металлов при сонолюминесценции. Ключевые слова: сонолюминесценция, атомная эмиссия щелочных металлов, форма спектральной линии.ON MECHANISM OF ALKALI METALS LINES FORMATION IN SONOLUMINESCENCE SPECTRA
Research Article
Kazachek M.V.1, Gordeychuk T.V.2, * 1 ORCID: 0000-0001-9320-1124; 2 ORCID: 0000-0001-8425-4080; 1, 2 Il’ichev Pacific Oceanological Institute, Vladivostok, Russia
* Corresponding author (Tanya[at]poi.dvo.ru)
Abstract A modified version of the alkali metal line formation model in the sonoluminescence spectra is presented in the paper. The model is based on the hypothesis that the complex profile of lines is the result of superposition of the spectra emitted at different densities of the disturbing medium, and successfully explains all the features of the line. The behavior of the model with its varying parameters is considered. The following options of the model are considered: when approximating the line shape of a Gaussian, Lorentzian, triangular functions; for various types of dependence of density on time; considering the dependence of the intensity of metal radiation on time. Within the framework of the model, a large array of experimental spectra of Na, K, Li is processed. The authors estimate density ranges at which metals are emitted and the contribution of various radiation components to the spectra occurs. The model makes significant progress in understanding the mechanism of metal radiation in sonoluminescence. Keywords: sonoluminescence, alkali metal atomic emission, spectral line shape.Сонолюминесценцией (СЛ) называют слабое световое излучение, сопровождающее ультразвуковую кавитацию в жидкостях. Для объяснения СЛ наиболее приемлемой считается гипотеза «горячего пятна» («hot-spot») [1], согласно которой нелинейные пульсации парогазовых пузырьков сопровождаются формированием внутри них пиковых температур и давлений в тысячи кельвинов и сотни атмосфер. Экстремальные условия обуславливают формирование большого разнообразия возбужденных состояний частиц. Оптические спектры многопузырьковой СЛ водных растворов содержат широкий континуум, источник которого относят к тормозному излучению, излучению черного тела и молекулярной эмиссии возбужденных состояний [2]. В спектрах водных растворов соединений щелочных металлов содержатся линии, соответствующие возбужденным состояниям атомов металлов. Эти линии обладают рядом особенностей [3], [4], [5], [6]. Они состоят из асимметричной широкой компоненты с центром, сдвинутым в длинноволновую область относительно спектра в пламени. На широкую компоненту налагается узкая компонента, соответствующая линиям в пламени. Широкую компоненту объясняют плотностным уширением [7], [8], что свидетельствует об излучении из сильно сжатой газовой фазы изнутри пузырька. Происхождение узкой несмещенной компоненты, излучение которой возможно только при низкой плотности среды, порядка плотности при нормальном давлении, остается неясным.
Мы исследовали механизм формирования линий металлов при СЛ на примере D-линии Na. Мы предположили, что причиной асимметричной сдвинутой формы широкой компоненты является ее интегральный характер, когда в процессе пузырькового коллапса, происходит наложение спектров, излученных при различной плотности возмущающей среды. Эта гипотеза легла в основу простой модели [4], которая позволяет успешно симулировать форму экспериментальных спектров, объясняя все особенности профиля линий (ширину, асимметрию, сдвиг, наличие узкой компоненты). Отметим, что то обстоятельство, что излучение металлов занимает значительный диапазон плотностей, получило экспериментальное и теоретическое подтверждение [9, 10]. В данной работе приведен усовершенствованный алгоритм модели. Модель позволила оценить верхний и нижний порог плотности фазы излучения металла, характер временной зависимости плотности в течение этой фазы и вклад узкой компоненты в излучение по форме линий щелочных металлов в экспериментальных спектрах СЛ. Подробное описание экспериментальной установки и процедуры измерения спектров изложено ранее [2], [4], [5], [7]. При разработке модели в качестве экспериментального спектра использовали линию Na в спектре многопузырьковой СЛ высокого разрешения (0.26 нм, ширина щели монохроматора 0.2 мм) водного раствора NaCl, насыщенного аргоном. Частота ультразвука составляла 22 кГц, общая поглощенная ультразвуковая мощность 40 Вт. Спектры измеряли вблизи линии Na при различных температуре 5-15 ºС, концентрации 0.5-4 М и гидростатическом давлении 1-2 атм. Существенных изменений формы D-линии Na в исследованном диапазоне экспериментальных условий замечено не было. В работе также приводятся результаты моделирования линий K, Na, Li в спектрах многопузырьковой СЛ 3 М водных растворов КCl, NaCl, LiCl, насыщенных аргоном. Спектры измеряли вблизи линий металлов для частоты 20 кГц и общей поглощенной ультразвуковой мощности 20 Вт. Линии металлов в пламени с добавлением соответствующих солей, представленные в работе для сравнения, измеряли при том же разрешении спектрометра, что и спектры СЛ. Спектры СЛ 2 М водного раствора NaCl и 5 мМ водного раствора SDS (sodium dodecyl sulfate) измеряли для частоты ультразвука 20 и 870 кГц. Общая поглощенная мощность для частоты 870 кГц составляла 5 Вт. Температура растворов поддерживалась равной 10 ºС. Все спектры измерены методом сканирования на монохроматоре МДР-23 с использованием фотоумножителя ФЭУ-79.
На рисунке 1 показаны ход радиуса и температуры для классической модели пузырька вблизи момента пика коллапса tp, взятые из [8], а также ход плотности, вычисленный нами по кривой радиуса в допущении, что временной интервал мал для процесса массообмена пузырек-жидкость. Плотность и температура внутри пузырька сохраняют высокие значения в течение нескольких нс вблизи момента tp (рис.1). Длительность вспышки для однопузырьковой СЛ в воде, насыщенной аргоном, составляет ~0,15 нс [11], в дегазированной воде ~1,9 нс [12]. Длительность вспышки многопузырьковой СЛ ~ 1 нс [13]. Длительность вспышки резонансной радиации Na составляет~10-70 нс [12], т.е. превышает временной интервал высокоплотной фазы коллапса. В работе [9] экспериментально показано, что свечение Na в пузырьке, образованном вспышкой лазера, зарегистрированное с применением фильтра с полосой пропускания 585-595 нм, начинается за десятки нс и проходит максимум до вспышки континуума в диапазоне 250-450 нм. Эти данные подтверждают различие временных фаз излучения континуума и металлов во время СЛ.
Оценим, исходя из приведенных на рисунке 1 зависимостей, пиковую плотность в пузырьке np. На конечной фазе сжатия процесс приближается к адиабатическому, температура и плотность резко возрастают. Согласно [8], для пузырька, колеблющегося в ультразвуковом поле частотой 26.5 кГц, это происходит за ~20 нс до момента tр. Допустим, что в момент (tр - 20) нс плотность содержимого пузырька еще близка к нормальной, т.е. n0~1 Амг (1 Амг=2.6868·1019 см-3). Радиус пузырька уменьшается от R0 ~8 мкм до Rp ~0.8 мкм. Тогда из соотношения np/n0=(R0/Rp)3 получаем значение np~1000 Амг. Отметим, что плотность воды при нормальных условиях составляет ~1240 Амг, т.е. пиковая плотность в пузырьке может приближаться к плотности жидкости.
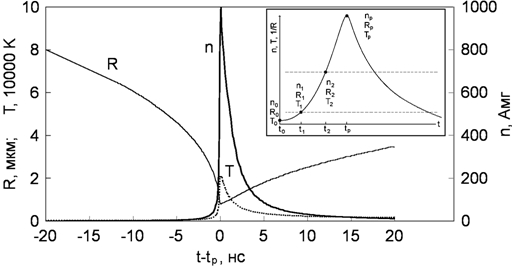
Рис. 1 – Расчетный ход радиуса R, температуры T [8] и плотности n (рассчитан по кривой R) вблизи коллапса для пузырька, подверженного колебаниям в ультразвуковом поле частотой 26.5 кГц
На врезке показана схематическая зависимость плотности n, обратного радиуса 1/R и температуры T от времени t: момент t0 - низкая плотность, равновесный радиус, низкая температура; момент t1 - начало свечения Na; момент t2 - конец свечения Na; момент tр - пиковые значения величин. Область между штриховыми линиями - зона свечения металла. Для оценки плотности n1, при которой металл начинает излучать, используем соотношения T1/T0=(R0/R1)3(Г-1), n1/n0=(R0/R1)3. Здесь R1, T1, n1 - значения радиуса пузырька, температуры и плотности среды в момент начала эмиссии, соответственно; R0, T0, n0 - их значения в некоторый момент, предшествующий адиабатическому сжатию (врезка к рис.1), Г - показатель политропы. Мы полагаем, что для смеси паров воды и аргона значение Г=1.5. Тогда плотность n1, которая соответствует повышению температуры внутри пузырька от T0~300 K до T1~1400 K (положим, что это температура начала излучения), составит ~20 Амг. Допустим, что излучение Na может происходить до некоторой плотности n2 np. Заметим, что с точки зрения модели, факт высвечивания металла на фазе сжатия или расширения (до или после момента tp) является равновероятным.
Ширина (FWHM, full width at half maximum) экспериментальной линии Na, (~3 нм, рис. 2) и коэффициент уширения g для Na в Ar [14] позволяют оценить некоторую среднюю плотность в течение эмиссии n~125 Амг. Предложенные в [7], [15] оценки другими способами составили 60 и 70 Амг, соответственно. Давление можно оценить из известного соотношения P=nkT. Для Т=2000 К и n=125 Амг получаем Р~920 атм, что соответствует оценке пикового давления кавитации, сделанной нами ранее [7]. Заметим, что для значений g, приведенных в [14], и np~1000 Амг в случае линии Na FWHM должна была составить ~22 нм, что значительно превышает ширину экспериментальной линии.
Оценка плотности прямо зависит от значений коэффициентов сдвига s и уширения g, которые точно не определены по следующим причинам - высокие значения плотности, для которых коэффициенты не изучались, неизвестный состав возмущающего вещества, неизвестная зависимость s и g от температуры. Если предположить, что Na светится в пограничном слое [16], то возмущающим веществом будет преимущественно вода. Этим можно объяснить отсутствие влияния типа насыщающего газа на ширину и сдвиг линии, отмеченное в [17], и иное, чем для аргона, отношение s/g, получаемое в нашей модели. Независимость формы линии от давления насыщенного пара растворителя может быть связана с тем, что в [17] исследован ряд однородных растворителей (спирты), для которых s/g могут быть близки, а пиковые плотности по какой-либо причине не влияют на спектр.
Согласно обзору [14], зависимость сдвига и уширения спектральных линий щелочных металлов инертными газами от плотности близка к линейной. Положение линии Λ и её полуширину S представим в виде:
Λ(n)=Λ0+s·s·n, S(n)=S0+g·n, (1)
где Λ0 и S0 - длина волны и полуширина на полувысоте (HWHM, half width at half maximum) при плотности n0=1 Амг, s и g - коэффициенты сдвига и уширения для каждой линии, соответственно, s - добавочный множитель к s. Мы используем s в качестве параметра, для коэффициентов s и g мы используем значения [14].
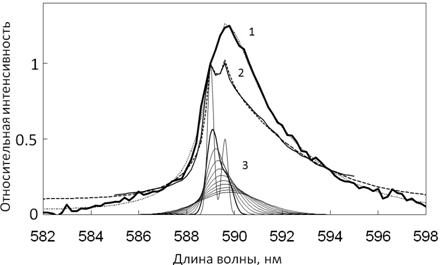
Рис. 2 – Кривые 1 и 2 – D-линии Na в экспериментальных спектрах СЛ водного раствора NaCl для частот 22 кГц (наш спектр) и 138 кГц [15] (сплошные линии) и их модели, рассчитанные по формуле (5) (пунктирные линии)
Спектры нормированы на длине волны первого компонента дублета. Параметры моделей, полученные наилучшим заполнением экспериментальной кривой, приведены в таблице 2. Семейство кривых 3 - модельные спектры, рассчитанные по формуле (2), иллюстрируют эволюцию формы линии при уширении одной плотностью с диапазоне от 0 до 100 Амг с шагом 10 Амг (нормированы по площади). Жирная линия соответствует плотности n=10 Амг
Внутри пузырька при максимальном сжатии содержится в основном аргон (86% Ar и 14% H2O [18]), поэтому мы рассматриваем взаимодействие Na и Ar. Коэффициенты сдвига s и полуширины g для Na в Ar [14] сведены в таблицу 1. Эти коэффициенты определены для температуры порядка ~400-600 K, тогда как пиковая температура многопузырьковой СЛ значительно выше и имеет порядок ~2000-5000 K [19]. Кроме того, в пузырьке, кроме Na и Ar, присутствуют пары воды и продукты ее диссоциации. Однако в первом приближении можно принять, что возмущение другой частицей равно возмущению аргоном. В [15] для оценки пиковой плотности использовали коэффициент уширения линии Na в Ar g=3.31·10-20 см-1/см-3 для Т=2000 К. Это значение в 2.5 больше указанного в [14]. В нашей модели лучшее соответствие эксперименту дает использование значений коэффициента сдвига s, приблизительно в 1.5 раза больших приведенных в [14]. Таким образом, коэффициенты сдвига и уширения, при соответствующем методическом подходе, могут быть экспериментально определены из спектров СЛ. Значение S0 для наших экспериментальных результатов определяется инструментальной полушириной щели и составляет 0.13 нм.

Мы вычисляли форму линии для произвольной плотности возмущающей среды, используя в качестве начального спектра профиль D-линии Na в пламени. Согласно [14], в пределе растущей плотности профиль линии стремится к гауссовому, независимо от формы межатомного потенциала. Мы аппроксимировали профиль линии G(λ) двумя гауссовыми кривыми, так как компоненты дублета в спектре пламени разрешены:
G(λ,n)=(C1/S1)·exp(-½(Λ1-λ)2/S12)+(C2/S2)·exp(-½(Λ2-λ)2/S22), (2)
где C1, C2 - яркость компоненты; S1, S2 - HWHM; Λ1, Λ2 - длина волны для каждого компонента дублета; λ - текущее значение длины волны. Значения S и Λ зависят от плотности n, согласно формулам (1).
Подставив Sj(n) и Λj(n), где j=1,2 - компоненты дублета, в формулу (2) и задав плотность n от 0 до 100 Амг с шагом 10 Амг, мы получаем форму линии Na для каждого из этих значений плотности (семейство линий 3 на рисунке 2). Мы предположили здесь, что число излучающих атомов постоянно, и сила осциллятора измененной D-линии не изменяется, т.е. не изменяется площадь под каждой кривой. Из приведенной иллюстрации видно, что моделирование линии Na спектром одной плотности дает семейство профилей, которые, следуя увеличению плотности, сдвигаются в длинноволновую область. При этом дублет Na становится полностью неразрешённым уже при n=10 Амг (рис. 2).
Наша идея состояла в том, чтобы учесть изменение плотности возмущающей среды в пузырьке в течение времени высвечивания. Допуская, что ход плотности неизвестен, мы сделали его параметром модели и задали в виде
n(i)=n1+(n2-n1)·iz, (3)
где 0≤i≤1 - переменная (интегрирования), z - параметр кривизны хода плотности. Таким образом, n1, n2 и z являются параметрами модели. Переменная i может иметь физический смысл времени, либо координаты некоторой функции распределения, например, по размерам пузырьков или по локализации их в кавитационном облаке.
Суммарный спектр вычисляется по формуле
H(λ)=k· , (4)
где k - коэффициент нормировки, спектры нормируются на длине волны Λ0 (589 нм для Na).
Моделирование широкой компоненты спектра показало, что использование значений n1>10 Амг даёт лучшее заполнение экспериментального спектра. Однако при этом теряется узкая компонента, которая становится неразрешенной. Ее присутствие в экспериментальных спектрах можно объяснить только вкладом спектров «низкой плотности». Для учета узкой компоненты мы вводим параметр d - добавочную долю спектра «низкой плотности». Как будет показано, d~3 %. Выражение для вычисления спектра:
H(λ)=k·(d·G(λ,0)+(1-d)· (5)
Результаты моделирования нашего спектра СЛ Na и спектра, взятого из [15], представлены на рисунке 2. Учет, в общем случае, уровня континуума спектра с в области линии металла дает окончательное выражение:
H(λ)=с + (1-с)·k·(d·G(λ,0)+(1-d)· (6)
Модель дает очень хорошее воспроизведение формы линий металлов при СЛ. Рассмотрим ее свойства на примере линии Na. Ясно, что излучение при низкой плотности вносит вклад в полосу вблизи несмещенных пиков (узкая компонента спектра), тогда как излучение при высокой плотности увеличивает интенсивность спектра вдали и справа от него (широкая компонента спектра). Рассмотрим поведение модели при варьировании ее параметров. Использование добавочного множителя s~1.5 к s хорошо воспроизводит крутой коротковолновый подъем и более плавный длинноволновый спад интенсивности широкой компоненты. При увеличении s/g изменяется наклон модельного спектра в точке 589 нм, а также уровень спектра слева и справа вдали от максимума. При увеличении значения n2 поднимаются дальние крылья линии, и n2 можно подобрать по отношению интенсивностей вдали и вблизи 589 нм. Уменьшение z при постоянном значении n2 дает расширение профиля линии. Увеличение n1 приводит к заметному росту интенсивности линии справа от 589 нм и смещению максимума. Для компенсации этого можно одновременно уменьшать n2, что приводит к изменению наклона модельного спектра справа от максимума, и его форма становится более симметричной. Уменьшение n1 (n1<10 Амг) дает тот же эффект, что и увеличение d, т.е. увеличение вклада узкой компоненты спектра - спектра "низкой плотности". Для объяснения несмещенных пиков Na, как уже отмечалось, достаточно ~3 % вклада спектра «низкой плотности» в сумму, при этом, вследствие нормировки, существенно изменяется форма всей модельной линии. Это означает, что, если имеет место свечение Na при низкой плотности, оно занимает около 3% интенсивности или времени процесса.
Мы рассмотрели также вариант модели, когда ход плотности задается кривой n(t) (рис. 1), и в котором отсутствует параметр z. Рассмотренный вариант модели на рисунках не показан, но его использование дало следующие результаты. Для лучшей симуляции профиля линии Na также требуется увеличить s в 1.5-2 раза относительно данного [14], однако форма линии воспроизводится хуже, чем при выборе кривой n(i) (3). Возможное объяснение состоит в том, что функция n(i) лучше подходит для учёта динамики плотности в той фазе коллапса, когда светится Na, тогда как n(t) охватывает весь коллапс. Мы рассматривали также аппроксимацию спектральной линии лоренцевой и треугольной формой. Результат моделирования давал такое же хорошее наполнение экспериментальной линии, как в случае гауссовой аппроксимации (2). Мы добавляли в модель зависимость интенсивности излучения от i, что приводило к плохой сходимости расчета. Простое "включение" (при n1) и "выключение" (при n2), согласно (3), дает удовлетворительную сходимость. Функцию n(i) можно также восстановить из наблюдаемого спектра.
В среде MS EXCEL нами реализован интерактивный алгоритм подбора параметров модели. Для автоматического подбора параметров модели по экспериментальному спектру была создана программа на языке "фортран", использующая метод покоординатного спуска. Автоматический подбор параметров возможен с помощью опции MS EXCEL "поиск решения". Задача сводится к минимизации среднеквадратичного отклонения модельного спектра от экспериментального.
Как любая задача оптимизации, данная задача может иметь несколько решений. При моделировании мы нашли три типа решений: (1) 0<n1<n2, d>0; (2) 0~n1<n2, d~0; (3) n1>n2. Наиболее приемлемым является первый тип решения. В случае (3) n1 может принимать очень большие значения (>1000 Амг), что не имеет физического смысла. Второй вариант отвергнут нами, поскольку в этом случае не удается представить в виде числового значения d.
Предложенная модель пригодна для численного разделения узкой и широкой компонент линии металла, как это отмечено в [3, 20], а также численного разделения этих компонент от излучения континуума.
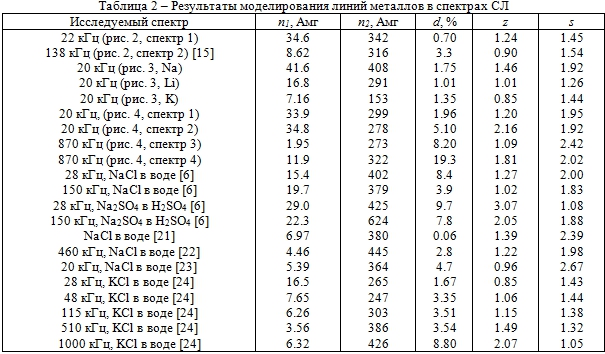
В таблице 2 приведены результаты расчетов для спектров рисунков 2-4 и ряда спектров СЛ, взятых из различных источников. При расчетах из спектров вычитался уровень континуума c. Этот параметр в таблицах не приводится, так как эмиссия континуума не связана с эмиссией Na. Главный результат заключается в том, что свечение щелочных металлов начинается при плотностях порядка 10-20 Амг, прекращается при 200-400 Амг. Доля d узкой компоненты линии в спектре СЛ составляет 1-10 %. Этот параметр наиболее чувствителен к условиям эксперимента, таким как частота ультразвука, время облучения, небольшие добавки газовых примесей [20]. Кривизна хода плотности z имеет значения порядка 1-2. Этот результат еще раз указывает, что свечение широкой компоненты происходит на нарастающей части кривой плотности, то есть вдали от момента tp на врезке рис. 1. Дополнительный множитель s к коэффициенту сдвига s имеет значения порядка 1.5. Это может означать, что для высоких плотностей значения s и g могут отличаться от табличных значений.
На рисунке 3 представлены спектры СЛ 3 М водных растворов KCl, NaCl и LiCl, измеренные на частоте 20 кГц, вместе с расчетными спектрами с использованием модели. Для сравнения показаны спектры солей в пламени.
В спектре K явно выражена дублетная структура. Сдвиг максимумов относительно пиков в пламени составляет ~0.3 нм в красную область. FWHM каждой линии, учитывая кривизну и наклон спектра, составляет около 2.5 нм. Уширение и сдвиг линии аналогичны наблюдаемым для K в [24] для частот ультразвука 28 и 48 кГц.
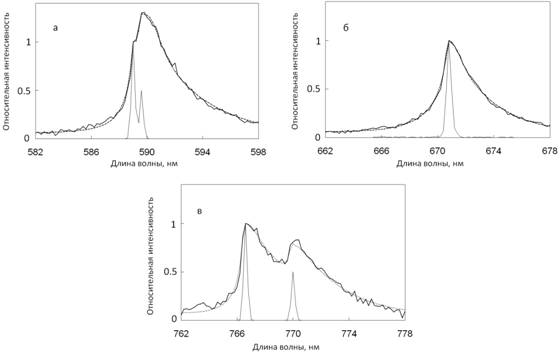
Рис. 3 – Линии металлов в экспериментальных спектрах СЛ водных растворов (а) NaCl, (б) LiCl, (в) KCl (сплошные линии) и их модели (пунктирные линии). Параметры моделей приведены в таблице 2. Для сравнения показаны схематические спектры солей в пламени. Спектры нормированы на длине волны первого компонента дублета
В спектре Na наблюдается один пик. Его смещение в красную область относительно первой линии дублета в пламени (589.0 нм) ~0.8 нм. Наблюдается слабый горб, соответствующий первому пику в пламени, но из-за его слабости сдвиг его точно указать нельзя. Учитывая, что естественное расстояние между линиями дублета равно 0.6 нм, можно заключить, что в данном случае вторая (вдвое слабая) компонента дублета (589.6 нм) накладывается на красный склон широкой полосы первой компоненты, давая пик интенсивности на 589.8 нм, смещенный на 0.2 нм. Вследствие этого относительная интенсивность максимума значительно выше единицы (1.3) тогда как для Li и K около 1.1. FWHM линии составляет ~3.6 нм. Если учесть расщепление дублета (0.6 нм), то получим 3 нм - FWHM одиночной линии при СЛ. При разных экспериментальных условиях СЛ натрия для узкой компоненты интенсивность второй линии дублета бывает как ниже, так и выше интенсивности первой линии. В спектре лития наблюдается один пик, смещенный на 0.2 нм в красную сторону. FWHM линии составляет ~2.8 нм. Вследствие того, что компоненты дублета Li расщеплены незначительно (~0.01 нм), в спектрах пламени и СЛ, при нашем разрешении, наблюдается одна линия. Мы не нашли других опубликованных спектров СЛ высокого разрешения для Li. Сравнивая спектры СЛ щелочных металлов, можно видеть сходство структуры широкой компоненты линий при СЛ - сдвиг максимума в красную область составляет 0.2-0.3 нм, FWHM равно 2.5-3 нм. В таблице 3 приведены оценки нижней и верней границы диапазона плотности, в пределах которого происходит высвечивание широкой компоненты линий, сделанные для спектров рисунка 3, вместе с энергией возбуждения соответствующего состояния атома металла.

Примечательно, что с уменьшением энергии возбуждения металла диапазон его свечения двигается в сторону более низких значений плотности. Калий, имеющий наименьшую энергию возбуждения в представленном ряду, начинает светиться при более низкой плотности, т.е. на более ранних стадиях сжатия, чем литий и натрий. В процессе сжатия пузырька последовательно достигаются все более высокие температура и плотность. Возможно, что возбуждение и высвечивание щелочных металлов происходит в порядке возрастания их энергии возбуждения.
В таблице 2 приведены результаты моделирования линии K в спектре СЛ водного раствора KCl, измеренного для различных частот ультразвука, взятые из [24]. Моделирование показывает, что при повышении частоты ультразвука n2 сдвигается в сторону более высоких значений, при этом в спектре существенно вырастает доля узкой компоненты. На частоте 1 МГц в экспериментальном и модельном спектрах K наблюдается ярко выраженный несмещенный дублет и слабо выраженная широкая компонента.
Выделение узкой компоненты линии в спектрах СЛ с увеличением частоты наблюдалась нами и для линии Na, причем эта тенденция усиливалась в растворах с поверхностно-активными свойствами (рис. 4) [5].
Мы исследовали водные растворы NaCl и додецилсульфата Na (SDS) при частотах 20 и 870 кГц. Параметры моделей для спектров приведены в таблице 2. Можно сделать вывод, что более мелкие пузырьки (на частоте 870 кГц) с более стабильной поверхностью излучают более узкую линию. Одним из объяснений может быть ослабление широкой компоненты из-за отсутствия условий для попадания металлов в высокоплотную область внутри пузырька по механизму "microdrop injection" [1]. Возможны также иные механизмы возбуждения, например, электрический разряд [21].
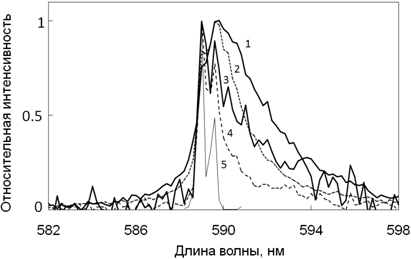
Рис.4 – Линии Na в спектрах СЛ водных растворов NaCl и SDS. (1) - NaCl, 20 кГц; (2) - SDS, 20 кГц; (3) - NaCl, 870 кГц; (4) - SDS, 870 кГц; (5) - спектр пламени с добавлением NaCl. Параметры моделей приведены в таблице 2. Спектры нормированы по максимуму интенсивности
| Финансирование Статья подготовлена по результатам работы, выполненной в рамках госбюджетной НИР ТОИ ДВО РАН, регистрационный номер: АААА-А17-117030110031-6. | Funding The paper presents the results of work carried out within the framework of the state budgetary research and development work of the TOI FEB RAS, registration number: AAAA-A17-117030110031-6. |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Flannigan D. J. Emission from electronically excited metal atoms during single-bubble sonoluminescence / D. J. Flannigan, K. S. Suslick // Phys. Rev. Lett. – 2007. - V. 99. - P. 134301(4).
- Didenko Y. T. Multibubble sonoluminescence spectra of water which resemble single bubble sonoluminescence / Y. T. Didenko, T. V. Gordeychuk // Phys. Rev. Lett. – 2000. - V. 84. - N. 24. - P. 5640-5643.
- Nakajima R. Mechanism of two types of Na emission observed in sonoluminescence / R. Nakajima, Y. Hayashi, P. Choi // Japanese J. Appl. Phys. – 2015. - V. 54. – P. 07HE02
- Казачек М. В. Одна простая модель формы D-линии Na в спектрах сонолюминесценции М. В. Казачек, Т. В. Гордейчук // Письма в ЖТФ. – 2011. - Т. 37. - № 6. - С. 39-48.
- Гордейчук Т. В. Влияние частоты ультразвука на форму D-линии Na в спектрах сонолюминесценции водных растворов хлорида и додецилсульфата натрия / Т. В. Гордейчук, М. В. Казачек // Письма в ЖТФ. – 2014. - Т. 40. - № 23. - С. 31-40.
- Hatanaka S. Sonoluminescence of alkali-metal atoms in sulfuric acid: comparison with that in water / S. Hatanaka, S. Hayashi, P. K. Choi // Jap. J. Appl. Phys. – 2010. - V. 49. – P. 07HE
- Казачек М. В. Оценка пикового давления кавитации по структуре D-линии Na в спектрах сонолюминесценции / М. В. Казачек, Т. В. Гордейчук // Письма в ЖТФ. – 2009. - Т. 35. - № 4. - С. 87-94.
- Brenner M. P. Single-bubble sonoluminescence / M. P. Brenner, S. Hilgenfeldt, D. Lohse // Rev. Mod. Phys. – 2002. - V. 74. - P. 425-484.
- Chu H. C. Precursor luminescence near the collapse of laser-induced bubbles in alkali-salt solutions / H. C. Chu, S. Vo, G. A. Williams // Phys. Rev. Lett. – 2009. - V. 102. - P. 204301.
- An Yu. Diagnosing temperature change inside sonoluminescing bubbles by calculating line spectra / Yu. An, Ch. Li // Phys. Rev. E. – 2009. - V. 80. - P. 046320
- Gompf B. Resolving sonoluminescence pulse width with time-correlated single photon counting / B. Gompf, R. Gunther, G. Nick and others // Phys. Rev. Lett. – 1997. - V. 79. - P. 1405-1408.
- Giri A. Measured pulse width of sonoluminescence flashes in the form of resonance radiation / A. Giri, V. H. Arakeri // Phys. Rev. E. – 1998. - V. 58. - N. 3. – P. R2713.
- Matula T. J. Optical pulse width measurements of sonoluminescence in cavitation-bubble fields / T. J. Matula, R. A. Roy, P. D. Mourad // J. Acoust. Soc. Am. – 1997. - V. 101. - N. 4. - P. 1994-2002.
- Allard N. The effect of neutral nonresonant collisions on atomic spectral lines / N. Allard, J. Kielkopf // Rev. Mod. Phys. – 1982. - V. 54. - P. 1103-1182.
- Choi P. K. Hayashi Y. Sonoluminescence of Na atom from NaCl solutions doped with ethanol / P. K. Choi, S. Abe, // J. Phys. Chem. B. – 2008. - V. 112. - P. 918-922.
- Гордейчук Т. В. Экспериментальное наблюдение интенсивного роста сонолюминесценции металлов под влиянием давления и температуры / Т. В. Гордейчук, М. В. Казачек // Оптика и cпектроскопия. – 2009 - Т. 106. № 2. – С. 274-277
- Flint E. B. Sonoluminescence from alkali-metal salt solutions / E. B. Flint, K. S. Suslick // J. Phys. Chem. – 1991. - V. 95. - P. 1484-1488.
- Storey B. D. Water vapour, sonoluminescence and sonochemistry / B. D. Storey, A. J. Szeri // Proc. R. Soc. London. Ser. A. – 2000. - V. 456. - P. 1685-1709.
- Didenko Y. T. Effect of noble gases on sonoluminescence temperatures during multibubble cavitation / Y. T. Didenko, III W. B. McNamara, K. S. Suslick // Phys. Rev. Lett. – 2000. - V. 84. - N. 4. - P. 777-780.
- Hayashi Y. Two components of Na emission in sonoluminescence spectrum from surfactant aqueous solutions / Y. Hayashi, P. Choi // Ultrason. Sonochem. – 2015. - V. 23. - P. 333-338.
- Маргулис М. А. Сонолюминесценция / М. А. Маргулис // УФН. – 2000. - Т. 170. - № 3. - С. 263-287.
- Sehgal C. Sonoluminescence of argon saturated alkali metal salt solutions as a probe of acoustic cavitation . C. Sehgal, R. P. Steer, R. G. Sutherland, R. E. Verrall // J. Chem. Phys. – 1979 - V. 70 - P. 2242-2248.
- Zhan C. An experiment on multibubble sonoluminescence spectra in sodium chloride solution / C. Zhan, X. JunFeng, H. Wei and others // Chin. Sci. Bull. - 2008. - V. 53. - N. 10. - P. 1468-1472.
