НОВЫЙ ПОДХОД К УСКОРЕНИЮ МЕТОДА D-MORPH ДЛЯ ПОИСКА ОПТИМАЛЬНОГО КВАНТОВОГО УПРАВЛЕНИЯ

Жданов К.Е.

ORCID: 0000-0003-2290-6324, Аспирант, Санкт-Петербургский государственный университет

НОВЫЙ ПОДХОД К УСКОРЕНИЮ МЕТОДА D-MORPH ДЛЯ ПОИСКА ОПТИМАЛЬНОГО КВАНТОВОГО УПРАВЛЕНИЯ

Аннотация

В работе вводятся новые поправки различных порядков малости к методу D-MORPH для поиска оптимального управления квантовой системой в задаче реализации желаемой унитарной эволюции за счет использования полной формы выражения производной от операторной экспоненты, заданной на алгебре Ли. Включение в метод таких поправок, учитывающих информацию о коммутаторах гамильтониана системы, приводит к более быстрому нахождению оптимального управления, даже по сравнению с улучшенной версией метода, опубликованной автором ранее.

Ключевые слова: квантовые системы, оптимальное управление, оператор эволюции, алгебры Ли, квантовые вычисления.

 

Zhdanov K.E.

ORCID: 0000-0003-2290-6324, Postgraduate Student, St. Petersburg State University

NEW APPROACH TO ACCELERATING THE METHOD OF D-MORPH FOR THE SEARCH OF OPTIMUM QUANTUM CONTROL

Abstract

The article introduces new corrections of various orders of smallness to the D-MORPH method for finding the optimal control of a quantum system in the problem of realizing the desired unitary evolution by using the complete expression of the derivative of the operator exponent defined on the Lie algebra. Inclusion of the corrections with regard to information on the commutators of the Hamiltonian system into the method leads to faster identification of optimal control, even in comparison with the improved version of the method published by the author earlier.

Keywords: quantum systems, optimal control, evolution operator, Lie algebras, quantum computations.

Введение

Одним из часто используемых методов для построения оптимального управления квантовыми системами является метод D-MORPH [3]-[5][7][8], который обеспечивает минимизацию заданного критерия качества.

Алгоритм D-MORPH основан на численном решении специально построенной системы обыкновенных дифференциальных уравнений с помощью метода Рунге–Кутты четвертого порядка с переменным шагом по фиктивному параметру s, который обозначает прогресс минимизации функционала качества, что часто требует довольно продолжительного численного интегрирования. Как было показано в опубликованной ранее автором работе [1], метод D-MORPH можно ускорить за счет использования информации о различных коммутаторах гамильтониана квантовой системы.

В данной работе приводится новый способ получения поправок различного порядка малости к методу D-MORPH для ускорения поиска оптимальных управлений за счет использования полной формы производной от операторной экспоненты, заданной на алгебре Ли. Полученные поправки напоминают по форме поправки, найденные автором ранее в [1], поэтому производится их сравнение на примере численной реализации одного квантового гейта, и показывается, что новый метод работает быстрее.

Ранее полученный метод 

Для реализации в N-мерной квантовой системе с M управлениями  к моменту времени T желаемого оператора эволюции  метод  D-MORPH предлагает решить систему дифференциальных уравнений

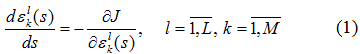
на большом отрезке , где  — функционал качества управлений,  — постоянные значения управлений на отрезке  — параметр, показывающий прогресс метода D­­-MORPH,  – операция взятия следа матрицы, — эрмитово-сопряженный оператор к   — оператор эволюции системы на отрезке .

В работе [1] были предложены поправки различных порядков к методу D-MORPH, которые получаются за счет интегрирования системы по t:

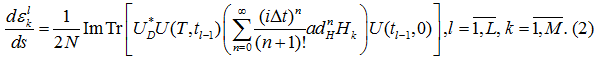
где,  — гамильтониан системы на отрезке ,   — коммутатор матриц  и . Оригинальный метод D-MORPH получается при формальном приравнивании , после чего остается лишь первый член ряда (2). Как было показано в [1], улучшенный метод (2) приводит к минимуму функционала качества быстрее и требует интегрирования системы дифференциальных уравнений на меньшем отрезке , чем оригинальный метод D-MORPH.

Новый способ получения улучшенного метода

Имеется еще один способ получения аналогичных поправок, основанный на более аккуратном и теоретически верном вычислении производной функционала качества . Аналогично работе [2], здесь используется полная форма производной по параметру  от операторной экспоненты , которая является оператором эволюции системы с гамильтонианом H на интервале . Данная форма известна из теории групп и алгебр Ли [9, С. 15] и, в случае квантовой системы, записывается в виде

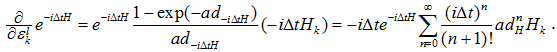
В предыдущей работе [1] использовался только один член с , что является аналогом классической производной от экспоненциальной функции. Из приведенной выше формулы видно, что ошибка такого приближения равна , что может сказаться на точности вычислений при использовании больших шагов по времени, поэтому в данной работе используется полное выражение производной, что должно положительно сказаться на точности нового метода. После подстановки данного выражения в систему получается новая система дифференциальных уравнений

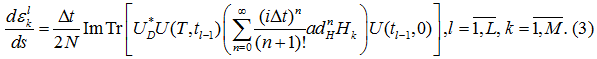
Данная система выглядит аналогично системе полученной ранее в [1] за исключением наличия в системе множителя , и того факта, что она более точно описывает производную операторной экспоненты. Ожидается, что метод будет давать более точные результаты, чем метод , который в свою очередь дает более точные и быстрые результаты, чем D-MORPH. К тому же аналогично методу в сравнении с D-MORPH, ожидается, что метод будет давать верное решение быстрее, чем .

Численный эксперимент

Для экспериментального подтверждения большей точности и скорости метода по сравнению с методом были использованы лишь первые два члена данных методов (с ) для решения задачи из области квантовых вычислений — реализации квантового гейта контролируемого отрицания CNOT [6, С. 21] в квантовой системе, состоящей из двух частиц со спином , описываемой безразмерным гамильтонианом

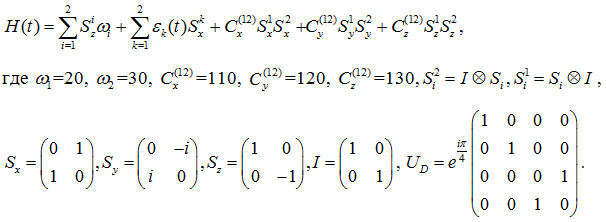
Таким образом, было проведено сравнение двух моделей (были взяты только члены рядов с индексами ), записанных в следующем виде.

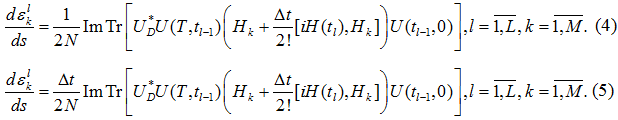
Решение данных систем производилось с помощью метода MATLAB ode45 [10] с нулевыми начальными управлениями на четырехъядерном процессоре Intel Core i7 2.20 ГГц с 12 Гб ОЗУ. Параметры задачи принимали следующие значения: T=5, 10; L=150, 300; S=5000. Вычисления останавливались, когда достигалось значение , т. е. ошибка в реализации гейта меньше 10^-7. Результаты сравнения приведены в таблице.

Таблица 1

	T=10, L=300		T=10, L=150		T=5, L=300		T=5, L=150
Метод	(4)	(5)	(4)	(5)	(4)	(5)	(4)	(5)
Конечное S	70	2089	73	1097	81.1	4866.5	117.8	3532.2
Время, с.	348	317	174.8	158.8	240.8	225.7	99	94.3
Макс. шаг	0.19	5.6	0.14	2.1	0.3	19.4	0.4	13

Из таблицы видно, что предложенный в данной работе новый метод всегда достигает заданной точности за меньшее время, но на большем отрезке интегрирования [0, S], чем метод . К тому же метод допускает использование больших шагов интегрирования, что часто является предпочтительным. Стоит отметить, что аналогичное исследование также было проведено для вариантов методов и с одним лишь членом n = 0 (не показано в таблице), и новый метод оказывался почти всегда хуже оригинального метода D-MORPH — требовал большего времени на вычисления, большего отрезка интегрирования и часто даже не сходился к приемлемому приближению к оптимальному решению.

Выводы

В работе был представлен новый способ получения поправок различного порядка малости к методу построения оптимального квантового управления D-MORPH. Полученные поправки оказались аналогичны найденным автором ранее в работе [1], за исключением наличия у нового метода сомножителя пропорционального шагу по времени, использованном для дискретизации управлений и тому факту, что новый метод более точно описывает производную функционала качества. На примере решения задачи максимально точной реализации квантовой логической операции CNOT в системе, состоящей из двух квантовых частиц, было продемонстрировано, что новый способ получения поправок к методу D-MORPH действительно дает ускорение вычислений по сравнению с ранее полученным методом, который в свою очередь дает ускорение по сравнению с методом D-MORPH. Даже включение одного дополнительного члена в метод позволяет реализовать квантовую операцию быстрее. Примечательно, однако, что при сравнении оригинального метода и нового метода без использования поправок (случай n = 0), новый метод почти всегда оказывался медленнее, а иногда и вовсе не сходился – информация о коммутаторах гамильтониана системы является существенной для нового метода. При отсутствии подобной информации лучшее, что можно сделать — это использовать оригинальный метод D-MORPH. Таким образом, использование теоретически точной формы производной при выводе поправок позволяет еще больше улучшить точность и производительность метода построения оптимального квантового управления, что делает его пригодным для использования на вычислительных системах с небольшими мощностями.

Список литературы на английском языке / References

1. Жданов К. Е. Улучшение метода D-MORPH для поиска оптимального квантового управления / К.Е. Жданов // Международный научно-исследовательский журнал. 2016. № 6 (48) Часть 5. С. 94–99.
2. de Fouquieresa P. Second order gradient ascent pulse engineering / P. de Fouquieresa, S. G. Schirmera, S. J. Glaserb, et. al. // Journal of Magnetic Resonance. 2011. Vol. 212(2). P. 412–417.
3. Moore K. W. Search complexity and resource scaling for the quantum optimal control of unitary transformations /  K. W. Moore, R. Chakrabarti, G. Riviello, et. al. // Phys. Rev. A.2011. Vol. 83(1).
4. Moore K. W. Exploring constrained quantum control landscapes / K. W. Moore, H. Rabitz // The Journal of Chemical Physics. 2012. Vol. 137(13).
5. Moore Tibbetts K. Exploring the trade-off between fidelity and time optimal control of quantum unitary transformations / K. Moore Tibbetts, C. Brif, M. D. Grace, et. al. // Phys. Rev. A. 2012. Vol. 86(6).
6. Nielsen M. A. Quantum Computation and Quantum Information: 10th Anniversary Edition / M. A. Nielsen, I. L. Chuang. New York: Cambridge University Press, 2010. 702 p.
7. Riviello G. Searching for quantum optimal controls in the presence of singular critical points / G. Riviello, C. Brif, R. Long, et. al. // Phys. Rev. A. 2014.Vol. 90(1).
8. Riviello G. Searching for quantum optimal controls under sever constraints / G. Riviello, K. Moore Tibbetts, C. Brif, et. al. // Phys. Rev. A. 2015. Vol. 91(4).
9. Rossmann W. Lie Groups: An Introduction Through Linear Groups / W. Rossmann. New York: Oxford University Press, 2006. 265 p.
10. Shampine L. F. The MATLAB ODE Suite / L. F. Shampine, M. W. Reichelt // SIAM Journal on Scientific Computing. 1997. Vol. 18(1). P 1–22.

Список литературы на английском языке / References in English

1. Zhdanov К. Е. Uluchshenie metoda D-MORPH dlya poiska optimal'nogo kvantovogo upravleniya [an improvement of D-MORPH method for finding quantum optimal control] / K. Е. Zhdanov // Mezdunarodnyj naucno-issledovatel’skij zurnal [International research journal]. 2016. № 6 (48) Part 5. P. 94–99. [in Russian]
2. de Fouquieresa P. Second order gradient ascent pulse engineering / P. de Fouquieresa, S. G. Schirmera, S. J. Glaserb, et. al. // Journal of Magnetic Resonance. 2011. Vol. 212(2). P. 412–417.
3. Moore K. W. Search complexity and resource scaling for the quantum optimal control of unitary transformations /  K. W. Moore, R. Chakrabarti, G. Riviello, et. al. // Phys. Rev. A.2011. Vol. 83(1).
4. Moore K. W. Exploring constrained quantum control landscapes / K. W. Moore, H. Rabitz // The Journal of Chemical Physics. 2012. Vol. 137(13).
5. Moore Tibbetts K. Exploring the trade-off between fidelity and time optimal control of quantum unitary transformations / K. Moore Tibbetts, C. Brif, M. D. Grace, et. al. // Phys. Rev. A. 2012. Vol. 86(6).
6. Nielsen M. A. Quantum Computation and Quantum Information: 10th Anniversary Edition / M. A. Nielsen, I. L. Chuang. New York: Cambridge University Press, 2010. 702 p.
7. Riviello G. Searching for quantum optimal controls in the presence of singular critical points / G. Riviello, C. Brif, R. Long, et. al. // Phys. Rev. A. 2014.Vol. 90(1).
8. Riviello G. Searching for quantum optimal controls under sever constraints / G. Riviello, K. Moore Tibbetts, C. Brif, et. al. // Phys. Rev. A. 2015. Vol. 91(4).
9. Rossmann W. Lie Groups: An Introduction Through Linear Groups / W. Rossmann. New York: Oxford University Press, 2006. 265 p.
10. Shampine L. F. The MATLAB ODE Suite / L. F. Shampine, M. W. Reichelt // SIAM Journal on Scientific Computing. 1997. Vol. 18(1). P 1–22.