МОДЕЛИРОВАНИЕ ОРИЕНТАЦИОННЫХ ЭФФЕКТОВ В КРИСТАЛЛЕ КРЕМНИЯ ПРИ ЭНЕРГИЯХ В СОТНИ ГЭВ

Манвелян Д.Х.¹, Уджуху Д.А.²

¹ ORCID: 0000-0001-7021-9129, Магистрант,

² ORCID: 0000-0001-9193-3604, Магистрант,

^1,2 Кабардино-Балкарский государственный университет им. Х.М. Бербекова, Нальчик, Россия

МОДЕЛИРОВАНИЕ ОРИЕНТАЦИОННЫХ ЭФФЕКТОВ В КРИСТАЛЛЕ КРЕМНИЯ ПРИ ЭНЕРГИЯХ В СОТНИ ГЭВ

Аннотация

Приведены расчёты спектров интенсивности гамма излучения электронов с энергиями, превышающими сотни ГэВ, в ориентированном кристалле кремния. Анализ основан на компьютерном моделировании с учётом когерентного и некогерентного вкладов в излучение, а также многократного рассеяния и демпинга поперечной энергии. Учитывались квантовые эффекты, возникающие при излучении жёстких фотонов. Показано наличие эффекта сильного поля, а также отсутствие аддитивности вкладов когерентной и некогерентной частей в интенсивность излучения. Установлено, что в крайне жёсткой части спектра вклад некогерентного излучения может быть преобладающим, также как и в мягкой части, однако в основной части спектра когерентное излучение может превышать некогерентную часть на два порядка.

Ключевые слова: ориентированный кристалл, каналирование, сильные поля, излучение гамма квантов, ультрарелятивистские электроны.

Manvelyan D.H.¹, Udzhuhu D.A.²

¹ ORCID: 0000-0001-7021-9129, Master's degree student,

² ORCID: 0000-0001-9193-3604, Master's degree student,

^1,2 Kabardino-Balkarian State University named after H. M. Berbekov, Nalchik, Russia

SIMULATION OF ORIENTATION EFFECTS IN SILICON CRYSTAL UNDER ENERGIES IN HUNDREDS OF GIGAELECTRONVOLTS

Abstract

The gamma-ray intensity spectra of electrons with energies exceeding hundreds of gigaelectronvolts is calculated in an oriented silicon crystal. The analysis is based on computer simulation, taking into account coherent and incoherent contributions to radiation, as well as multiple scattering and dumping of transverse energy. Quantum effects arising from the emission of hard photons were taken into account. The presence of a strong field effect is shown, as well as the lack of additivity of the contributions of the coherent and incoherent parts to the radiation intensity. It is found that in the extremely hard part of the spectrum the contribution of incoherent radiation can be predominant, as well as in the soft part, however, in the main part of the spectrum, coherent radiation can exceed the incoherent part by two orders of magnitude.

Keywords: oriented crystal, channeling, strong fields, gamma-ray emission, ultrarelativistic electrons.

Введение

Ориентированные кристаллы позволяют изучать эффекты сильного поля в лабораторных условиях. Под сильным электромагнитным полем понимается такое электрическое (или магнитное) поле, напряжённость которого  в собственной системе отсчёта электрона, на который действует это поле, превышает критическое поле Швингера . В этом случае инвариант  оказывается порядка или больше единицы, причём [1]

   (1)

где χ - параметр Швингера,  - тензор внешнего электромагнитного поля,  - Лоренц фактор электрона, движущегося в данном поле , V - скорость электрона, e и m - его заряд и масса покоя, C - скорость света в вакууме,  - 4-импульс электрона. Появление Лоренц-фактора γ в выражении (1) связано с тем, что эта формула записана для лабораторной системы координат, в которой изучается взаимодействие, тогда как в собственной системе координат, в которой определяется инвариант χ, поле в γ раз больше в силу преобразований Лоренца. Критическое поле Швингера равно

  (2)

где   - сила, соответствующая критическому полю.

Целью нашей работы является изучение эффекта сильного поля для процессов электромагнитного излучения электронов с энергиями более 100 ГэВ при движении через кристалл кремния вдоль направления <110>. Актуальность данного вопроса усиливается тем обстоятельством, что аналогичные эффекты имеют место также при движении электронов в полях сверхмощных лазеров [2], [3]. Конкретные расчёты спектров излучения электронов, движущихся в поле тераваттных лазеров, приводятся в работе [4].

Потенциал атомной цепочки в ориентированном кристалле

В ориентированных кристаллах, когда электрон движется под малыми углами к кристаллографическим осям, напряжённости поля примерно равна , где Z атомный номер кристалла, d - расстояние между атомами в атомной цепочке вдоль выбранного направления,  - параметр экранирования Томаса-Ферми. В реальных кристаллах эта величина составляет примерно . Это означает, что при энергиях электронов свыше 100 ГэВ, когда , значение параметра Швингера (1) становится порядка единицы. На самом деле, квантовые эффекты в излучении и рождения пар гамма квантами проявляются в ориентированных кристаллах уже при  [5]. Сила, действующая со стороны потенциала атомной цепочки кристалла на электрон на расстоянии r от этой цепочки равна

   (3)

где  - непрерывный потенциал атомной цепочки [1, 5], а градиент в (3) берётся только по поперечным к оси цепочки координатам.

На рисунке 1 показаны результаты нашего расчёта непрерывного потенциала атомной цепочки <110> кристалла кремния (сплошная красная кривая, правая шкала) и соответствующей силы (пунктирная кривая, левая шкала), как функции расстояния до цепочки.

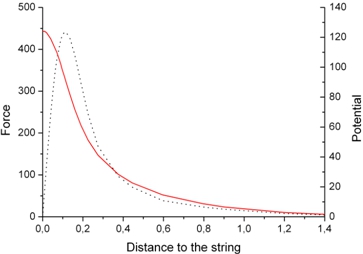
Рис. 1 – Непрерывный потенциал атомной цепочки в кристалле кремния <110> в эВ: сплошная кривая (правая шкала) и соответствующая сила в эВ/Å  (точки, левая шкала) как функции расстояния до атомной цепочки r в Å

Расстояния до цепочки r показаны на Рис. 1 в ангстремах (ось абсцисс). Потенциал рассчитывался нами в приближении Дойля-Тёрнера [6, 7]. Из этого рисунка следует, что глубина потенциальной ямы в данном случае составляет  эВ, а сила достигает максимального значения на расстоянии от цепочки , что примерно равно значению параметра Томаса-Ферми  и составляет в максимуме 450 эВ/Å. Масштаб расстояний выбран на Рис.1 таким образом, что максимальное значение r примерно соответствует поперечному радиус канала, который равен , где N - число атомов кристалла в единице объёма. В рассматриваемом случае .

Сечения излучения фотонов

Дифференциальная вероятность излучения фотона с энергией  электроном с энергией  за единицу времени определяется в приближении постоянного поля квантовой синхротронной формулой [1], [8]:

где аргумент экспоненты     (6) здесь  - Лоренц фактор,     (7)

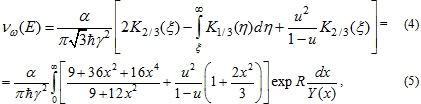
Функция  в (6) представляет собой линию наискорейшего спуска фазы для интегрального представления функций Макдональда . Представление сечения излучения, задаваемое выражением (5), было впервые получено М.Х.Хоконовым (см., например, [8]) и гораздо удобнее, чем стандартная формула (4), содержащая функции Макдональда , так как выражение (5) представляет собой быстросходящийся интеграл, где аргумент ξ (7) входит только в экспоненциальный фактор. Эта формула получена методом мнимого времени. Формулы (4)  (7) переходят в классические формулы для синхротронного излучения при малых значениях параметра поля .

Полная вероятность излучения фотона равна

   (8)

На Рис.2 показана полная вероятность излучения фотона на единице длины (в 1/мкм) в кристалле кремния <110> при энергии электронов E = 150 ГэВ как функция расстояния до атомной цепочки r, заданного в ангстремах.

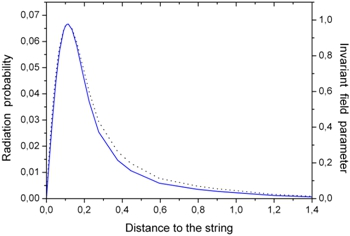
Рис. 2 – Вероятность излучения гамма кванта на единице длины в 1/мкм (сплошная кривая, левая шкала) и инвариантный параметр поля χ (пунктирная кивая, правая шкала) как функции расстояния до атомной цепочки r (в Å) в кристалле кремния <110> при энергии электронов 150 ГэВ

Правая шкала показывает зависимость параметра Швингера (1) от расстояния r для этого же случая (пунктирная кривая). Из Рис.2 следует, что зависимости  ведут себя как функции r почти одинаково, а максимум кривых совпадает с максимумом на Рис.1. Значение параметра Швингера в максимуме достигает значения , то есть излучение носит чисто квантовый характер. При этом излучается  фотонов на микрометр. Усреднённое по всей поперечной плоскости канала значение сечения излучения равно в данном случае примерно 0.012 фотон/мкм, что для кристалла с толщиной 1000 мкм даёт примерно 12 фотонов на один электрон. Таким образом, при рассматриваемых энергиях имеет место множественный характер излучения фотонов отдельным электроном. Заметим, что полное сечение излучения (8), в отличие от дифференциального сечения (4) и (5), слабо зависит от полной энергии электронов E.

Электроны, движущиеся в поле атомной цепочки можно разделить на две группы в зависимости от характера их поперечного движения. Электроны с отрицательными поперечными энергиями  совершают финитное поперечное движение и называются каналированными, тогда как электроны с  имеют инфинитные поперечные траектории и называются квазиканалированными. Доля последних, как правило, значительно превышает долю каналированных электронов и составляет до 70-90 процентов пучка в кристаллах с толщинами 200 – 2000 мкм при углах влёта в канал  - критический угол Линдхарда [1]. Поперечная энергия электрона равна

    (9)

где первый член представляет собой поперечную кинетическую энергию , поперечный импульс по величине равен  - угол между вектором скорости электрона и осью канала (направление которой примем за ось z),  - импульс электрона ,  - релятивистская масса электрона,  - его скорость, m₀ - масса покоя электрона.

При энергиях электронов 150 ГэВ критические углы  равны нескольким десяткам микрорадиан. Не смотря на то, что доля каналированных электронов значительно меньше доли квазиканалированных, существенная часть энергетических потерь и вклад в спектр интенсивности излучения жёстких фотонов во многом обусловлены именно каналированными электронами, так как они проводят больше времени вблизи атомных цепочек, а значит, и сильнее излучают. Для численных оценок полезно знать средние значения потерь энергии на единице длины  <>, среднее число излучаемых фотонов на единице длины <ν> и среднее значение параметра Швингера <χ>. Скобки означают усреднение по все доступной области для электронов с заданной поперечной энергией:

   (10)

причём радиус доступной области  вычисляется из соотношения для поперечной энергии электрона в канале ,  есть поперечная область, доступная электрону с поперечной энергией . Для кремния <110> при E=150 ГэВ наши расчёты дают для квазиканалированных электронов значения: <>=0.0588 ГэВ/мкм, <ν>=0.00741 фотон/мкм и <χ>=0.0897. При этом, для квазиканалированных электронов, в выражении (10) следует положить , где  - радиус канала. В этом случае перечисленные величины не будут зависеть от поперечной энергии, тогда как для каналированных электронов они сильно зависят от . Здесь потери энергии на единице длины связаны с соответствующей вероятностью излучения (4) как

   (11)

Нами проводилось численное моделирование процесса прохождения и излучения электронов с энергией 150 ГэВ через кристалл кремния на основе кода ARR [9]. Аналогичный метод использовался авторами работы [10], которые показали хорошее согласие данного подхода с экспериментальными результатами, полученными в ЦЕРН [5]. Физические принципы, лежащие в основе моделирования, описаны в работах [11], [12].

Численное моделирование и результаты

В расчетах нами учитывалось многократное рассеяние электронов на тепловых колебаниях атомов кристаллической решётки. При этом сечение рассеяния на отдельных атомах вычислялось для атомного потенциала Мольера [7], тогда как непрерывный потенциал атомной цепочки вычислялся на основе потенциала Дойля-Тёрнера. Это связано с тем, что потенциал Мольера лучше описывает область вблизи атома , когда потенциал является существенно кулоновским. С другой стороны, "хвост" потенциала на больших расстояниях лучше описывается потенциалом Дойля-Тёрнера. Предполагалось наличие статистического равновесия в поперечном фазовом пространстве. То есть, пространственное распределение электронов с заданной поперечной энергией  внутри доступной поперечной области  считалось однородным

   (12)

есть вероятность того, что электрон находится на расстояниях в пределах  от цепочки.

Длина свободного пробега электрона между двумя последовательными актами излучения  моделировалось с учётом сложного характера движения электрона в кристалле

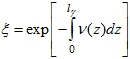   (13)

где ξ есть случайное число, равномерно распределённое на отрезке [0,1]. Между каждыми отдельными актами излучения решалось трансцендентное уравнение (13) для нахождения . Сложный характер движения обусловлен тем, что поперечная энергия электрона меняется стохастическим образом из-за некогерентных актов рассеяния на отдельных атомах кристалла, что приводит к зависимости сечения (т.е. вероятности) излучения от глубины проникновения в кристалл  в выражении (13). Координата точки , в которой происходит излучение фотона, определялась из распределения вероятностей, задаваемого функцией , показанной сплошной кривой на Рис.2, но нормированной на единицу. В расчетах учитывалось уменьшение поперечной энергии в результате излучения, происходящего в точке 

   (14)

где следует брать текущие значения полной и поперечной энергий, которые электрон имел непосредственно перед излучением. Выражение (14) означает, что мы предполагаем, что демпинг поперечной энергии пропорционален кинетической энергии поперечного движения, а также уменьшению полной энергии электронов.

Нами вычислялся спектр интенсивности излучения на заданной толщине кристалла  - есть энергия всех излучённых одним электроном фотонов, лежащая в интервале (), а E₀ - начальная энергия электрона. То есть, здесь  есть полная энергия всех излучённых фотонов

   (15)

где k - число излучённых фотонов. Фактически  есть функция распределения энергетических потерь. Именно эта величина измеряется в экспериментах [5], причём в спектр интенсивности вносит вклад не только излучение в непрерывном потенциале, но и некогерентное тормозное излучение на отдельных атомных ядрах мишени.

Полные потери энергии на излучение в кристалле с толщиной Z будут

   (16)

В отличие от (11) величина (16) определяет потери энергии на конечной длине.

Наряду с когерентным излучением в непрерывном потенциале, задаваемом сечением излучения (4), имеет место также некогерентное тормозное излучение на отдельных атомах кристалла (излучение Бёте-Гайтлера). В аморфном веществе (что эквивалентно разориентированному кристаллу) дифференциальная вероятность некогерентного излучения Бёте-Гайтлера задаётся известным выражением

  (17)

где    (18)

здесь  - радиационная длина, , N - число ядер в 1 см , имеющих заряд Z,  - классический радиус электрона. В случае каналирования, когда , плотность ядер внутри доступной области превышает эту же величину в аморфной среде в  раз. В расчетах нами учитывался этот фактор. В области жёстких частот излучения сечение когерентного излучения (5) экспоненциально падает с увеличением энергии излучаемых фотонов, что приводит к тому, что в области энергий фотонов  сечение Бетё-Гайтлера (17) может значительно превышать сечение (4), тогда как в основной части спектра сечение когерентного излучения (4) доминирует на один-два порядка.

На Рис.3 показан спектр интенсивности излучения для электронов с энергией 150 ГэВ в кристалле кремния <110> с толщиной 1400 мкм. Угловая расходимость электронного пучка на входе в кристалл равна . Интенсивность даётся в единицах интенсивности в аморфной мишени с той же толщиной, то есть в единицах Az, где A определяется из (18) и по оси ординат отложена величина , что показывает увеличение интенсивности излучения в кристалле по сравнению с аморфной мишенью.

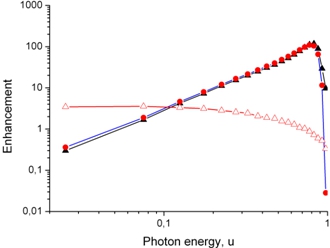
Рис. 3 – Спектр интенсивности излучения для электронов с энергией 150 ГэВ в кристалле кремния <110> с толщиной 1400 мкм. Интенсивность даётся в единицах интенсивности в аморфной мишени с той же толщиной, энергия фотона измеряется в единицах первоначальной энергии электрона. Светлые треугольные и круглые символы – некогерентный и когерентный вклады, соответственно, чёрные треугольники – суммарный спектр

 

Энергия фотона на Рис.3 измеряется в единицах первоначальной энергии электрона, то есть по оси абсцисс отложена величина . Светлые треугольные символы показывают вклад некогерентного излучения (красная кривая), круглые символы когерентный вклад (синяя кривая). Чёрные треугольники, соединённые чёрной линией  – суммарный спектр.

Из Рис.3 следует, что максимум спектра в ориентированном кристалле приходится на энергии излучения , причём интенсивность излучения на два порядка превышает интенсивность в аморфной мишени. Некогерентный вклад доминирует в область мягких (ω<0,1E) и, наоборот, в области жёстких частот, когда .

Выводы

Нами показано, что при энергиях 150 ГэВ спектральная интенсивность излучения электронов, проходящих через кристалл вблизи направления <110>, может более чем на два порядка превосходить аналогичную величину в неупорядоченной среде (что эквивалентно разориентированному кристаллу). В основном излучение исходит из области пространства  вблизи атомной цепочки. Интересной особенностью спектров интенсивности является то, что отсутствует аддитивность вкладов когерентной и некогерентной составляющих, то есть суммарный спектр на Рис.3 не равен сумме спектров, показанных светлыми треугольными и круглыми символами. Это связано с тем, что сумма (15) в случае реального полного спектра содержит в себе, как когерентные, так и некогерентные слагаемые, тогда как кривые, определяющие парциальные вклады на Рис.3 содержат слагаемые только одного типа. В области очень жёстких фотонов с энергиями порядка первоначальной энергии электронов, интенсивность некогерентного излучения может превышать интенсивность когерентной части, тогда как в остальной части спектра значительно преобладает когерентное излучение.

Список литературы / References

1. Байер В. Н. Электромагнитные процессы при высокой энергии в ориентированных монокристаллах / БайерВ.Н., Катков В. М., Страховенко В. М. // Новосибирск. – Наука. – 1989.
2. Di Piazza A. Extremely high-intensity laser interactions with fundamental quantum systems / Di Piazza A., Muller C., Hatsagortsyan K. Z. and others // Review of Modern Physics. – 2012. – No.3. – Vol. 84. – P. 1177-1228.
3. Khokonov M. Kh. The relationship of channeling radiation to Thomson scattering and the relative efficiency of X-ray production by intense electron beams / Khokonov M. Kh., Carrigan R. A. Jr. // Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms B. – 1998. – V. 145. – P. 133 - 141.
4. Батова А.Э. Высшие гармоники в спектрах излучения электронов высоких энергий в поле мощных лазеров / Батова А.Э., Кипшиева Э.А., Мамова А.З. // Научный альманах. – 2016. – № 2-2 (16). – С. 425 - 428.
5. Uggerhoj U. The interaction of relativistic particles with strong crystalline fields / Uggerhoj U. // Reviews of Modern Physics. – 2005. – V. 77. – P. 012703-1-11.
6. Doyle P. A. Relativistic Hartry-Fock X-ray and electron scattering factors / Doyle P. A., Turner P .S. // Acta Crystallographica A. – 1968. – V. 24 – No. 3. – P. 390-397.
7. Дедков Г. В. Межатомные потенциалы взаимодействия в радиационной физике / Дедков Г. В. // Успехи физических наук. – 1995. – Т. 165. – С. 919-953.
8. Khokonov M. Kh. High energy limit of single photon channeling radiation spectrum / Khokonov M. Kh., Efendiyev K. V. // Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. – 2006. – V. 252. – P. 36-43.
9. Хоконов М. Х. Свидетельство о государственной регистрации программ для ЭВМ / Хоконов М. Х., Тлячев В. Б. // 2015. № 2015661450 от 28.10.2015.
10. Карежева М. А. Влияние кристаллической решётки на спектры интенсивности излучения электронов с энергиями свыше 100 ГэВ / Карежева М. А., Ортанов А. А. // Научный альманах. – 2016. – № 2-2(16). – C. 439 - 442.
11. Khokonov M. Kh. Influence of electromagnetic radiation on the angular distributions of electrons in oriented crystals / Khokonov M. Kh. // Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms B. – 1996. – V. 119. – P. 63 - 66.
12. Хоконов М. Х. Угловые распределения релятивистских заряженных частиц в ориентированных кристаллах / Хоконов М. Х. // Журнал экспериментальной и теоретической физики. – 1993. – В. 5. – Т.103 – С. 1723-1741.

Список литературы на английском языке / References in English

1. Bayer V.N. Elektromagnitnyye protsessy pri vysokoy energii v oriyentirovannykh monokristallakh [Electromagnetic Processes at High Energy in Oriented Single Crystals] / Bayer V.N., Katkov V.M., Strakhovenko V.M. / Novosibirsk. – Science. – 1989. [in Russian]
2. Di Piazza A. Extremely high-intensity laser interactions with fundamental quantum systems / Di Piazza A., Muller C., Hatsagortsyan K. Z. and Keitel C. H. // Review of Modern Physics. - 2012. - No.3. - Vol. 84.- P. 1177-1228. [in Russian]
3. Khokonov M. Kh. The relationship of channeling radiation to Thomson scattering and the relative efficiency of X-ray production by intense electron beams / Khokonov M. Kh., Carrigan R. A. Jr. // Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms B. - 1998. - V. 145. - P. 133 - 141.
4. Batova A.E. Vysshiye garmoniki v spektrakh izlucheniya elektronov vysokikh energiy v pole moshchnykh lazerov [Higher Harmonics in Emission Spectra of High-energy Electrons in Fields of High-power Lasers] / Batova A.E., Kipshieva E.A., Mamova A.Z. // Scientific almanac. – 2016. – No. 2-2 (16). – P. 425 – 428. [in Russian]
5. Uggerhoj U. The interaction of relativistic particles with strong crystalline fields / Uggerhoj U. // Reviews of Modern Physics. - 2005. - V. 77. - P. 012703-1-11.
6. Doyle P. A. Relativistic Hartry-Fock X-ray and electron scattering factors / Doyle P. A., Turner P .S. // Acta Crystallographica A. - 1968. - V. 24 / - No. 3. P. 390-397.
7. Dedkov G.V. Mezhatomnyye potentsialy vzaimodeystviya v radiatsionnoy fizike [Interatomic Interaction Potentials in Radiation Physics], Dedkov G.V. // Successes of physical sciences. – 1995. – V. 165. – P. 919-953. [in Russian]
8. Khokonov M. Kh. // Nuclear Instruments and Methods in Physics Research Section / Khokonov M. Kh. Khokonov M.Kh., Efendiyev K. V.: Beam Interactions with Materials and Atoms. - 2006. - V. 252. P. 36-43.
9. Khokonov M. Kh. Svidetel'stvo o gosudarstvennoy registratsii programm dlya EVM [Certificate of State Registration of Computer Programs] / Khokonov M. Kh., Tlachev V.B. // 2015. No. 2015661450 dated 10/28/2015.
10. Karezheva M.A. Vliyaniye kristallicheskoy reshotki na spektry intensivnosti izlucheniya elektronov s energiyami svyshe 100 GeV [Influence of Crystal Lattice on Radiation Intensity Spectra of Electrons with Energies Above 100 GeV] / Karezheva M.A., Ortanov A.A. // Scientific almanac. – 2016. No. 2-2 (16). P. 439-442. [in Russian]
11. Khokonov M. Kh. Influence of electromagnetic radiation on the angular distributions of electrons in oriented crystals / Khokonov M. Kh. // Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms B. - 1996. - V. 119. - P. 63 - 66.
12. Khokonov M. Kh. Uglovyye raspredeleniya relyativistskikh zaryazhennykh chastits v oriyentirovannykh kristallakh [Angular Distributions of Relativistic Charged Particles in Oriented Crystals] / Khokonov M. Kh. // Journal of Experimental and Theoretical Physics. - 1993. – B. 5. – V.103 – P. 1723-1741. [in Russian]