МОДЕЛИРОВАНИЕ ИЗОБРАЖЕНИЙ НЕКОГЕРЕНТНЫХ ОБЪЕКТОВ В ТУРБУЛЕНТНОЙ АТМОСФЕРЕ

МОДЕЛИРОВАНИЕ ИЗОБРАЖЕНИЙ НЕКОГЕРЕНТНЫХ ОБЪЕКТОВ В ТУРБУЛЕНТНОЙ АТМОСФЕРЕ

Научная статья

Колосов В.В.¹, Кузнецов М.Ф.^2, *

¹ Институт оптики атмосферы им. В.Е. Зуева СО РАН, Томск, Россия;

² Хакасский государственный университет им. Н.Ф. Катанова, Абакан, Россия

* Корреспондирующий автор (kuznec-mikhail[at]yandex.ru)

Аннотация

Обсуждается применение прилучевого метода решения уравнения переноса излучения для численного моделирования изображений некогерентных объектов в турбулентной атмосфере. Оценивается точность данного метода при различных условиях распространения излучения и его эффективность.

Ключевые слова: турбулентная атмосфера, моделирование изображений, прилучевой метод, уравнение переноса излучения.

MODELING OF IMAGES OF NON-COHERENT OBJECTS IN TURBU-LENT ATMOSPHERE

Research article

Kolosov V.V.¹, Kuznetsov M.F.^2, *

¹ V.E. Zuev Institute of Atmospheric Optics of Siberian Branch of the Russian Academy, Tomsk, Russia;

² Khakassian State University named after N.F. Katanov, Abakan, Russia

* Corresponding author (kuznec-mikhail[at]yandex.ru)

Abstract

The application of the pre-ray-tracing method for solving the radiation transfer equation for the numerical simulation of images of incoherent objects in a turbulent atmosphere is dis-cussed. The accuracy of this method is estimated under various conditions of radiation propaga-tion as well as its effectiveness.

Keywords: turbulent atmosphere, image modeling, radiation method, radiation transfer equation.

Атмосферная турбулентность существенно влияет на процессы распространения излучения и ухудшает условия регистрации изображений объектов. Развитию эффективных методов и алгоритмов моделирования распространения излучения в атмосфере уделяется значительное влияние. Как правило, для решения задач подобного типа используется либо параболическое волновое уравнение [1], [2], [3], либо уравнение для функции когерентности поля второго порядка [4], [5], [9] или фурье-сопряженное ему уравнение переноса излучения [6], [7], [8]. Высокая размерность данных уравнений, необходимость использования метода статистических испытаний требует значительных вычислительных затрат. В данной работе рассматривается метод, позволяющий уменьшить время решения подобных задач.

Поле в плоскости изображения выражается через поле объекта, упавшее на линзу, следующим образом [1]:

   (1)

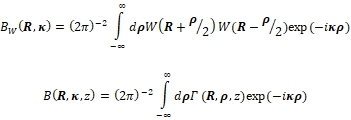Для интенсивности поля в плоскости изображения    (2) в суммарно-разностных координатах в случае произвольной апертурной функции W(r) можно записать следующее выражение [10]    (2) где использовано обозначение  , а подынтегральные функции имеют следующий вид Последняя функция – яркость излучения, представляет собой преобразование Фурье от функции когерентности поля: 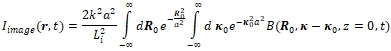Для апертурной функции вида   выражение (2) для интенсивности изображения через яркость излучения примет вид [9]:     (3)

Для яркости излучения в приближении плавного изменения показателя преломления n(R,z,t) может быть записано уравнение [6]

  (4)

решение которого может быть найдено методом характеристик:    (5)

Численное моделирование изображения объектов высокого разрешения на основе выражения (3) в турбулентной атмосфере с использованием метода статистических испытаний [9] сопряжено со значительными вычислительными затратами, поскольку предполагает многократное решение системы уравнений (5). Объем вычислений может быть сокращен, если использовать предлагавшийся ранее авторами подход [13], основывавшийся на развитии метода построения решения в приосевой области пучка [11], [14]. Предполагая, что основной вклад в интенсивность в точке приема будет давать конус лучей, опирающийся на площадку, размеры которой много меньше размеров пучка, представим произвольную характеристику , принадлежащую конусу лучей в виде:

    (6)

где характеристика   удовлетворяет системе уравнений (5) с граничными условиями, заданными в плоскости . Для вариации , используя разложение показателя преломления  около характеристики 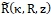 в функциональный ряд Тейлора и ограничиваясь линейными по  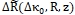слагаемыми, можно получить следующее уравнение:

   (7)

с граничными условиями, заданными в плоскости линзы    (8)

Значение произвольной характеристики  в плоскости объекта может быть определено с помощью (6) через значение единственной характеристики , удовлетворяющей уравнению (5) и якобиан фундаментальной системы решений уравнения (7). Таким образом, данное приближение позволяет построить около характеристики , назовем её опорным лучом, решение для произвольного количества вариаций . Результаты компьютерного эксперимента, обсуждаемые ниже, получены для случаев, когда количество опорных лучей равнялось одному и четырем, а количество вариаций дополняло массив изображения объекта до размеров 8х8, 16х16, 32х32 и 64х64 пикселей.

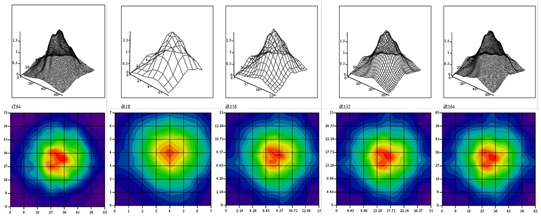
Рис. 1 – Изображение гауссового объекта в турбулентной атмосфере, полученное разными методами при значении радиуса Фрида r_0=0.5: а) эталонное решение методом характеристик для матрицы 64х64; б), в). г). д) решение методом «прилучевого» приближения для матриц 8х8, 16х16, 32х32 и 64х64 соответственно

 

Схема компьютерного эксперимента аналогична [9]. Точность используемого приближения оценивалась путем сравнения решения, полученного в рамках данного приближения, с эталонным решением методом характеристик [9], полученным традиционным путем при решении (5). В качестве тестовой задачи рассматривалось моделирование изображения различных некогерентных объектов, в частности, гауссова пучка с распределением интенсивности  заданного в плоскости объекта на сетке 8х8, в турбулентной среде с кармановским спектром флуктуаций показателя преломления при различных значениях радиуса Фрида . Эталонное решение, полученное с помощью метода характеристик [9], размером 64х64 пикселя (рис. 1, а) и решение в «прилучевом» приближении (рис. 1, б-д) было получено на одних и тех же фазовых экранах (10 экранов) при усреднении по 400 реализациям. В качестве эталонного решения использовалось изображение объекта, полученного с помощью (3-5), размером 64х64 пикселя.

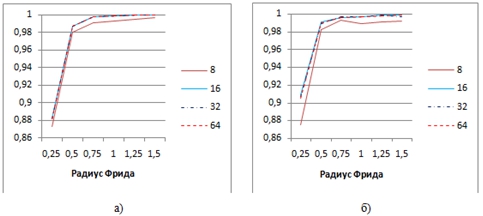
Для расчета коэффициентов корреляции Пирсона эталонного изображения и изображения объекта, полученного в «прилучевом» приближении, последние массивы при необходимости интерполировались с помощью двумерных сплайнов до размера 64х64 пикселя. Анализ результатов на рис. 2 показывает, что при умеренной турбулентности () «прилучевое» приближение дает решение, сравнимое с эталонным, даже для размерностей исходных матриц ≥16. Причем это справедливо и для решений, полученных с одним опорным лучом, и с четырьмя. Решение с четырьмя опорными лучами дает несколько лучший результат, если области с максимальной интенсивностью в плоскости объекта смещены из центра на периферию.

Рис. 2 – Коэффициенты корреляции приближенного решения (а – 1 опорный луч, б – 4 опорных луча) с эталонным при различной степени турбулентности. Цифры у легенды – размерность исходного массива изображения

 

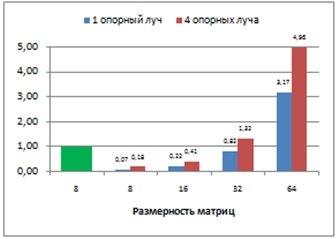
На рис 3 приведены средние времена счета различных методов относительно времени получения эталонного изображения с помощью (4-5) размером 8х8 пикселей. Метод «прилучевого» приближения для матрицы такого же размера в случае одного и четырех опорных лучей требует примерно в десять и в пять раз меньше времени соответственно. Для матриц размером 64х64 пикселя эти времена меньше примерно в двадцать и двенадцать раз соответственно.

Рис. 3 – Относительное время счета различных методов (зеленым цветом обозначено время счета эталонного изображения для матрицы 8х8 пикселей)

 

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Рытов С.М. Введение в статистическую радиофизику. / Рытов С.М., Кравцов Ю.А., Татарский В.И. – М.: Наука, 1978. 463 с.
2. Кандидов В.П. О применении метода статистических испытаний к исследованию распространения волнового пучка в случайно-неоднородной среде / Кандидов В.П., Леденев В.И. //Изв. вузов. Радиофиз. 1981. Т. 24. №4. С. 438-442.
3. Коняев П.А. Модификация метода расщепления для численного ре-шения квазиоптических задач / Коняев П.А. //VI Всес. симпоз. по распространению лазерного излучения в атмосфере. Часть III. Томск, 1981. С. 195-198.
4. Пасманик Г.А. Самовоздействие пучков некогерентного света / Пасманик Г.А. //ЖЭТФ. 1974. Т. 66. №2. С. 490-500.
5. Алешкевич В.А. Самовоздействие неко-герентного светового пучка / Алешкевич В.А., Лебедев С.С., Матвеев А.Н. //Квантовая электроника. 1981. Т. 8. №5. С. 1090-1094.
6. Долин Л.С. О лучевом описании слабо-неоднородных волновых полей / Долин Л.С. //Изв. высш. учебн. заведений. Радиофизика. 1964. Т. 7. №3. С. 559-562.
7. Рытов С.М. Введение в статистическую радиофизику. Часть II. Случайные поля / Рытов С.М. Кравцов Ю.А., Татарский В.И. – М.: Наука, 1978. 463 с.
8. Колосов В.В. О фазовой компенсации рефракци-онных искажений частично когерентных пучков / Колосов В.В., Кузиковский А.В. //Квантовая электроника. 1981. Т. 8. №3. С. 490-494.
9. Дудоров В.В. Коррекция некогерентных изображений объектов в условиях анизопланатизма турбулентности по опорному источнику излучения различной длины волны / Дудоров В.В., Колосов В.В. //Оптика атмосферы и океана. 2010. Т. 23. №5. С. 392-397.
10. Ахманов С.А. Статистическая радиофизика и оптика. Случайные колебания и волны в линейных системах / Ахманов С.А., Дьяков Ю.Е., Чиркин А.С. М.: Физматлит, 2010. 426 с.
11. Воробьев В.В. Уширение светового пучка в нелинейной среде со случайными неоднородностями показателя преломления / Воробьев В.В. // Изв. вузов. Радиофиз. 1970. Т. 13. С. 1053-1060.
12. Vorontsov M.A. Target-in-the-loop beam control: basic considerations for analysis and wave-front sensing / Vorontsov M.A., Kolosov V.V. //J. Opt. Soc. Amer. A. 2005. V. 22. №1. P. 126-141.
13. Колосов В.В. Уравнение переноса излучения в опи-сании ветровой рефракции частично-когерентных пучков / Колосов В.В., Кузнецов М.Ф. //Оптика атмосферы и океана. 1989. Т. 2. № 5. С. 462-473.
14. Землянов А.А. Влияние нелинейных и флуктуационных искажений пучка на процесс просветления жидкокапельной среды при регулярном режиме испарения капель / Землянов А.А., Кузиковский А.В. //V Всесоюзный симпозиум по распространению лазерного излучения в атмосфере. Тезисы докладов. Часть III. Томск, 1979. С. 69-75.

Список литературы на английском языке / References in English

1. Rytov S.M. Vvedenie v statisticheskuyu radiofiziku [Introduction to Statistical Radiophysics] / Rytov S.M., Kravtsov Yu.A., Tatarskii V.I. – : Nauka, 1978. 463 p. [in Russian]
2. Kandidov V.P. O primenenii metoda statisticheskikh ispyta-nii k issledovaniyu rasprostraneniya volnovogo puchka v sluchaino-neodnorodnoi srede [On Application of Statistical Test Method to the Study of Wave Ray Propagation in a Randomly Inhomogeneous Medium] / Kandidov V.P., Ledenev V.I. // Izv. vuzov. Radiofiz [Bulletin of Universities. Ra-diophys]. 1981. V. 24. No.4. P. 438-442. [in Russian]
3. Konyaev P.A. Modifikatsiya metoda rasshchepleniya dlya chislennogo re-sheniya kvaziopticheskikh zadach [Modification of Splitting Method for Numerical Solu-tion of Quasi-optical Problems] / Konyaev P.A. // VI Vses. simpoz. po rasprostraneniyu lazernogo izluche-niya v atmosfere. Chast' III [VI All-Union Symposium on Propagation of Laser Radiation in Atmosphere. Part III]. Tomsk, 1981. P. 195-198. [in Russian]
4. Pasmanik G.A. Samovozdeistvie puchkov nekogerentnogo sveta [Self-action of Incoherent Light Rays] / Pasmanik G.A. // ZhETF [Journal of Experimental and Theoretical Phys-ics]. 1974. V. 66. No. 2. P. 490-500. [in Russian]
5. Aleshkevich V.A. Samovozdeistvie neko-gerentnogo svetovogo puchka [Self-action of Incoherent Light Ray] / Aleshkevich V.A., Lebedev S.S., Matveev A.N. // Kvantovaya elektro-nika [Quantum Electronics]. 1981. V. 8. No. 5. P. 1090-1094. [in Russian]
6. Dolin L.S. O luchevom opisanii slabo-neodnorodnykh volnovykh polei [On Ray Description of Weakly Inhomogeneous Wave Fields] / Dolin L.S. // Izv. vyssh. uchebn. zavedeniy. Radiofizika [Bulletin of Universities. Radiophys]. 1964. V. 7. No. 3. P. 559-562. [in Russian]
7. Rytov S.M. Vvedenie v statisticheskuyu radiofiziku [Introduction to Statistical Radiophysics] / Rytov S.M., Kravtsov Yu.A., Tatarskij V.I. Part II Random Fields. – : Nauka, 1978. 463 p. [in Russian]
8. Kolosov V.V. O fazovoi kompensatsii refraktsionnykh iskazhenii chastichno kogerentnykh puchkov [On Phase Compensation of Refractive Dis-tortions of Partially Coherent Rays] / Kolosov V.V., Kuzikovskii A.V. // Kvantovaya elektronika [Quantum Electronics\. 1981. V. 8. No. 3. P. 490-494. [in Russian]
9. Dudorov V.V. Korrektsiya nekogerentnykh izobrazhenii obiektov v usloviyakh anizoplanatizma turbulentnosti po opornomu istochniku izlucheniya razlichnoi dliny volny [Correction of Incoherent Images of Objects under Conditions of Anisoplanatism Turbulence by Reference Radiation Source of Various Wavelengths] / Dudorov V.V., Kolosov V.V. // Optika atmosfery i okeana [Optics of Atmosphere and Ocean]. 2010. V. 23. No. 5. P. 392-397. [in Russian]
10. Akhmanov S.A. Statisticheskaya radiofizika i optika. Sluchainye kolebaniya i volny v lineinykh sistemakh [Statistical Radiophysics and Optics. Random Vibrations and Waves in Linear Systems] / Akhmanov S.A., Dyakov Yu.E., Chirkin A.S. M.: Fizmatlit, 2010. 446 p. [in Russian]
11. Vorobiev V.V. Ushirenie svetovogo puchka v nelineinoi srede so slu-chainymi neodnorodnostyami pokazatelya prelomleniya [Light Ray Broadening in Nonli-near Medium with Random Inhomogeneities of the Refractive Index] / Vorobiev V.V. // Izv. vuzov. Radiofiz [Bulletin of Universities. Radiophys]. 1970. V. 13.P. 1053-1060. [in Russian]
12. Vorontsov M.A. Target-in-the-loop beam control: basic considerations for analysis and wave-front sensing / Vorontsov M.A., Kolosov V.V. //J. Opt. Soc. Amer. A. 2005. V. 22. №1. P. 126-141.
13. Kolosov V.V. Uravnenie perenosa izlucheniya v opi-sanii vetrovoi refraktsii chastichno-kogerentnykh puchkov [Radiation Transfer Equation in the Description of Wind Refraction of Partially Coherent Rays] / Kolosov V.V., Kuznetsov M.F. // Optika atmosfery i okeana [Optics of Atmosphere and Ocean]. 1989.Vol. 2. No. 5. P. 462-473. [in Russian]
14. Zemlyanov A.A. Vliyanie nelineinykh i fluktuatsion-nykh iskazhenii puchka na process prosvetleniya zhidkokapelnoj sredy pri regulyarnom rezhime ispareniya kapel [Influence of Nonlinear and Fluctuation Distortions of Ray on the Process of Liquid-drop Medium Lucency with a Regular Mode of Droplet Evaporation] / Zemlyanov A.A., Kuzikovskii A.V. // V Vsesoyuznyy simpozium po rasprostraneniyu lazernogo izlucheniya v atmosfere. Tezisy dokladov. Chast' III [V All-Union Symposium on the Propagation of Laser Radiation in the Atmosphere. Abstracts of Reports. Part III. Tomsk], 1979. P. 69-75. [in Russian]