МОДЕЛЬ ХИЩНИК-ЖЕРТВА НА ЛИНЕЙНОМ АРЕАЛЕ
МОДЕЛЬ ХИЩНИК-ЖЕРТВА НА ЛИНЕЙНОМ АРЕАЛЕ
Научная статья
Гончарова А.Б.1, *, Данилова М.Ю.2, Колпак Е.П.3
1,2,3Санкт-Петербургский государственный университет,Санкт-Петербург, Россия
* Корреспондирующий автор (a.goncharova[at]spbu.ru)
АннотацияПроводится исследование математической модели хищник-жертва RosenzweigM.G. и MacArthurR.H. на отрезке прямой. Дан анализ стационарных решений, получены условия существования периодических по пространственной переменной решений. Приведены варианты возможных распределений численностей хищников и жертв на территории. Модель расширена для взаимодействия популяций в условиях антропогенного давления. В основе модели лежат статистические данные по загрязненной территории в окрестности медно-никелевого комбината. Дана оценка возможного уменьшения численности популяций хищника и жертвы в зависимости от степени загрязнения. С применением имитационного моделирования построены распределения хищников и жертв в зависимости от антропогенной нагрузки.
Ключевые слова: математическое моделирование, устойчивость, загрязнение, популяция, хищник, жертва.
PREDATOR-PREY MODEL ON A LINEAR TERRITORY
Research article
Goncharova A.B.1, *, Danilova M.Yu.2, Kolpak E.P.3
1,2,3St. Petersburg State University,Saint Petersburg, Russia
* Corresponding author (a.goncharova[at]spbu.ru)
AbstractThe current article carries out a study of the Rosenzweig-MacArthur predator-prey model on a straight line segment. The authors provide an analysis of stationary solutions and obtain the conditions for the existence of periodic solutions in a spatial variable. The study provides variants of possible distributions of the numbers of predators and victims in the territory. The model is extended for the interaction of populations under anthropogenic pressure. It is also based on statistical data on the contaminated area in the vicinity of a copper-nickel plant. The research features an assessment of the possible decrease in the number of predator and prey populations depending on the degree of contamination. With the use of simulation modeling, the study constructs the distributions of predators and victims depending on the anthropogenic load.
Keywords: mathematical modeling, sustainability, pollution, population, predator, prey. ВведениеРазвитие промышленного и сельскохозяйственного производства последние несколько столетий сопровождаются усилением антропогенного давления на природную среду. Вредные для всего живого вещества в виде тяжелых металлов и химических соединений выбрасываются различными предприятиями в окружающую среду, загрязняя обширные территории [1], [2], [3]. На освоенных человеком территориях изменяется флора и фауна, фрагментируется среда обитания, разрываются трофические цепи [4], [5], уменьшаются объемы трофических ресурсов.
Загрязняющие окружающую среду тяжелые металлы и химические соединения обладают способностью накапливаться в живых организмах, не разлагаются, способны длительное время циркулировать в биологических системах [6]. Циркуляция в экосистемах загрязняющих веществ приводит к постепенной деградации среды обитания, гибели или исчезновению живых организмов в пораженных загрязнителями зонах [7], [8]. В организмах животных и растений токсиканты вызывают нарушение многих биохимических функций в клетках организмов. Все это приводит к тяжелым поражениям жизненно важных органов и нервной системы, а также отрицательно влияет на наследственность [7], [8]. Накопленные у одних организмов вещества через трофические цепи поступают в другие организмы.
Математические модели взаимодействующих популяций в своем большинстве [9] не учитывают влияние на их динамику внешних факторов, вызванных антропогенным давлением. Одним из видов взаимодействия является хищник-жертва.
Математическая модель хищник-жертва
В первой математической модели хищник-жертва Вольтерра не учитывались ограниченность трофического ресурса жертвы и изобилие жертв для хищников [9]. В отсутствие хищника модель прогнозирует неограниченный рост численности жертвы. Вместе с этим скорость убыли жертвы в случае ее изобилия не должна значительно зависеть от ее численности, а должна зависеть только от численности хищника. Эти факторы учитываются в модели RosenzweigM.G. и MacArthurR.H. [10], [11], [12]. Для случая взаимодействия хищников и жертв на прямой модель представлена системой дифференциальных уравнений в частных производных
 |
(1) |
где u ‑ линейная плотность жертв, v‑ линейная плотность хищников, a, b, g‑ параметры, характеризующие скорости размножения и гибели хищников и жертв Du и Dv, и коэффициенты, характеризующие подвижность жертв и хищников на линейном ареале. Система уравнений (1) получена в [9] в предположениях, что удельная скорость размножения жертв равна единице и единичной емкости среды.
Слагаемое u(1-u) в первом уравнении системы уравнений (1) – скорость роста численности популяции жертв в отсутствие хищников, а слагаемое ![]() ‑ скорость уничтожения жертв хищниками. Во втором уравнении слагаемое gv‑ скорость естественной гибели хищников, а слагаемое
‑ скорость уничтожения жертв хищниками. Во втором уравнении слагаемое gv‑ скорость естественной гибели хищников, а слагаемое ![]() ‑ скорость роста популяции хищников за счет уничтожения ими жертв.
‑ скорость роста популяции хищников за счет уничтожения ими жертв.
Общее количество хищников и жертв на отрезке длиной l подсчитывается по формулам
 К системе уравнений (1) добавляются начальные условия
при t= 0: u=u0 (0, x), v=v0(t,x),
и граничные условия
К системе уравнений (1) добавляются начальные условия
при t= 0: u=u0 (0, x), v=v0(t,x),
и граничные условия
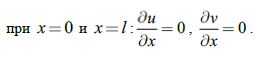 |
(2) |
 |
(3) |
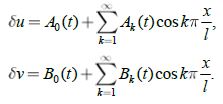 |
(4) |

При любом малом начальном положительном возмущении du = du0 (t= 0, x) и dv = dv0 (t= 0, x) тривиального решения системы уравнений (3) A0(t) будет возрастающей функцией времени, функции Ak (t) (k = 1,..) могут быть как возрастающими, так и убывающими. Функции Bkt при любых k = 0,1... будут убывающими функциями. То есть решение u=0, v=0 будет неустойчивым – численность жертвы будет увеличиваться.
В окрестности стационарного решения u=1, v=0 , система уравнений для возмущений приводится к виду
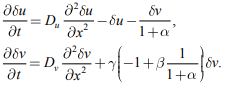 |
(5) |

При выполнении неравенства b< 1 + a все функции Bk(t) и Ak (t) при любых k = 0,1... будут убывающими функциями времени, а при нарушении этого неравенства возрастающей функцией будет функция B0(t) - то есть эта стационарное состояние в этом случае будет неустойчивым.
Неравенство b< 1 + a соответствует малому «поеданию» [9] жертвы хищником (большие значения параметра) или медленной «переработке» жертвы хищником (малые значения параметра b).
При выполнении неравенства b> 1 +a возрастающими будут те Bk(t), для которых выполняется неравенства
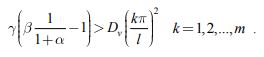
В этом случае, как следует из системы уравнений (5), распространение хищника на территории может сопровождаться образованием неоднородного распределения его численности на отрезке.
Нетривиальное стационарное решение, на котором 0 < u и 0 < v находится из системы алгебраических уравнений
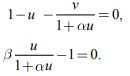 Решением этой системы уравнений являются
Решением этой системы уравнений являются
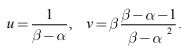 Физический смысл это решение имеет при выполнении неравенства b> 1 + a. То есть скорость переработки хищником жертвы должна быть значительно больше, чем удельная скорость его гибели.
Малые возмущения du = du0 (t= 0, x) и dv = dv0 (t= 0, x) этого положения равновесия с точностью до величин второго порядка малости удовлетворяют уравнениям
Физический смысл это решение имеет при выполнении неравенства b> 1 + a. То есть скорость переработки хищником жертвы должна быть значительно больше, чем удельная скорость его гибели.
Малые возмущения du = du0 (t= 0, x) и dv = dv0 (t= 0, x) этого положения равновесия с точностью до величин второго порядка малости удовлетворяют уравнениям
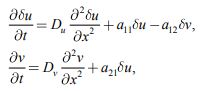 |
(6) |
 Поиск решения системы уравнений (6) в виде тригонометрических рядов (4) приводит к системе уравнений (k= 0, 1, 2,...)
Поиск решения системы уравнений (6) в виде тригонометрических рядов (4) приводит к системе уравнений (k= 0, 1, 2,...)
 |
(7) |
 осуществлялось с применением конечно-разностного метода.
осуществлялось с применением конечно-разностного метода.
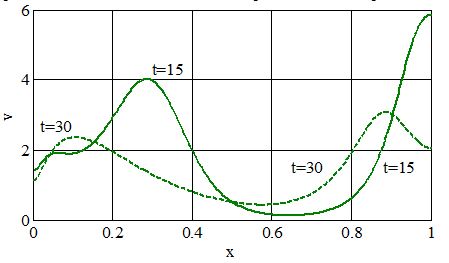
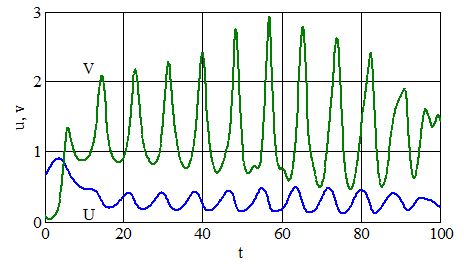
Решение в виде зависимостей u = u(t,x), в моменты времени t= 15 и t= 30 приведено на рис. 1, а для зависимости v = v (t,x)‑ на рис. 2. Изменение во времени общего количества жертв (U(t)) и хищников (V(t)) приведено на рис. 3. Зависимости приведены при значениях параметров a = 3, b= 6.5, g= 2, Du = 0.0001, Dv = 0.0001. Подвижность жертв (Du) принята значительно меньшей, чем подвижность хищников (Dv). Решение строилось на пространственной сетке с 500 отрезками разбиения. При увеличении числа отрезков разбиения до 1 000 результаты отличались не более чем на 1.5% в максимальных отклонениях.
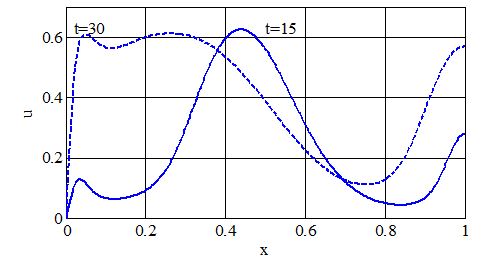
Рис. 1 – Распределение плотности численности жертвы в моменты времени t= 15 и t= 30
Рис. 2 – Распределение плотности численности хищника в моменты времени t= 15 и t= 30
Рис. 3 – Изменение общего количества жертв и хищников во времени
Антропогенное давлениеОт источников загрязнения загрязняющие вещества распространяются на значительные расстояния. Наибольшее их количество выпадает в окрестности источников [13], [14]. Совокупный вынос загрязнителей при условии прекращения новых поступлений из антропогенных источников может длиться несколько десятилетий, а период естественного самоочищения водных и наземных экосистем от загрязняющих веществ оценивается в сотни лет. Один из вариантов распределения тяжелых металлов в окрестности Мончегорского (Мурманская область) медно-никелевого комбината приведен на рис. 4 в виде зависимости концентрации меди ( Cu) и никеля (Ni ) на почве (гр металлов в кг почвы) в зависимости от расстояния до комбината [13]. Символами «о» и «*» отмечены статистические данные полевых наблюдений. Как следует из анализа этих данных они аппроксимируются экспоненциальными зависимостями ![]() (на рис. 4 сплошные линии) с показателям m = 0.1 как для Cu, так и для Ni. Эти показатели могут изменяться в зависимости от направления распространения металлов от источника загрязнения.
(на рис. 4 сплошные линии) с показателям m = 0.1 как для Cu, так и для Ni. Эти показатели могут изменяться в зависимости от направления распространения металлов от источника загрязнения.
Накопление металлов в организмах животных и растениях пропорционально количеству металлов в окружающей среде [15]. Поглощенное живыми организмами количество загрязнителей убывает против градиента концентрации загрязнителей.
Рис. 4 – Распределение концентрации меди и никеля в почве в зависимости от расстояния от комбината
Таким образом, накопление металлов организмами сопровождается изменением рождаемости, а накопление на территории обитания приводит к уменьшению трофической емкости среды [9]. Учитывая характер изменения концентраций металлов (рис. 4) принимается, что и накопление металлов в организмах уменьшается по экспоненциальной зависимости при удалении от точки выброса, а емкость среды увеличивается. Таким образом, наименьшая рождаемость жертв около точки выброса, и возрастает на удалении от источника выбросов по экспоненциальной зависимости. Накоплением металлов хищниками пренебрегается. С учетом этих предположений модель антропогенного давления на систему хищник-жертва представлена (с учетом (1)) системой уравнений
 которые предполагают, что в точке x=0 максимальная концентрация загрязнителей, при которой жертва жить не может. Хищник в поисках жертвы может находиться в любой точке отрезка.
В качестве начальных условий принимается, что жертва распределена по отрезку по закону синуса:
которые предполагают, что в точке x=0 максимальная концентрация загрязнителей, при которой жертва жить не может. Хищник в поисках жертвы может находиться в любой точке отрезка.
В качестве начальных условий принимается, что жертва распределена по отрезку по закону синуса:

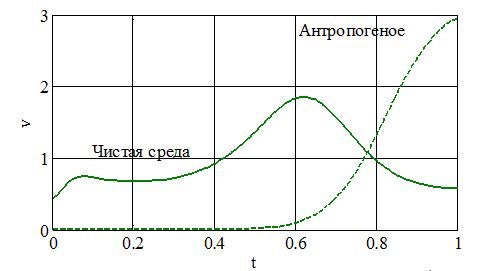
На рис. 5 приведено распределение жертвы на отрезке в момент времени t= 30 для случая параметров a = 3, b= 6.5, g= 2, Du = 0.0001, Dv = 0.0001, m1= 0.5, m2= 1 (пунктирная линия), а на рис. 6 – распределение хищника (пунктирная линия, «антропогенное»). Сплошные линии на рис. 5 и рис. 6 соответствуют распределению жертвы и хищника для случая m1= 0 и m2= 0 («чистая среда»). Построение численного решения системы уравнений (8) осуществлялось с применением метода сеток.

Рис. 5 – Распределение жертвы на отрезке на загрязненной территории («антропогенное») и на не загрязненной территории («чистая среда») в момент времени t= 30
Рис. 6 – Распределение хищника на отрезке на загрязненной территории («антропогенное») и на не загрязненной территории («чистая среда») в момент времени t= 30
Как следует из этих результатов хищник «уходит» на значительные расстояния от источника загрязнения (рис. 6) в отличие от жертвы (рис. 5). Имитационная модельИмитационное моделирование распределения общего количества хищников и жертв на отрезке при различных уровнях загрязнения осуществляется путем случайного выбора параметров m1 и m2 из заданного диапазона. Расчет для N комбинаций m1 и m2 позволяет оценить распределение численности хищников и жертв при антропогенном давлении.
На рис. 7 приведено стационарное распределение общего количества жертв, а на рис. 8 – хищников для 1 000 вариантов случайного выбора m1O( 0.1, 1) и m2O(0,2). Вертикальными пунктирными линиями отмечены стационарные численности в отсутствие загрязнения. При выбранном наборе изменения антропогенной нагрузки среднее значение хищников на отрезке уменьшается в четыре раза, а жертв – в три раза.
Рис. 7 – Распределение общего количества численности жертв на единичном отрезке для 1000 вариантов случайного выбора параметров m1 и m2
Рис. 8 – Распределение общего количества численности хищников на единичном отрезке для 1000 вариантов случайного выбора параметров m1 и m2
Как следует из рис. 7 и рис. 8 общая численность жертв и хищников на отрезке при антропогенном давлении уменьшается по сравнению с общим их количеством в «чистой» среде. При этом происходит сдвиг численности в зоны с меньшей антропогенной нагрузкой.
Заключение
Модель динамического взаимодействия хищника и жертвы прогнозирует неоднородное распределение особей на территории с возможным возникновением периодических по пространству структур. Антропогенное давление, вызывающее изменение внутреннего метаболизма особей и уменьшающее емкость среды, вызывает уменьшение общей численности и хищников и жертв. Наибольшие потери может понести хищник.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
- Касиков А. Г. Пылевые выбросы медно-никелевого производства и последствия их воздействия на организм человека в условиях крайнего севера / А. Г. Касиков // Вестник Кольского научного центра РАН. – 2017. ‑ 4(10). ‑ С. 58-63.
- Девяткин П.Н. Природные водные ресурсы района г. Мончегорск в условиях функционирования ОАО "Кольская горно-металлургическая компания" / П.Н. Девяткин //Вестник МГТУ. – 2008. – Т. 11. ‑ №3.– С. 393-397.
- Кин Н.О. Растительные сообщества в зоне промышленной разработки газа и аккумуляция ими тяжелых металлов / Н.О. Кин // Экология. ‑ 2008. ‑ № 4. ‑ С. 269-275.
- Пегов А.С. Антропогенное воздействие на биосферу / А.С. Пегов // Труды ИСА РАН. ‑ 2009. ‑ Т. 42. ‑ С.5-32.
- Ярмишко В. Т. Многолетний импактный мониторинг состояния сосновых лесов в центральной части Кольского полуострова / В. Т.Ярмишко, О. В. Игнатьева // Известия РАН. Серия биологическая. – 2019. ‑ № 6. ‑ С. 658–668. DOI: 1134/S0002332919060134.
- Кашулина Г. М. Мониторинг загрязнения почв тяжелыми металлами в окрестностях медно-никелевого предприятия на Кольском полуострове / Г. М. Кашулина // Почвоведение. ‑ 2018. ‑ № 4. ‑ С. 493–505.
- Моисеенко Т. И. Биодоступность и экотоксичность металлов в водных системах: критические уровни загрязнения / Т. И. Моисеенко // Геохимия. ‑2019. ‑ Т. 64. ‑ № 7. ‑ С.675–688. DOI: 31857/S0016-7525647675-688.
- Мухачева С. В. Химическое загрязнение среды: тяжелые металлы в пище мелких млекопитающих / С. В. Мухачева, В. С. Безель // Зоологический журнал. ‑ 2007. ‑ Т. 86. ‑ № 4. ‑ С.492-498.
- Базыкин А.Д. Нелинейная динамика взаимодействующих популяций / А.Д.Базыкин. – Москва-Ижевск, Институт компьютерных исследований, 2003. 368 с.
- Rosenzweig M.G. Graphical representation and stability conditions of predator-prey interactions /M.G.Rosenzweig, R.H. MacArthur // Amer. Natur. ‑ 1963. ‑ V. 97. ‑ № 893. ‑ P. 209-223.
- ЦибулинВ. Г. Нелинейная динамика системы хищник–жертва на неоднородном ареале и сценарии локального взаимодействия видов /В. Г.Цибулин, Т. Д.Ха, П. А. Зеленчук // Известия высших учебных заведений. Прикладная нелинейная динамика. ‑ 2021. ‑ Т. 29. ‑ № 5. ‑ С. 751–764. DOI: 10.18500/0869-6632-2021-29-5-751-764.
- Абрамова Е.П. Динамические режимы стохастической модели «хищник – жертва» с учетом конкуренции и насыщения / Е.П.Абрамова, Т.В. Рязанова // Компьютерные исследования и моделирование. – 2019. ‑ Т. 11. ‑ № 3. ‑ С. 515–531. DOI: 10.20537/2076-7633-2019-11-3-515-531.
- Опекунова М.Г. Мониторинг изменения окружающей среды в зоне воздействия комбината «Североникель». II Миграция и аккумуляция химических элементов в почвах / М.Г.Опекунова, Е.Ю.Елсукова, В.А.Чекушин и др. // Вестник СПбГУ. Сер. 7. ‑ 2006. ‑ Вып. 3. ‑ С. 39-49.
- Елсукова Е.Ю. Техногенная трансформация потоков тяжелых металлов в почвах в зоне воздействия медно-никелевого производства / Е.Ю.Елсукова,М.Г.Опекунова, А.Ю. Опекунов // Международный научно-исследовательский журнал. – 2019. ‑№ 12-1 (90). ‑ С. 118-124. DOI: 10.23670/IRJ.2019.90.12.024.
- Ивантер Э. В. Влияние техногенных загрязнений на популяции мелких лесных грызунов / Э. В.Ивантер, Н. В. Медведев // Доклады академии наук,‑ 2015. – Т. 464. ‑ № 6. ‑ С. 758–761. DOI: 7868/S0869565215300271.
Список литературы на английском языке / ReferencesinEnglish
- Kasikov A. G. Pylevye vybrosy medno-nikelevogo proizvodstva i posledstvija ikh vozdejjstvija na organizm cheloveka v uslovijakh krajjnego severa [Dust emissions of copper-nickel production and the consequences of their impact on the human body in the conditions of the Far North] / A. G. Kasikov // Vestnik Kol'skogo nauchnogo centra RAN. [Bulletin of the Kola Scientific Center of the Russian Academy of Sciences]. - 2017. ‑4(10). ‑pp. 58-63 [in Russian]
- Devyatkin P.N. Prirodnye vodnye resursy rajjona g. Monchegorsk v uslovijakh funkcionirovanija OAO "Kol'skaja gorno-metallurgicheskaja kompanija" [Natural water resources of the district of Monchegorsk in the conditions of functioning of JSC "Kolskaya Mining and Metallurgical Company" / P. N. Devyatkin // Vestnik MGTU [Bulletin of the Moscow State Technical University]. - 2008. - Vol. 11. ‑No. 3. - pp. 393-397 [in Russian]
- Kin N.O. Rastitel'nye soobshhestva v zone promyshlennojj razrabotki gaza i akkumuljacija imi tjazhelykh metallov [Plant communities in the zone of industrial gas development and their accumulation of heavy metals] / N. O. Kin // Ekologiya [Ecology]. ‑2008. ‑No. 4. ‑pp. 269-275 [in Russian]
- Pegov A.S. Antropogennoe vozdejjstvie na biosferu [Anthropogenic impact on the biosphere] / A. S. Pegov // Trudy ISA RAN [Proceeding of the Institute for Systems Analysis of the Russian Academy of Science]. ‑ 2009. ‑Vol. 42. ‑pp. 5-32 [in Russian]
- Yarmishko V. T. Mnogoletnijj impaktnyjj monitoring sostojanija sosnovykh lesov v central'nojj chasti Kol'skogo poluostrova [Long-term impact monitoring of pine forests in the central part of the Kola Peninsula] / V. T. Yarmishko, V. Ignatyeva // Izvestija RAN. Serija biologicheskaja [News of the Russian Academy of Sciences. The series is biological]. – 2019. ‑No. 6. ‑pp. 658-668. DOI: 10.1134/S0002332919060134 [in Russian]
- Kashulina G. M. Monitoring zagrjaznenija pochv tjazhelymi metallami v okrestnostjakh medno-nikelevogo predprijatija na Kol'skom poluostrove [Monitoring of soil pollution by heavy metals in the vicinity of a copper-nickel enterprise on the Kola Peninsula] / G. M. Kashulina // Pochvovedenie [Soil Science]. ‑2018. ‑No. 4. ‑pp. 493-505 [in Russian]
- Moiseenko T. I. Biodostupnost' i ehkotoksichnost' metallov v vodnykh sistemakh: kriticheskie urovni zagrjaznenija [Bioavailability and ecotoxicity of metals in water systems: critical pollution levels] / T. I. Moiseenko // Geokhimija [Geochemistry]. – 2019. 64. No. 7. pp. 675-688. DOI: 10.31857/S0016-7525647675-688 [in Russian]‑‑‑‑
- Mukhacheva S.V. Bezel V.S. Khimicheskoe zagrjaznenie sredy: tjazhelye metally v pishhe melkikh mlekopitajushhikh [Chemical pollution of the environment: heavy metals in the food of small mammals] / S. V. Mukhacheva, V. S. Bezel // Zoologicheskijj zhurnal [Zoological Journal]. Vol. 86. No. 4. pp.492-498 [in Russian]
- Bazykin A.D. Nelinejjnaja dinamika vzaimodejjstvujushhikh populjacijj [Nonlinear dynamics of interacting populations] / A. D. Bazykin. - Moscow-Izhevsk, Institute of Computer Research, 2003. 368 p. [in Russian]
- Rosenzweig M.G., MacArthur R.H. Graphical representation and stability conditions of predator-prey interactions // Amer. Natur. ‑ 1963. ‑ V. 97. ‑ № 893. ‑ P. 209-223. [in Russian]
- Tsybulin V. G. Nelinejjnaja dinamika sistemy khishhnik–zhertva na neodnorodnom areale i scenarii lokal'nogo vzaimodejjstvija vidov [Nonlinear dynamics of the predator-prey system on an inhomogeneous area and scenarios of local interaction of species] / V. G. Tsybulin, T. D. Kha, P. A. Zelenchuk // Izvestija vysshikh uchebnykh zavedenijj. Prikladnaja nelinejjnaja dinamika [Izvestia of Higher educational institutions. Applied nonlinear dynamics]. ‑ 2021. ‑Vol. 29. ‑No. 5. ‑ 751-764. DOI: 10.18500/0869-6632-2021-29-5-751-764 [in Russian]
- Abramova E.P. Dinamicheskie rezhimy stokhasticheskojj modeli «khishhnik – zhertva» s uchetom konkurencii i nasyshhenija [Dynamic modes of the stochastic predator - prey model taking into account competition and saturation] / P. Abramova, T. V. Ryazanova // Komp'juternye issledovanija i modelirovanie [Computer research and modeling]. – 2019. ‑Vol. 11. ‑No. 3. ‑pp. 515-531. DOI: 10.20537/2076-7633-2019-11-3-515-531 [in Russian]
- OpekunovaM.G. Monitoringizmenenijaokruzhajushhejjsredyvzonevozdejjstvijakombinata «Severonikel'». II Migracija i akkumuljacija khimicheskikh ehlementov v pochvakh [Monitoring of environmental changes in the impact zone of the Severonikel Plant. II Migration and accumulation of chemical elements in soils] / M. G. Opekunova, E. Yu. Yelsukova, A. Chekushin, et al. // Vestnik SPbGU [Vestnik Of Saint Petersburg University. Series 7]. ‑2006. ‑Issue 3. ‑ pp. 39-49 [in Russian]
- Yelsukova E.Yu. Tekhnogennaja transformacija potokov tjazhelykh metallov v pochvakh v zone vozdejjstvija medno-nikelevogo proizvodstva [Technogenic transformation of heavy metal flows in soils in the zone of impact of copper-nickel production] / E. Yu. Yelsukova, M. G. Opekunova, A. Yu. Opekunov // Mezhdunarodnyjj nauchno-issledovatel'skijj zhurnal [International Research Journal] – 2019. ‑No. 12-1 (90). ‑pp. 118-124. DOI: https://doi.org/10.23670/IRJ.2019.90.12.024 [in Russian]
- Ivanter E. V. Vlijanie tekhnogennykh zagrjaznenijj na populjacii melkikh lesnykh gryzunov [Influence of technogenic pollution on populations of small forest rodents] / E. V. Ivanter, N. V. Medvedev // Doklady akademii nauk [Proceedings of the Academy of Sciences], ‑2015. - Vol. 464. ‑No. 6. ‑pp. 758-761. DOI: 10.7868/S0869565215300271 [in Russian]