МАТРИЧНОЕ ИСЧИСЛЕНИЕ В АЛГЕБРЕ ЛОГИКИ
МАТРИЧНОЕ ИСЧИСЛЕНИЕ В АЛГЕБРЕ ЛОГИКИ
Научная статья
Сдвижков О.А.1, *, Мацнев Н.П.2
1 Российский государственный университет туризма и сервиса, Пушкино, Россия;
2 Технологический университет, Королев, Россия
* Корреспондирующий автор (oasdv[at]yandex.ru)
АннотацияПрименяя операцию сложения по модулю два, в алгебре логики определяются фундаментальные понятия матричного исчисления, такие как линейно зависимые и независимые совокупности строк (столбцов) матрицы, ранг матрицы, сумма и произведение матриц, определитель матрицы, обратная матрица. Приводятся свойства определителей алгебры логики. С помощью обратных матриц алгебры логики решаются системы линейных уравнений с суммами по модулю два. Приведены примеры на вычисление в алгебре логики ранга матрицы, определителей, обратных матриц и решение систем линейных уравнений с суммами по модулю два.
Ключевые слова: бинарная матрица, сумма по модулю два, определитель, обратная матрица, ранг матрицы, система уравнений.
MATRIX CALCULATION IN LOGIC ALGEBRA
Research article
Sdvizhkov O.A.1, *, Matsnev N.P.2
1 Russian State University of Tourism and Service, Pushkino, Russia;
2 University of Technology, Korolev, Russia
* Corresponding author (oasdv[at]yandex.ru)
AbstractUsing the modulo two addition operation, the fundamental concepts of matrix calculus are defined in the logic algebra, such as linearly dependent and independent sets of rows (columns) of a matrix, matrix rank, sum and product of matrices, matrix determinant, inverse matrix. The properties of the determinants of the logic algebra are given. Using inverse matrices of the logic algebra, systems of linear equations with modulo two sums are solved. Examples are given for calculating the rank of a matrix, determinants, inverse matrices and solving systems of linear equations with modulo two sums in the logic algebra.
Keywords: binary matrix, modulo two sum, determinant, inverse matrix, matrix rank, system of equations.
Введение
Алгебра логики, в широком смысле, которого придерживаются авторы, это раздел математики, построенный на множестве Е2 = {0, 1}.
Некоторые проблемы алгебры логики рассматривались одним из авторов в работах [6], [7], [8], данная статья посвящена формулам алгебры логики, позволяющим выполнять матричные операции.
Фундаментальные формулы матричного исчисления [2], [3], [5] во множестве матриц алгебры логики не имеют смысла, так как в алгебре логики нет операций +, – и так далее, применяемых в этих формулах, как и других чисел кроме 0 и 1.
В статье показывается, что, применяя сложение по модулю два, формулы матричного исчисления можно заменить формулами алгебры логики, корректно выполняющими матричные операции.
1. Простейшие операции с булевыми матрицамиПусть задана матрица ![]() . Такая матрица называется булевой (бинарной, двоичной, матрицей алгебры логики).
. Такая матрица называется булевой (бинарной, двоичной, матрицей алгебры логики).
Матрицу ![]() , где
, где ![]() – бинарное число, противоположное числу
– бинарное число, противоположное числу ![]() , естественно назвать противоположной матрице А.
, естественно назвать противоположной матрице А.
Произведение матрицы А на константу ![]() определяется обычным образом:
определяется обычным образом:
Под суммой матриц А и В вида m×n в алгебре логики, естественно, понимать матрицу , элементы которой находятся по формуле:
![]()
Назовем булевым (бинарным) произведением матрицы вида m×p на матрицу вида p×n такую матрицу С вида m×n, обозначаемую А*B mod 2, элементы которой находятся по формуле:
 где все коэффициенты принимают значения из множества Е2.
Столбцы j1, j2, …, jr назовем бинарно линейно независимыми, если
где все коэффициенты принимают значения из множества Е2.
Столбцы j1, j2, …, jr назовем бинарно линейно независимыми, если
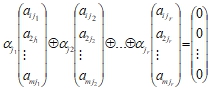 выполняется только при
выполняется только при 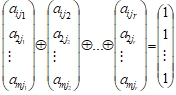 Пусть столбцы j1, j2, …, jr бинарно линейно зависимые, причем, например,
Пусть столбцы j1, j2, …, jr бинарно линейно зависимые, причем, например, 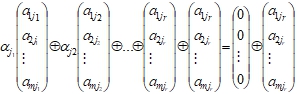 Откуда следует, что столбец jr является бинарной линейной комбинацией остальных столбцов:
Откуда следует, что столбец jr является бинарной линейной комбинацией остальных столбцов:
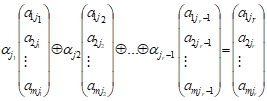 Пусть столбцы j1, j2, …, jr сильно независимые. Тогда можно записать:
Пусть столбцы j1, j2, …, jr сильно независимые. Тогда можно записать:
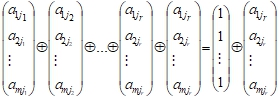
Откуда следует, что столбец противоположный столбцу jr, как и любому другому столбцу, является бинарной линейной комбинацией остальных столбцов:
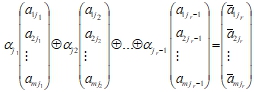
Понятно, что аналогичные определения и рассуждения имеют место и для строк матрицы А.
Назовем булевым рангом матрицы А, обозначим его rang*(A), максимальное число бинарно линейно независимых столбцов (строк) матрицы А.
2. Булевы определители и их свойстваНазовем булевым (бинарным) определителем квадратной матрицы n-го порядка ![]() величину
величину
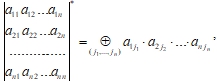
где суммирование по модулю 2 выполняется по всем попарно различным значениям индексов j1, j2,…, jn. Звездочка справа показывает, что величина определителя рассчитывается по формуле, отличной от применяемой во множестве R. Этот определитель будем обозначать также |A|* или Δ*.
В силу данного определения, разложение определителя |A|* по i-й строке имеет вид
![]()
а разложение по j-му столбцу записывается в виде
![]()
Mij – бинарный определитель матрицы, получаемой вычеркиванием i-й строки и j-го столбца из матрицы А.
Примеры:
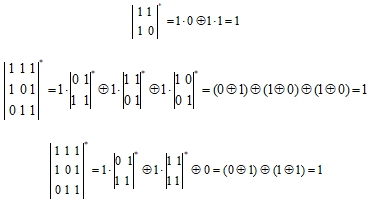
Из приведенных формул вытекают свойства бинарных определителей.
- Свойства бинарных определителей, верные для строк, справедливы и для столбцов.
- При перестановке местами строк величина бинарного определителя не изменяется.
- Если в матрице А есть нулевая строка или равные строки, то ее бинарный определитель равен нулю.
- Если в матрице А элементы какой-либо строки являются суммами по модулю 2 двух слагаемых, то бинарный определитель матрицы А равен сумме по модулю 2 двух бинарных определителей.
- Если в матрице А какая-либо строка является бинарной линейной комбинацией некоторых других строк, то бинарный определитель матрицы А равен нулю.
- Если к какой-либо строке матрицы А прибавить по модулю 2 бинарную линейную комбинацию некоторых других строк, то бинарный определитель матрицы А не изменится.
- Двоичная сумма произведений элементов какой-либо строки на дополнительные бинарные миноры элементов другой строки равна нулю:
![]()
Следует заметить, в силу свойств 2 и 6, ранг матрицы rang*(A) можно найти, переставляя строки и прибавляя по модулю 2 к элементам одной строки матрицы А элементы другой строки, чтобы ниже главной диагонали оказались нули. Например:

Теорема 1. Пусть Δ – определитель бинарной матрицы А во множестве R, | Δ | – абсолютная величина определителя Δ, | Δ | mod 2 – остаток от деления | Δ | на 2. Тогда:
| Δ | mod 2 = Δ*
Следствие 1. Если Δ = 0, то Δ* = 0, а если Δ* ≠0, то Δ ≠0.
Следствие 2. Справедлива оценка: rang*(A)≤ rang(A), rang(A) – ранг матрицы А во множестве R.
3. Обратная матрица по булевому произведениюНазовем матрицу ![]() обратной по булевому произведению для матрицы
обратной по булевому произведению для матрицы ![]() и будем обозначать ее
и будем обозначать ее ![]() – единичная матрица.
– единичная матрица.
В силу свойства 7 определителей и формулы разложения бинарного определителя по i-й строке, справедлива следующая теорема.
Теорема 2. Если бинарный определитель бинарной матрицы А равен 1, то матрица А имеет единственную обратную по булевому произведению матрицу В= ![]() , элементы которой находятся по формуле:
, элементы которой находятся по формуле:
![]()
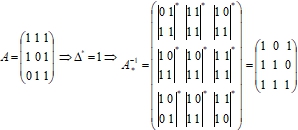 Проверка:
Проверка:
 3.
3.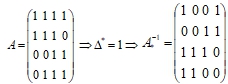 Проверка:
Проверка:
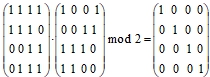 4. Системы линейных уравнений с суммами по модулю 2
Рассмотрим систему линейных уравнений с суммами по модулю 2:
4. Системы линейных уравнений с суммами по модулю 2
Рассмотрим систему линейных уравнений с суммами по модулю 2:
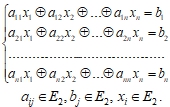
В силу теоремы 2, справедлива следующая теорема.
Теорема 3. Если определитель Δ* матрицы А системы линейных уравнений с суммами по модулю 2 равен 1, то система имеет единственное решение, которое находится по формуле:
![]()
Пример:
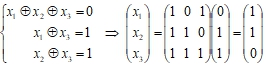
Замечание
Обратная по булевому произведению матрица к матрице системы этого примера найдена в предыдущем параграфе.
С помощью теоремы 3 доказывается следующая теорема.
Теорема 4. Если бинарный определитель матрицы системы линейных уравнений с суммами по модулю 2 равен 1, то система имеет единственное решение, которое находится по формулам, аналогичным формулам Крамера:
![]()
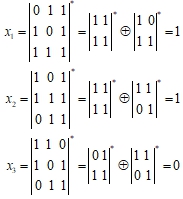 Заключение
Заключение
В статье впервые приводятся, и иллюстрируются на примерах, основные формулы матричного исчисления в алгебре логики, включая формулы решения систем линейных уравнений с суммами по модулю 2.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Гаврилов Г.П. Задачи и упражнения по дискретной математике: Учебное пособие – 3-е изд., перераб. / Г.П. Гаврилов, А.А. Сапоженко – М.: ФИЗМАТЛИТ, 2003. – 416 с.
- Андре Анго. Математика для электро- и радиоинженеров / Анго Андре – М.: Издательство «Наука», 1967. – 780 с.
- Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры / Д.В. Беклемишев – М.: Издательство «Наука», 1976. – 320 с.
- Ерусалимский Я. М. Дискретная математика: теория, задачи, приложения. 3-е издание. / Я. М. Ерусалимский – М.: Вузовская книга, 2000. – 280 с.
- Корн Г. Справочник по математике. / Г. Корн, Т. Корн – М.: Издательство «Наука», 1973. – 832 с.
- Сдвижков О. А. Дискретная математика и математические методы экономики с применением VBA Excel / О. А. Сдвижков – М.: ДМК Пресс, 2012. – 212 с.
- Сдвижков О. А. Характеристические полиномы булевых функций / Сдвижков О. А. // Международный научно-исследовательский журнал. 2017. №9-3 (63). С. 96-102
- Сдвижков О. А. Применение линейного программирования к задачам алгебры логики / Сдвижков О. А. // Международный научно-исследовательский журнал. 2017. №10-3 (64). С. 116 – 122
- Супрун В.П. Основы теории булевых функций / В.П. Супрун – М.: ЛЕНАНД, 2017. – 208 с.
- Яблонский С.В. Введение в дискретную математику: Учебное пособие для вузов / Яблонский С.В., В.А. Садовничего. – 4-е изд., стер. – М.: Высш. шк., 2003. – 384 с.
Список литературы на английском языке / References in English
- Gavrilov G.P. Zadachi i uprazhneniya po diskretnoj matematike: Uchebnoe posobie - 3-e ed., pererab. [Tasks and exercises on discrete mathematics] / G.P. Gavrilov, A.A. Sapozhenko – M.: FIZMATLIT, 2003. – 416 p. [in Russian]
- Andre Ango. Matematika dlya jelektro- i radioinzhenerov [Mathematics for elektro- and radioengineers] / Ango Andre – M.: "Science", 1967. – 780 p. [in Russian]
- Beklemishev D.V. Kurs analiticheskoj geometrii i linejnoj algebry [Rate of analytical geometry and linear algebra]/ D.V. Beklemishev – M.: "Science", 1976. – 320 p. [in Russian]
- Erusalimskij Ya. M. Diskretnaya matematika: teoriya, zadachi, prilozheniya. 3-e ed. [Discrete mathematics: the theory, task, appendix] / Ya. M. Erusalimskij – M.: high school book, 2000. – 280 p. [in Russian]
- Korn G. Spravochnik po matemamike [Mathematical handbook] / G. Korn, T. Korn – M.: "Science", 1973. – 832 p. [in Russian]
- Sdvizhkov O.A. Diskretnaja matematika i matematicheskie metody jekonomiki s primeneniem VBA Excel [Discrete mathematics and mathematical methods of economy with application VBA Excel] / O.A. Sdvizhkov – M.: DMK Press, – 212 p. [in Russian]
- Sdvizhkov O. A. Kharakteristicheskie polinomy bulevykh funktsij [Characteristic polynomials of Boolean functions] / Sdvizhkov O. A. // the International research magazine. 2017. № 9-3 (63). p. 96-102 [in Russian]
- Sdvizhkov O. A. Primenenie linejnogo programmirovaniya k zadacham algebry logiki [Application of linear programming to tasks of algebra of logic] / Sdvizhkov O. A. // the International research magazine. 2017. № 10-3 (64). p. 116 – 122 [in Russian]
- Suprun V.P. Osnovy teorii bulevykh funktsij [Bases of the theory of Boolean functions]/ V.P. Suprun – M.: LENAND, 2017. – 208 p. [in Russian]
- Yablonskij S.V. Vvedenie v diskretnuyu matematiku: Uchebnoe posobie dlya vuzov [Introduction in discrete mathematics: the manual for high schools] / Yablonskij S.V., V.A. Sadovnichego – M.: “High school”, 2003. – 384 p. [in Russian]
