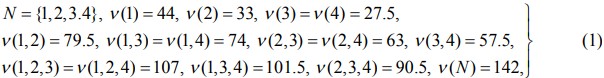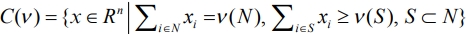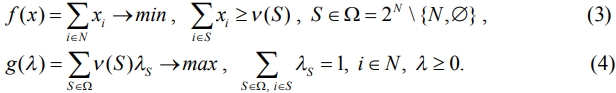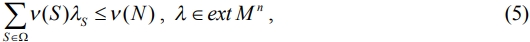КООПЕРАТИВНЫЕ ТП ИГРЫ С СИММЕТРИЧНЫМИ АГЕНТАМИ
Зинченко А.Б.
Доцент, кандидат физико-математических наук, Южный федеральный университет
КООПЕРАТИВНЫЕ ТП ИГРЫ С СИММЕТРИЧНЫМИ АГЕНТАМИ
Аннотация
Статья посвящена кооперативным играм с трансферабельными полезностями, в которых, по крайней мере, два участника симметричны. Демонстрируется техника вывода необходимых и достаточных условий существования симметричного ядра. Доказывается, что их можно использовать для доказательства пустоты С-ядра.
Ключевые слова: кооперативная ТП игра, симметричные игроки, симметричное ядро, условие существования.
Zinchenko A.B.
Assosiate professor, PhD in Physics and mathematics, Southern Federal University
COOPERATIVE TU GAMES WITH SYMMETRIC AGENTS
Abstract
The paper is devoted to cooperative transferable utility games in which at least two participants are symmetric. The technique of the derivation of necessary and sufficient conditions for existence of symmetric core is demonstrated. It is proved that they can be used for proof of core emptiness.
Keywords: cooperative TU game, symmetric players, symmetric core, existence condition.
Кооперативная игра с трансферабельными полезностями (N ,ν ) , где N = {1,..., n} - множество игроков, ν : 2N → R - характеристическая функция, является простой и популярной моделью экономических ситуаций, участники которых, объединяя свои ресурсы, капиталы, возможности могут получить дополнительную прибыль. О приложениях таких игр говорят уже их названия: рыночные игры (market games); картель-игры (cartel formation games); игры коллективного страхования (insurance games); холдинговые игры (holding games); инфраструктурные игры (infrastructure cost games); патентные игры (patent licensing games); инвестиционные игры (investment games); производственные игры (production games); игры банкротства (bankruptcy games) и многие другие. Конфликт (хотя и не антагонистический) состоит в том, что каждый агент стремится максимизировать свою долю совместного дохода. Игровая модель решает две взаимосвязанные проблемы: помогает выбрать партнеров и «справедливо» распределить прибыль. Будем предполагать, что игра (N ,ν ) неотрицательна и наиболее выгодно объединение всех участников (образование коалиции N ).
Игроков, вклады которых в любую коалицию S∈ 2N \ {Ø} одинаковы, называют симметричными. Игра симметрична, если симметричны все ее участники. Симметричными являются агенты, имеющие в моделируемой ситуации равные возможности. Но обратное не верно. Кроме того, несимметричные игроки могут стать симметричными после 0-нормализации игры. Рассмотрим в качестве примера ситуацию с четырьмя инвесторами (стартовые капиталы: 40, 30, 25, 25) и тремя инвестиционными проектами: 10% банковский депозит; инвестирование, дающее 15% прибыли (вклад должен быть кратным 50 д.е.); инвестирование, дающее 20% прибыли (вклад должен быть кратным 100 д.е.). В соответствующей кооперативной игре [1] (N ,ν ) , где
симметричны только игроки 3 и 4. 0-нормализация игры предполагает, что каждый агент уже получил сумму, которую может иметь без кооперации. В новой игре ( N,ν′) , где
ν′(i) = 0, i ∈ N , ν′(N ) = 10 , ν′(S) = 2.5, |S|∈ {2,3}, (2)
распределяется остаток кооперативной прибыли 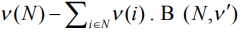 симметричны все игроки.
симметричны все игроки.
Присутствие симметричных игроков влияет на выбор концепции решения игры. Выигрыши симметричных игроков должны совпадать, т.е. нужно решение, удовлетворяющее аксиоме симметричности. Однако С-ядро (core)
(самое распространенное решение) этим свойством не обладает. Например, С-ядро игры (2), несмотря на ее симметричность, содержит дележ (1.25, 1.25, 1.25, 6.25) , согласно которому один из симметричных игроков получает больше половины дополнительного дохода от кооперации. Для исключения таких дележей в [2] введено понятие симметричного ядра (symmetric core)
Csym(ν ) = {x∈ C(ν )|xi = xj для симметричных игроков i, j∈ N}.
Ясно, что симметричное ядро симметричной игры, если оно существует, состоит из единственного дележа (ν (N ) / n,...,ν ( N ) / n) ∈ Rn . Для игры (2) это дележ (2.5, 2.5, 2.5, 2.5) , которому соответствует вектор выигрышей (46.5, 35.5, 30, 30) агентов в исходной игре (1).
Симметричное ядро мало исследовано. Цель данной заметки - продемонстрировать технику получения необходимых и достаточных условий существования Csym (ν ) , аналогичную выводу критерия непустоты С-ядра [3], использующего пару двойственных задач линейного программирования
С-ядро игры (N ,ν ) не пусто тогда и только тогда, когда
где ext M n - семейство крайних точек допустимого множества M n задачи (4). Чтобы описать класс игр, имеющих симметричное ядро, задачу (3) нужно преобразовать. С-ядро и симметричное ядро инвариантны относительно стратегической эквивалентности, поэтому без ограничения общности можно рассматривать игру в 0-форме. В таблице 1 приведен явный вид (3) и новых задач для 0-нормализованной игры 4 лиц с двумя и тремя симметричными игроками.
Таблица 1 – ЛП-задачи для игры четырех лиц
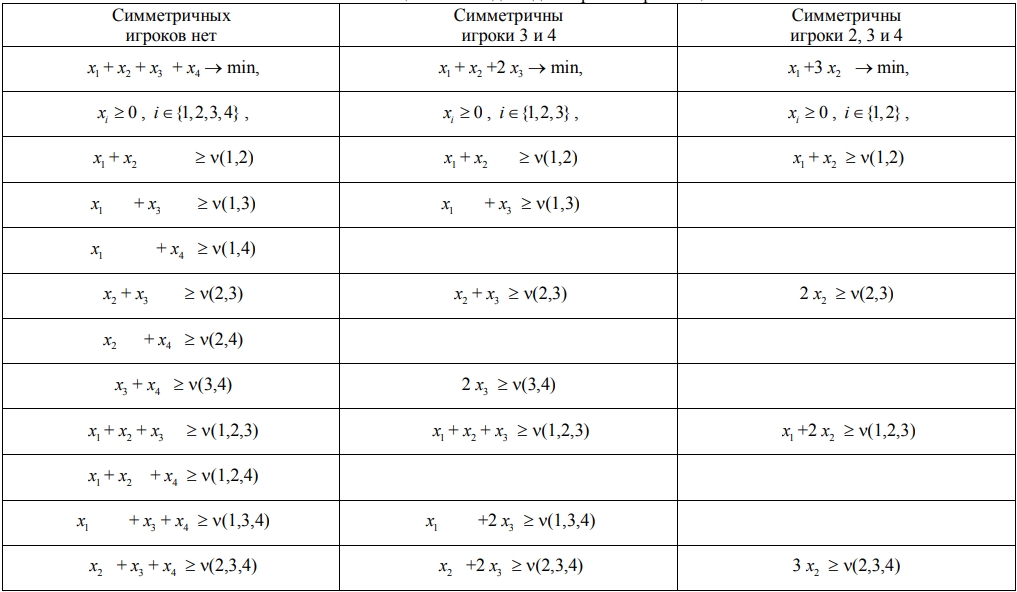 Количество крайних точек допустимых областей двойственных задач уменьшается при увеличении числа симметричных
Количество крайних точек допустимых областей двойственных задач уменьшается при увеличении числа симметричных 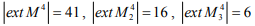 (нижний индекс - число симметричных агентов).
(нижний индекс - число симметричных агентов).
Описанный подход был использован для вывода критерия существования симметричного ядра игры n лиц с (n - 1) симметричными агентами [4]. В частности, необходимое и достаточное условие существования симметричного ядра в игре 4 лиц с тремя симметричными агентами имеет вид:
3ν (2,3) £ 2ν (N ), 3ν (1, 2) + 2ν (2, 3, 4) ≤ 3ν (N ), ν (1, 2) +ν (2,3) ≤ ν (N ), ν (2,3, 4) ≤ ν ( N ), ν (2,3) + 2ν (1, 2, 3) ≤ 2ν (N ), 3ν (1, 2,3) +ν (2,3, 4) ≤ 3ν (N ).
Критерий существования симметричного ядра содержит меньше неравенств, чем (5), поэтому практическое значение имеет доказательство того, что C(ν )≠Ø тогда и только тогда, когда Csym (ν )≠Ø . По определению Csym (ν) ⊆ C(ν ) , значит из Csym (ν)≠Ø следует C(ν)≠Ø. Пусть C(ν )≠Ø и x1 Î C(ν ) . Если x1 ∈ Csym(ν ) , то Csym(ν )≠Ø. В противном случае, xi1≠xj1 для некоторой пары i, j симметричных игроков. Так как С-ядру принадлежит также дележ x2 , где x2 = x1 , x2 = x1 , x2 = x1 для всех l∈ N \ {i, j} и C(ν ) - выпукло, то 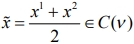 . Получили дележ
. Получили дележ 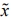 , в котором
, в котором 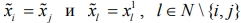 . Повторяя описанное преобразование для нового дележа мы (за конечное число шагов) получим элемент симметричного ядра.
. Повторяя описанное преобразование для нового дележа мы (за конечное число шагов) получим элемент симметричного ядра.
Использование симметричного ядра в качестве концепции решения игры, содержащей симметричных агентов, не исключает парадоксы. Существуют имеющие приложения игры, в которых единственный дележ С-ядра, а, следовательно, и симметричного ядра, не согласуется с моделируемой ситуацией [5, 6]. В работе [6] показано, что для таких игр подходят одноэлементные решения (значения игры), удовлетворяющие аксиоме симметричности, но не являющиеся селекторами С-ядра. Например, значение Шепли или консенсус-значение.
Литература
- De Waegenaere , Suijs J., Tijs S. Stable profit sharing in cooperative investment // OR Spectrum. - 2005. - V. 27. - № 1. – P. 85-93.
- Norde , Fragnelli V., Garcia-Jurado I., Patrone F., Tijs S. Balancedness of infrastructure cost games // European Journal of Operational Research. - 2002. - V. 136. - P. 635-654.
- Shapley S. On balanced sets and cores // Naval Research Logistics Quarterly. - 1967. - V. 14. - P. 453-460.
- Zinchenko B. Balancedness of (n-1)-symmetric n-person cooperative TU games // Nauka I Studia. - 2012. - NR 11 (56). - P.5-12.
- Зинченко А.Б., Мироненко Г.В., Провоторова П.А. Консенсус-значение для игр с коалиционной структурой // Математическая теория игр и ее приложения. - 2010. –Т. 2. – В. 1. - С. 93-106.
- Zinchenko B. On polytope of (0-1)-normal big boss games: redundancy and extreme points // Contributions to game theory and management. Collected papers of the Fifth International Conference «Game Theory and Management». SPbU. - 2012. - V. 5. - P. 386-397.