КОЭФФИЦИЕНТ ПУАССОНА ДЕНТИНА КАК АНИЗОТРОПНОЙ СРЕДЫ С ГЕКСАГОНАЛЬНОЙ СИММЕТРИЕЙ
КОЭФФИЦИЕНТ ПУАССОНА ДЕНТИНА КАК АНИЗОТРОПНОЙ СРЕДЫ С ГЕКСАГОНАЛЬНОЙ СИММЕТРИЕЙ
Научная статья
Муслов С.А.1, *, Лисовенко Д.С.2
1 Московский государственный медико-стоматологический университет им. А.И. Евдокимова, Москва, Россия;
2 Институт проблем механики им. А.Ю. Ишлинского РАН, Москва, Россия
* Корреспондирующий автор (muslov[at]mail.ru)
АннотацияКоэффициент Пуассона (поперечной деформации) играет важную роль в деформационном поведении материалов. Наравне с модулем Юнга он составляет двойку независимых и наиболее информативных материальных констант твердых тел. Для твердых тканей зуба (эмали и дентина) коэффициент Пуассона должен соответствовать коэффициенту Пуассона реставрационных материалов во избежание перенапряжений на границе разделов реставрационный материал-эмаль и реставрационный материал-дентин. Кроме того, величина коэффициента Пуассона влияет на деформационную прочность эмали и дентина, а именно трещиностойкость, при возникновении в них напряженно-деформированного состояния. В данной работе впервые получена ориентационная зависимость коэффициента Пуассона дентина зубов на основе матриц упругих постоянных и коэффициентов податливости гексагональных кристаллов, какими являются кристаллы гидроксиапатита дентина. Результаты вычисления коэффициентов Пуассона дентина как кристаллической системы с гексагональной структурой представлены в виде таблиц и на диаграммах в полярной и декартовой системах координат. Также рассчитаны минимальный и максимальный коэффициенты для соответствующих направлений продольной и поперечной деформаций в кристаллографической системе координат. Показано, что максимальное значение коэффициента Пуассона дентина (0,53) больше верхнего предела для коэффициента Пуассона изотропных материалов, в том числе известных реставрационных материалов, что в ряде случаев может снижать качество реставраций в микрообъемах. Отмечается, что аналогичный анализ может быть выполнен и для эмали зубов.
Ключевые слова: дентин, коэффициент Пуассона, упругая анизотропия.
POISSON'S RATIO OF DENTIN AS ANISOTROPIC MEDIUM WITH HETEROGONAL SYMMETRY
Research article
Muslov S.A.1, *, Lisovenko D.S.2
1 Moscow State University of Medicine and Dentistry named after A.I. Evdokimov, Moscow, Russia;
2 Ishlinsky Institute for Problems in Mechanics of the RAS, Moscow, Russia
* Corresponding author (muslov[at]mail.ru)
AbstractThe Poisson's ratio (transverse deformation) plays an important role in the deformation behavior of materials. Along with the Young's module, it constitutes a pair of independent and most informative material constants of solids. For hard tissues of the tooth (enamel and dentin), the Poisson's ratio should correspond to the Poisson's ratio of restorative materials in order to avoid overvoltages at the boundary of the sections restorative material-enamel and restoration material-dentin. In addition, the value of the Poisson's ratio affects the deformation strength of enamel and dentin, namely, crack resistance, when they occur in a stressed-deformed state. In this paper, the orientational dependence of the Poisson's ratio of dentin teeth on the basis of matrices of elastic constants and the compliance coefficients of hexagonal crystals, such as crystals of dentine hydroxyapatite, was obtained for the first time. The results of calculating the Poisson's ratios of dentin as a crystalline system with a hexagonal structure are presented in the form of tables and diagrams in the polar and Cartesian coordinate systems. The minimum and maximum coefficients for the corresponding directions of the longitudinal and transverse deformations in the crystallographic coordinate system are also calculated. It is shown that the maximum value of the Poisson's ratio of dentin (0,53) is greater than the upper limit for the Poisson's ratio of isotropic materials, including known restoration materials, which in some cases may reduce the quality of restorations. It is noted that a similar analysis can be performed for tooth enamel.
Keywords: dentin, Poisson's ratio, elastic anisotropy.
Введение
Упругие свойства твердых тканей зуба и гидроксиапатита, как минеральной их составляющей, достаточно часто вызывают интерес у исследователей [8], [9]. Однако остаются актуальными и до конца неизученными ряд аспектов этой тематики, в частности величина коэффициента Пуассона поперечной деформации эмали и дентина как анизотропных сред с гексагональной симметрией. Этот вопрос особенно представляет интерес с позиций прочностных свойств тканей зуба, представляющих в контексте теории разрушения микронеоднородную среду со сложным характером напряженно-деформированного состояния в микрообъемах. Анизотропия и неоднородность твердых тканей зуба сред повышают степень концентрации микронапряжений, ответственных за возникновение микротрещин Гриффитса и пластических деформаций, в зависимости от степени анизотропии и неоднородности. В данном сообщении мы представляем достаточно подробное исследование величины коэффициента Пуассона дентина как анизотропной среды гексагональной сингонии – три элементарных ячейки образуют правильную призму на шестигранном основании. В связи с тем, что в литературе до сих пор не сложились единые обозначения и в связи с этим также расчетные формулы для определения упругих характеристик анизотропных сред наше исследование проведено на основании двух различных методик расчета [2], [12].
Расчеты и результаты
- Коэффициент Пуассона (коэффициент поперечной деформации) µ является весьма информативной характеристикой при анализе деформационного поведения твердых тел. Для реально упругих тел, увеличивающих свой объем при растяжении и уменьшающих при сжатии, величина µ может лежать только в пределах от 0 до 0,5 [1]. Практически для большинства материалов коэффициент Пуассона находится еще в более узком интервале: от 0,2 до 0,4 [3]. Однако по современным представлениям диапазон возможных значений коэффициента Пуассона существенно расширен за оба предела: может быть и отрицательным µ<0 (ауксетики), и больше 0,5. Известно, что коэффициент Пуассона характеризует отношение поперечной деформации к продольной и является одной из упругих констант материала.
Для дентина коэффициент по литературным данным лежит в интервале 0,29-0,33 [5]. По результатам ультразвуковых измерений [11] он равен 0,32. Считается, что дентин представляет собой биокомпозит и состоит приблизительно на 45-70 % из неорганического материала в форме кристаллов гидроксиапатита [6], [10]. Кристаллы гидроксиапатита расположены между коллагеновыми волокнами и по классу симметрии относятся к гексагональной сингонии. Поэтому есть все основания полагать рассматривать дентин как анизотропную среду, а это значит, что его упругие свойства описываются матрицей упругих постоянных cij или коэффициентов податливости sij. Коэффициенты Пуассона такой среды в генерализованной общей форме могут быть определены как ![]() , где εkl – компоненты тензора деформации. В результате гексагональные системы и дентин тоже описываются не одним, а двумя коэффициентами Пуассона
, где εkl – компоненты тензора деформации. В результате гексагональные системы и дентин тоже описываются не одним, а двумя коэффициентами Пуассона ![]() [12]. Штрихи показывают, что данные компоненты µ отнесены не к кристаллографической, а к специальной (лабораторной) системе координат, связанной с зубом с помощью углов Эйлера и отличной, вообще говоря, от кристаллографической. По литературным данным значения упругих постоянных дентина достаточно хорошо известны, поэтому зная их, можно вычислить коэффициенты податливости и Пуассона дентина по формулам [4], [12] для гексагональных кристаллов:
[12]. Штрихи показывают, что данные компоненты µ отнесены не к кристаллографической, а к специальной (лабораторной) системе координат, связанной с зубом с помощью углов Эйлера и отличной, вообще говоря, от кристаллографической. По литературным данным значения упругих постоянных дентина достаточно хорошо известны, поэтому зная их, можно вычислить коэффициенты податливости и Пуассона дентина по формулам [4], [12] для гексагональных кристаллов:
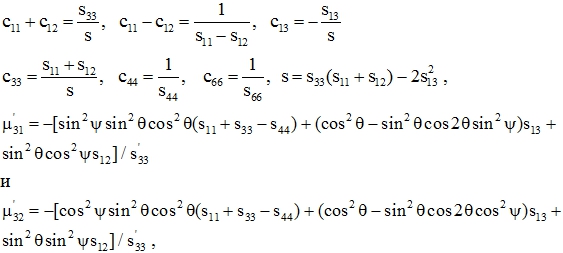
где ![]() , θ и Ψ – углы Эйлера (описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве).
, θ и Ψ – углы Эйлера (описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве).
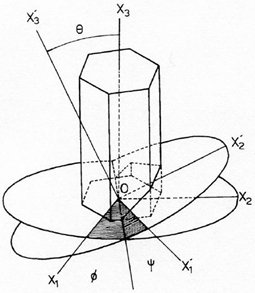
Рис. 1 – Гексагональная ячейка и ортогональная система координат xi, где Оx3 совпадает с направлением <c> оси кристалла. Вращение ортогональной системы Xi относительно системы xi описывается в терминах трёх углов Эйлера θ, ϕ и ψ
Значения упругих постоянных cij и коэффициентов податливостей дентина Sij представлены в табл. 1 и 2.
Таблица 1 – Упругие постоянные (ГПа) дентина
| с11 | с12 | с13 | с33 | с44 |
| 37,00 | 16,60 | 8,70 | 39,00 | 5,70 |
Таблица 2 – Коэффициенты податливости (ГПа-1) дентина
| s11 | s12 | s13 | s33 | s44 |
| 0,0346 | -0,0145 | -0,0045 | 0,0276 | 0,1754 |
Результаты вычисления коэффициентов Пуассона дентина как кристаллической системы с гексагональной структурой представлены на рис. 2 (в полярных координатах) и рис. 3 (в декартовых координатах). Вследствие симметрии и для простоты изложения графики приведены только для ![]() .
.
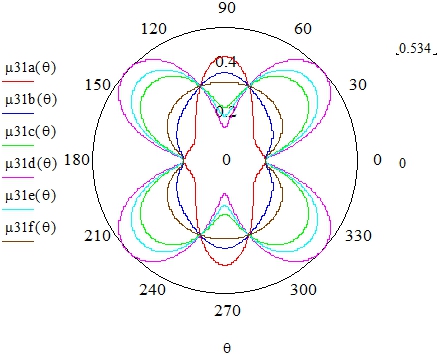
Рис. 2 – Полярные координаты. Коэффициент Пуассона дентина ![]() для различных направлений θ и Ψ.
для различных направлений θ и Ψ. ![]() радиан, соответственно. 1 радиан=57°
радиан, соответственно. 1 радиан=57°
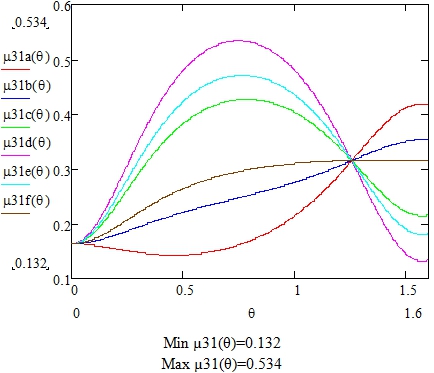
Рис. 3 – Декартовы координаты. Коэффициент Пуассона дентина ![]() для различных направлений θ и Ψ.
для различных направлений θ и Ψ. ![]() радиан, соответственно
радиан, соответственно
Из рисунков отчетливо следует выраженное анизотропное поведение коэффициента Пуассона кристаллов дентина. Его значения в зависимости от направления в пространстве изменяются в весьма широких пределах (в 4 с лишним раза).
Отметим аномально высокую величину максимального значения коэффициента Пуассона (0,534) вдоль ряда направлений, что крайне необычно для изотропных материалов. Это означает, что при сжатии локальных областей дентина вдоль этих направлений их объем будет увеличиваться, а при растяжении – наоборот, уменьшаться. Упругое поведение под нагрузкой реставрационного материала принципиально другое (μ пломбировочного материала существенно меньше 0,5), поэтому при сжатии его объем уменьшается, а при растяжении – увеличивается. Это несоответствие в деформационном поведении на границе разнородных сред пломбировочного материала и дентина может привести к образованию доменов перенапряжений на данной границе, ослаблению сцепления реставрационного материала с дентином и, как негативный итог, деградации фиксации и часто встречаемой ситуации разрушения прямой, а порой и непрямой реставрации, особенно композиционными материалами.
Кроме того, известно, что величина коэффициента Пуассона тесно связана и прямо влияет на деформационную прочность кристаллов, а именно на трещиностойкость. Как известно, очагами разрушения материалов служат небольшие зародышевые микротрещины различного происхождения. Считается, что микротрещины в момент зарождения имеют длину ~ 10-6-10-4 мм. Распространение трещин может привести к разрушению зуба, то есть разделению его на части. Разрушение носит хрупкий характер и происходит, как правило, при малых деформациях, без заметных пластических. В теории Гриффитса для объемного напряженного состояния показано, что величина критического напряжения σ, начиная с которого хрупкая трещина стартует и начинает неограниченно расти зависит от значения µ [5]. Это следует из нижеприведенной формулы и графика на рис. 4:
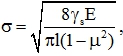
где γs – удельная поверхностная энергия дентина, Е – модуль Юнга, l – длина микротрещины. Из рисунка видно, что чем выше коэффициент Пуассона, тем сильнее критическое напряжение зависит от него. С учетом того, что максимальные напряжения действуют в периферийной части ткани зуба вероятность старта трещины там также максимальна. В средней части зуба, где располагается пульпа, внутренние силы минимальны, соответственно вероятность старта будет меньше. Мы можем сделать некоторые оценки. Если положить ![]() и l=10-6 м=1 мкм, то получим при µ=0,13 σ=2,64 ГПа, а при µ=0,52 σ=3,12 ГПа. Далее, если гипотетически предположить, что данные напряжения приложены к площади 1 мм2=10-6 м2, то сила, вызвавшая это напряжение будет равна в первом случае 2,64 кН, во втором – 3,12 кН. Напомним, что жевательная мышца по данным [13] развивает усилия до 1 кН (например при раскалывании ореха, косточек слив или абрикосов).
и l=10-6 м=1 мкм, то получим при µ=0,13 σ=2,64 ГПа, а при µ=0,52 σ=3,12 ГПа. Далее, если гипотетически предположить, что данные напряжения приложены к площади 1 мм2=10-6 м2, то сила, вызвавшая это напряжение будет равна в первом случае 2,64 кН, во втором – 3,12 кН. Напомним, что жевательная мышца по данным [13] развивает усилия до 1 кН (например при раскалывании ореха, косточек слив или абрикосов).
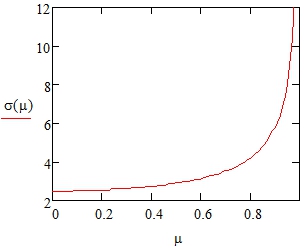
Рис. 4 – Зависимость напряжения старта трещины (ГПа) от коэффициента Пуассона для объемного напряженного состояния дентина, ![]() , [5] и l=10-6 м=1 мкм
, [5] и l=10-6 м=1 мкм
2. Заслуживает внимания подход, основанный на расчете экстремальных значений коэффициента Пуассона кристаллических сред и построения изоповерхностей коэффициента в пространстве. Зная упругие постоянные, можно вычислить коэффициенты податливости и “технические” упругие характеристики (модуль Юнга, коэффициент Пуассона и модуль Юнга) дентина по формулам для гексагональной сингонии с использованием связи между коэффициентами податливости и жесткости. Модуль Юнга E, коэффициент Пуассона V и модуль сдвига G для гексагональных кристаллов можно записать в виде [2], [7]:
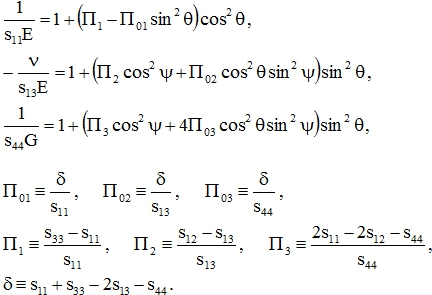
Результаты вычисления коэффициентов Пуассона дентина как кристаллической гексагональной структуры представлены в табл. 3 и на рис. 6.
В табл. 3 последние четыре цифры в квадратных скобках указывают направление растяжения, а первых четыре – направление поперечной деформации. Четырехиндексовая система Миллера-Браве используется для определения направлений в гексагональной решетке (рис. 5). В гексагональной решетке начало координат помещают в центр основания элементарной ячейки. Кристаллографические оси х и у проходят из этого центра через вершины шестиугольного основания элементарной ячейки, располагаясь под углом 120° одна к другой, а ось z является вертикальной осью гексагональной призмы. За единицу измерения вдоль осей х и у принимают период решетки а, а вдоль оси z – период с.
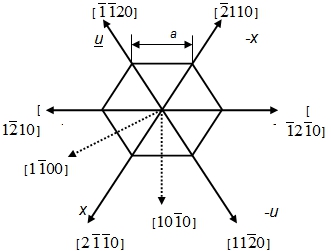
Рис. 5 – Примеры кристаллографических направлений в гексагональной решетке (базисная плоскость, ось z перпендикулярна плоскости чертежа)
В плоскости базиса проводят дополнительную ось u, расположенную под углом 120° к осям х и у. Направление -u находится между направлениями +x и +y. Дополнительный индекс i определяют точно так же, как и индексы Миллера, и ставят на третьем месте [hkil].
Таблица 3 – Экстремальные значения коэффициента Пуассона (![]() ) для дентина, а также значения коэффициентов Пуассона в частных ориентациях (см. рис. 5)
) для дентина, а также значения коэффициентов Пуассона в частных ориентациях (см. рис. 5)

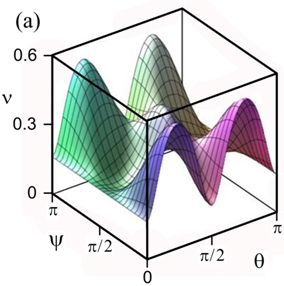
Рис. 6 – Изменчивость коэффициента Пуассона ν дентина в пространстве
На рис. 6. представлена поверхность коэффициента Пуассона для дентина. Из него отчетливо следует выраженный анизотропный характер коэффициента Пуассона. Его значения в зависимости от направления (углов Эйлера θ и ψ) изменяются в широких пределах (до четырех с лишним раз или на 6,18 децибел).
Отметим также аномально высокую величину максимального значения коэффициента Пуассона (0,54) вдоль ряда направлений, что оказывается выше значения верхнего предела для коэффициента Пуассона изотропных материалов. Кроме того, максимальное и минимальное значения коэффициента Пуассона хорошо согласуются с данными, полученными с помощью первого подхода для расчета коэффициента Пуассона как анизотропной среды (см. рис. 1, 2).
В заключении отметим, что аналогичный анализ может быть выполнен и для эмали зубов, состоящей из неорганических минералов, в основном кристаллов апатитов с гексагональной структурой, на 90-97% [6, 10].
Выводы
- Дентин зубов не является изотропной средой вследствие симметрии его минеральной составляющей (кристаллов гидроксиапатита).
- Установлена выраженная анизотропия коэффициента Пуассона дентина на основе расчетов по формулам упругих постоянных и коэффициентов податливости для гексагональной сингонии. Максимальное значение коэффициента Пуассона (0,53-0,54) более чем в 4 раза превышает минимальное (0,13).
- Максимальное значение коэффициента Пуассона оказывается выше значения верхнего предела для коэффициента Пуассона изотропных, в том числе реставрационных материалов, используемых в стоматологии, что может сказываться на качестве реставраций. В данном контексте высказано предположение, что установленная упругая анизотропия дентина с кристаллической гексагональной симметрией является клинически нежелательным фактором.
- Более тщательный анализ упругой анизотропии дентина как минерально-органического комплекса и микронеоднородной гетерофазной системы возможен с привлечением достижений теории анизотропных сред с кристаллографической текстурой (несмотря на то, что все призмы минеральных веществ в дентине обладают одинаковым или схожим кристаллическим строением, они отличаются взаимной ориентацией кристаллографических осей). Дальнейший анализ быть основан на знании характера пространственного распределения кристаллографических осей отдельных минеральных призм дентина.
- Изучение показателей анизотропии дентина как анизотропной неоднородной среды приобретает практическое значение при изучении проблем прочности тканей зуба и качества реставраций.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Беломестных В.Н. Коэффициент Пуассона и параметр Грюнайзена твердых тел / Беломестных В.Н., ТеслеваЕ.П. // Известия Томского политехнического университета. – 2003. – Т. 306. – № 5. – С. 8-12.
- Гольдштейн Р.В. Изменчивость упругих свойств гексагональных ауксетиков / Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. // ДАН – 2011. – Т. 441 – № 4 – C. 468-471.
- Иванов Г.П. О физическом смысле коэффициента Пуассона / Иванов Г.П., Лебедев Т.А. // Труды Ленингр. политехн. ин-та им. М.И. Калинина. – 1964. – № 236. – С. 38-46.
- Най Д. Физические свойства кристаллов. М.: ИЛ, 1960. – 385 с.
- Перцов C.C. Основы биомеханики для стоматологов / С.С. Перцов, Г.М. Стюрева, С.А. Муслов и др. // МГМСУ, 2017. – 115 с.
- Хышиктуев Б.С. Биохимия полости рта: Учебное пособие / Хышиктуев Б.С., Хышиктуева Н.А. // Чита: ИИЦ ЧГМА, 2004 – 84 с.
- Goldstein R.V. Extreme values of the shear modulus for hexagonal crystals. Scripta Mater / R.V. Goldstein, V.A. Gorodtsov, M.A. Komarova and others // doi: 10.1016/j.scriptamat.2017.07.002.
- Katz J.L. On the anisotropic elastic properties of hydroxyapatite / J.L. Katz, K. Ukraincik // Journal of Biomechanics – V 4. – Issue 3. – 1971. – P 221-227. doi: 10.1016/0021-9290(71)90007-8.
- Katz J.L. Hard tissue as a composite material-I. Bounds on the elastic behavior / .L. Katz. J. // Journal of Biomechanics – V 4. – Issue 5. – 1971. – P 455-473. doi: 10.1016/0021-9290(71)90064-9.
- Lees S. The role of collagen in the elastic properties of calcified tissues / Lees S, Davidson C.L. //. Journal of Biomechanics – 1977. – 10(8) – P. 473-86.
- Lees S. Anisotropy in hard dental tissues. J. Biomech. 1972 5 6 557-64.
- Povolo F. Poisson's ratio in zirconium single crystals. J. of Nuclear Materials, Volume 118, Issue 1, August 1983, Pages 78-82.
- Prium G.J. Forces acting on the mandible during bilateral static bite at different bite force levels / Prium G.J., De Jongh H.J., Ten Bosch J.J. // J Biomech, 13: 735-763, 1980.
Список литературы на английском языке / References in English
- Belomestnykh V.N. Koeffitsiyent Puassona i parametr Gryunayzena tverdykh tel [Poisson's Ratio and Gruneisen Parameter of Solids] / Belomestnykh V.N., TeslevaP. // Izvestiya Tomskogo Polytechnicheskogo Universita [Bulletin of the Tomsk Technical Univarsity] - 2003. – V. 306. – NO. 5. – P. 8-12. [in Russian]
- Goldstein R.V. Izmenchivost' uprugikh svoystv geksagonal'nykh auksetikov. DAN [Variability of Elastic Properties of Hexagonal Auxetics. DAN] / Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. // 2011, V. 441, No. 4, p. 468-471. [in Russian]
- Ivanov G.P. O fizicheskom smysle koeffitsiyenta Puassona [On Physical Meaning of Poisson's Ratio] / Ivanov G.P., Lebedev T.A. // Trudy Leningradskogo. Polytechnicheskogo Instituta im. M.I. Kalinina [Works of the Leningrad Technical Institute named after M.I. Kalinin]. – 1964. – No. 236. – P. 38-46. [in Russian]
- Nai D. Fizicheskiye svoystva kristallov [Physical Properties of Crystals]. Moscow: IL, 1960. 385 p. [in Russian]
- Pertsov S.S. Osnovy biomekhaniki dlya stomatologov. [Fundamentals of Biomechanics for Dentists] / S.S. Pertsov, G.M. Styureva, S.A. Muslov and others // MGMSU, 2017. - 115 p. [in Russian]
- Khyshiktuev B.S. Biokhimiya polosti rta: Uchebnoye posobiye [Biochemistry of Oral Cavity: Textbook.] / Khyshiktuev B.S., Khyshiktueva N.A. – Chita: Information and Analytical Center of ChSMA, 2004. – 84 p. [in Russian]
- Goldstein R.V. Extreme values of the shear modulus for hexagonal crystals. Scripta Mater / R.V. Goldstein, V.A. Gorodtsov, M.A. Komarova and ohers // doi: 10.1016/j.scriptamat.2017.07.002.
- Katz J.L. On the anisotropic elastic properties of hydroxyapatite / J.L. Katz, K. Ukraincik // Journal of Biomechanics – V 4. – Issue 3. – 1971. – P 221-227. doi: 10.1016/0021-9290(71)90007-8.
- Katz J.L. Hard tissue as a composite material—I. Bounds on the elastic behavior / .L. Katz. J. // Journal of Biomechanics – V 4. – Issue 5. – 1971. – P 455-473. doi: 10.1016/0021-9290(71)90064-9.
- Lees S. The role of collagen in the elastic properties of calcified tissues / Lees S, Davidson C.L. //. Journal of Biomechanics – 1977. – 10(8) – P. 473-86.
- Lees S. Anisotropy in hard dental tissues. J. Biomech. 1972 5 6 557-64.
- Povolo F. Poisson's ratio in zirconium single crystals. J. of Nuclear Materials, Volume 118, Issue 1, August 1983, Pages 78-82.
- Prium G.J. Forces acting on the mandible during bilateral static bite at different bite force levels / Prium G.J., De Jongh H.J., Ten Bosch J.J. // J Biomech, 13: 735-763, 1980.
