КЛАССИФИКАЦИЯ ОБОБЩЕННЫХ УРАВНЕНИЙ БЕТХЕРА ВТОРОГО ПОРЯДКА
КЛАССИФИКАЦИЯ ОБОБЩЕННЫХ УРАВНЕНИЙ БЕТХЕРА ВТОРОГО ПОРЯДКА
Научная статья
Кальницкий В.С.1, *, Петров А.Н.2
1 ORCID: 0000-0002-3937-6078;
2 ORCID: 0000-0001-6853-5480;
1 Санкт-Петербургский государственный университет, Санкт-Петербург, Россия;
2 Военная академия материально-технического обеспечения имени генерала армии А. В. Хрулёва, Санкт-Петербург, Россия
* Корреспондирующий автор (st006987[at]spbu.ru)
АннотацияВ статье подводится итог исследований авторов о решении обобщенных уравнений Бетхера второго порядка от двух аргументов. Целью исследования является описание класса гладких решений таких уравнений, определённых на некоторой конической области с вершиной в начале координат. Решающим оказался метод прямого описания орбит действия общей линейной группы на пространстве тензоров типа (2,1), симметричных по ковариантным индексам. В статье были доказаны структурные теоремы о строении орбит (теоремы 1-4). Было доказано, что любое обобщённое уравнение Бетхера второго порядка приводит к одному из тринадцати типов уравнений, соответствующих тензорам, названных авторами каноническими (теорема 5). В данном исследовании часть обобщённых уравнений Бетхера решена полностью, и остальная часть сведена к четырём однопараметрическим и двум двухпараметрическим семействам функциональных уравнений Шрёдера от одной переменной. Приведены частичные решения указанных уравнений.
Ключевые слова: уравнение Бетхера, уравнение Шрёдера, функциональное уравнение, эндоморфизм Фробениуса.
A CLASSIFICATION OF GENERALIZED SECOND-ORDER BÖTTCHER'S EQUATIONS
Research article
Kalnitsky V.S.1, *, Petrov A.N.2
1 ORCID: 0000-0002-3937-6078;
2 ORCID: 0000-0001-6853-5480;
1 Saint Petersburg State University, Saint Petersburg, Russia;
2 Military Educational Institution of Logistics named after General of the Army A.V. Кhrulyov, Saint Petersburg, Russia
* Corresponding author (st006987[at]spbu.ru)
AbstractThe authors of the article summarize their research on the solution of generalized Böttcher's equation of the second order from two arguments. The aim of the study is to describe a class of smooth solutions of these equations defined on a certain conic domain with a vertex at the origin. The method of direct description of the orbits of the action of a general linear group on the space of tensors of type (2,1), which are symmetric with respect to covariant indices, proved to be resolving. In the article, structural theorems on the structure of orbits were proved (Theorems 1-4). It was also proved that any generalized second-order Böttcher's equation belongs to one of the thirteen types of equations corresponding to tensors, which were called canonical by the authors (Theorem 5). In this article, part of the generalized Böttcher's equation is solved completely and the rest is reduced to four one-parameter and two two-parameter families of the functional Schröder's equations from one variable. The study also presents partial solutions to these equations.
Keywords: Böttcher's equation, Schröder's equation, functional equation, Frobenius endomorphism.
Основные определения и обозначенияОпределение 1 ([1]). A – 2-мерная коммутативная ![]() –алгебра. Отображения
–алгебра. Отображения ![]() называются эндоморфизмами Фробениуса.
называются эндоморфизмами Фробениуса.
Определение 2. Отображение ![]() для которого выполняется соотношение
для которого выполняется соотношение ![]() называется сплетающим отображением, эндоморфизм Δ2 называется 2-мерным представлением эндоморфизма δ2 в алгебре A. Если отображение φ определено на некоторой открытой в стандартной топологии области
называется сплетающим отображением, эндоморфизм Δ2 называется 2-мерным представлением эндоморфизма δ2 в алгебре A. Если отображение φ определено на некоторой открытой в стандартной топологии области ![]() то будем говорить о локальном представлении.
то будем говорить о локальном представлении.
Зафиксируем базис ![]() 2-мерной алгебры и запишем структурные константы
2-мерной алгебры и запишем структурные константы
![]() (1)
(1)
здесь и далее мы будем придерживаться соглашения Эйнштейна о суммировании. Пусть ![]() является сплетающим отображением
является сплетающим отображением ![]() Разложим произвольный элемент алгебры по выбранному базису
Разложим произвольный элемент алгебры по выбранному базису ![]() и определим функцию
и определим функцию ![]() Выполнено следующее соотношение
Выполнено следующее соотношение
Таким образом, сплетающее отображение является решением уравнения (2), которое называется обобщённым уравнением Бетхера порядка 2 [2, C. 375].
Рассмотрим задачу поиска неизвестной функции F для фиксированных коэффициентов ![]() Если решение F уравнения (2) найдено, то полагая
Если решение F уравнения (2) найдено, то полагая ![]() мы получим (локальное) сплетающее отображение для δ2 и Δ2.
мы получим (локальное) сплетающее отображение для δ2 и Δ2.
Пространство всех двухмерных коммутативных ![]() –алгебр с выбранным базисом отождествляется с пространством
–алгебр с выбранным базисом отождествляется с пространством ![]() тензоров типа (2,1), симметричных по ковариантным индексам. Действие группы
тензоров типа (2,1), симметричных по ковариантным индексам. Действие группы ![]() на пространстве
на пространстве ![]() задается формулами (3). Две алгебры, принадлежащие одной орбите действия группы
задается формулами (3). Две алгебры, принадлежащие одной орбите действия группы ![]() являются изоморфными и наоборот.
являются изоморфными и наоборот.
Определение 3. Тензор ![]() назовем каноническими, если
назовем каноническими, если ![]()
Теорема 1. В каждой орбите действия группы ![]() на пространстве
на пространстве ![]() существует канонический тензор.
существует канонический тензор.
Доказательство. Пусть ![]() – произвольный тензор. Запишем явно формулы преобразований коэффициентов тензора при повороте на угол t, т.е. действие матрицы
– произвольный тензор. Запишем явно формулы преобразований коэффициентов тензора при повороте на угол t, т.е. действие матрицы ![]()
![]()
Обозначим ![]() Согласно (3)
Согласно (3)
![]()
Если ![]() то рассмотрим два возможных случая:
то рассмотрим два возможных случая:
а) ![]() Чтобы добиться равенства
Чтобы добиться равенства ![]() достаточно взять
достаточно взять ![]()
б) ![]() В силу того, что свободный коэффициент
В силу того, что свободный коэффициент ![]() и старший коэффициент
и старший коэффициент ![]() многочлена третьей степени не равны нулю, он имеет вещественный корень
многочлена третьей степени не равны нулю, он имеет вещественный корень ![]() . Значит, определено
. Значит, определено ![]() такое, что действие матрицы приводит к выполнению равенства
такое, что действие матрицы приводит к выполнению равенства ![]() .
.
Следствие. В каждой орбите действия группы ![]() на пространстве
на пространстве ![]() существует канонический тензор.
существует канонический тензор.
Будем записывать группы структурных констант с верхним индексом 1 и 2 как коэффициенты двух квадратичных форм
![]()
которые мы будем называть вырожденными.
Теорема 2. Если тензор T не является вырожденным, то в его ![]() -орбите содержится не более трёх канонических тензоров.
-орбите содержится не более трёх канонических тензоров. 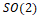 -орбита вырожденного тензора состоит из вырожденных тензоров.
-орбита вырожденного тензора состоит из вырожденных тензоров.
Доказательство. В силу теоремы 1 в 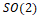 -орбите тензора T содержится канонический тензор T0. Рассмотрим
-орбите тензора T содержится канонический тензор T0. Рассмотрим 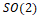 -орбиту тензора T0. Формула преобразования коэффициента
-орбиту тензора T0. Формула преобразования коэффициента ![]() примет вид
примет вид
![]()
Если ![]() то кубический многочлен имеет не более трёх корней, из которых один
то кубический многочлен имеет не более трёх корней, из которых один ![]() Если то при условии, что хотя бы один из двух коэффициентов квадратного трёхчлена не равен нулю, он имеет не более двух корней, из которых один и ещё один канонический тензор соответствует
Если то при условии, что хотя бы один из двух коэффициентов квадратного трёхчлена не равен нулю, он имеет не более двух корней, из которых один и ещё один канонический тензор соответствует ![]() В случае полного вырождения
В случае полного вырождения
![]()
вся орбита состоит из канонических тензоров, являющихся вырожденными.
Рассмотрим LQ-разложение ([3]) произвольной невырожденной матрицы ![]() – невырожденная нижнетреугольная матрица,
– невырожденная нижнетреугольная матрица, ![]() .
.
Теорема 3. L(2)-орбита канонического тензора T0 состоит из канонических тензоров.
Доказательство. Рассмотрим нижнетреугольную матрицу и обратную к ней
![]()
Согласно (3)
![]()
Теорема 4. Группа ![]() действует на множестве
действует на множестве ![]() , где O – тождественно нулевой тензор, транзитивно.
, где O – тождественно нулевой тензор, транзитивно.
Доказательство. Так как мы рассматриваем ненулевой тензор, то либо ![]() При повороте на
При повороте на ![]() оба коэффициента, согласно (3), меняются по правилу
оба коэффициента, согласно (3), меняются по правилу
![]()
![]()
Таким образом, в орбите вырожденного тензора есть тензор с Рассмотрим этот тензор. Запишем явно все формулы (3) для действия нижнетреугольной матрицы на тензор
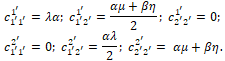
Полученный тензор имеет структуру вырожденного. Для доказательства транзитивности действия группы необходимо доказать, что любой ненулевой вырожденный тензор можно перевести в любой ненулевой вырожденный тензор. Рассмотрим два вырожденных тензора
![]()
если необходимо, применим поворот на ![]() чтобы оба первых коэффициента первых квадратичных форм были ненулевыми. Найдём коэффициенты нижнетреугольной матрицы, такие что выполняются соотношения
чтобы оба первых коэффициента первых квадратичных форм были ненулевыми. Найдём коэффициенты нижнетреугольной матрицы, такие что выполняются соотношения
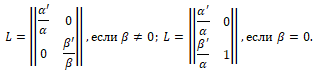
Следствие. Вырожденный ненулевой тензор всегда может быть приведён к виду ![]()
Определение 4. L(2) -орбиту канонического тензора будем называть канонической поверхностью.
Теорема 4 означает, что множество ![]() является 2-мерной
является 2-мерной ![]() -орбитой и канонической поверхностью одновременно. Теорема 3 означает, что в каждой
-орбитой и канонической поверхностью одновременно. Теорема 3 означает, что в каждой ![]() -орбите невырожденного тензора содержится не более трёх канонических поверхностей, являющихся не более чем 3-мерными L(2)-орбитами канонических тензоров.
-орбите невырожденного тензора содержится не более трёх канонических поверхностей, являющихся не более чем 3-мерными L(2)-орбитами канонических тензоров.
Классификационная теорема
Определение 5. Обобщённое уравнение Бетхера второго порядка, отвечающее каноническому тензору, будем называть каноническим уравнением.
Определение 6. Выбор одного канонического уравнения для каждой канонической поверхности будем называть классификацией обобщённых уравнений Бетхера второго порядка.
Теорема 5. Существует 13 типов канонических уравнений Бетхера, к которым может быть сведено любое нетривиальное уравнение Бетхера второго порядка.
Доказательство. Перечисление канонических уравнений начнём с канонической поверхности вырожденных тензоров, нумерацию типов будем вести римскими цифрами. Согласно следствию теоремы 4 в этой орбите всегда можно выбрать тензор, соответствующий уравнению Бетхера следующего вида: тип I.
Далее, вновь рассмотрим нижнетреугольную матрицу и обратную к ней ![]()
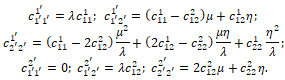
Из соотношений следует, что если у канонического тензора ![]() , то эти равенства сохраняются во всей L(2)-орбите. Таким образом, для классификации орбит следует рассмотреть три различных случая:
, то эти равенства сохраняются во всей L(2)-орбите. Таким образом, для классификации орбит следует рассмотреть три различных случая: ![]()
В случае II возникают три альтернативы:
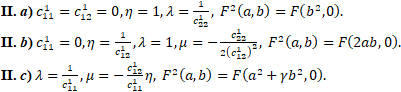
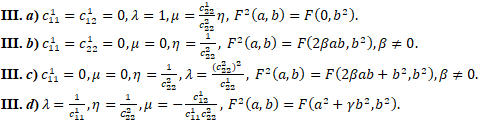 В случае IV возникают пять альтернатив:
В случае IV возникают пять альтернатив:
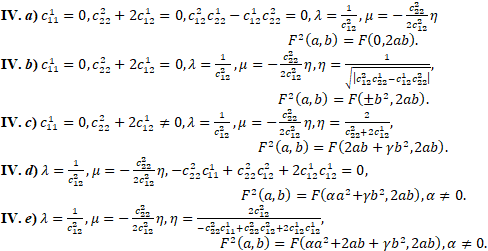
Мы получили 13 канонических уравнений Бетхера второго порядка. Любое уравнение может быть сведено к одному из перечисленных.
Решение канонических уравнений
Определение 7. Два дифференцируемых решения ![]() уравнения (2) такие, что на общей (не пустой) конической области определения с вершиной в начале системы координат, принимающие все положительные значения и при этом являющиеся функционально независимыми, называются базовыми решениями.
уравнения (2) такие, что на общей (не пустой) конической области определения с вершиной в начале системы координат, принимающие все положительные значения и при этом являющиеся функционально независимыми, называются базовыми решениями.
Теорема 6 ([1]). Если существуют два базовых решения, то общее решение обобщенного уравнения Бетхера имеет вид
![]()
I.![]()
Решение. Сразу запишем ![]() то есть на оси Ob функция F должна быть константой 1 или 0. Рассмотрим функцию
то есть на оси Ob функция F должна быть константой 1 или 0. Рассмотрим функцию![]()
![]()
Единственным гладким решением этого уравнения, определенном на луче, является функция ![]() – произвольная функция числового аргумента ξ (см. напр. [8]). Так иных значений на конической области функция принимать не может, то общее решение имеет вид
– произвольная функция числового аргумента ξ (см. напр. [8]). Так иных значений на конической области функция принимать не может, то общее решение имеет вид
![]()
![]()
Решение (II. a, II. b). Коническая область должна содержать ось Oa по условию. На этой оси функция F постоянна и равна 0 или 1, так как ![]() . Общее непрерывное решение – константа 0 или 1.
. Общее непрерывное решение – константа 0 или 1.
Решение. Верно тождество ![]() Следовательно, на луче Oa, а>0, функция имеет вид
Следовательно, на луче Oa, а>0, функция имеет вид ![]() Из уравнения следует, что значения функции
Из уравнения следует, что значения функции ![]() на линиях уровня представляющие собой либо эллипсы, либо гиперболы, либо вертикальные прямые (при
на линиях уровня представляющие собой либо эллипсы, либо гиперболы, либо вертикальные прямые (при ![]() ), равны т.е.
), равны т.е. ![]() является базовым решением. Общее решение уравнения имеет вид
является базовым решением. Общее решение уравнения имеет вид
![]()
и определено на конической области положительности
![]()
III. a) ![]()
Решение. На луче ![]() . Следовательно
. Следовательно ![]() Для любого а выполнено
Для любого а выполнено ![]() т.е. общее решение
т.е. общее решение ![]()
III. b) ![]()
Решение. Функция ![]() является решением.
является решением.
- Если
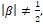 то рассмотрим функцию
то рассмотрим функцию 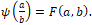 Для нее выполнено
Для нее выполнено 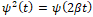 . Тогда
. Тогда 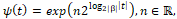 ([4], стр. 114), и общее решение имеет вид
([4], стр. 114), и общее решение имеет вид 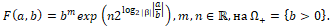
- Если
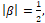 то определим функцию
то определим функцию 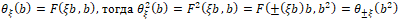 . Все решения имеют вид
. Все решения имеют вид 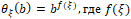 – произвольная функция числового аргумента ξ для знака плюс, и четная – для знака минус. Общее решение имеет вид
– произвольная функция числового аргумента ξ для знака плюс, и четная – для знака минус. Общее решение имеет вид 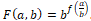 .
.
III. c) ![]()
Решение. Первым базовым решением, очевидно, является функция ![]() . Для нахождения второй базовой функции рассмотрим функцию вида
. Для нахождения второй базовой функции рассмотрим функцию вида ![]() .
.
![]()
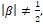 В этом случае можно сделать замену
В этом случае можно сделать замену
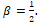 Задав произвольную функцию
Задав произвольную функцию 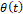 на промежутке [0, 1) и используя тождество
на промежутке [0, 1) и используя тождество 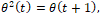 продолжим её на промежуток и т.д. При выполнении граничных условий, можно добиться непрерывности и гладкости построенной функции. Общее решение исходного уравнения будет иметь вид
продолжим её на промежуток и т.д. При выполнении граничных условий, можно добиться непрерывности и гладкости построенной функции. Общее решение исходного уравнения будет иметь вид
- Снова
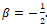 рассмотрим функцию вида
рассмотрим функцию вида 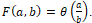 .
.
Следовательно, непрерывные решения только ![]() . Общее решение
. Общее решение ![]()
III. d) ![]()
Решение. Функция ![]() является решением. Для нахождения второй базовой функции рассмотрим функцию вида
является решением. Для нахождения второй базовой функции рассмотрим функцию вида ![]() .
.
i) При ![]() очевидное общее решение
очевидное общее решение ![]()
ii) При ![]() зададим на промежутке
зададим на промежутке ![]() произвольную функцию
произвольную функцию ![]() и пользуясь соотношением будем доопределять ее последовательно на промежутках
и пользуясь соотношением будем доопределять ее последовательно на промежутках ![]() В силу условия
В силу условия ![]() эти промежутки покроют всю полуось. Общее решение на конической области
эти промежутки покроют всю полуось. Общее решение на конической области ![]() имеет вид
имеет вид ![]()
iii) При ![]() сделаем замену
сделаем замену ![]() – любой корень уравнения
– любой корень уравнения ![]() Тогда
Тогда ![]() . Положив
. Положив ![]() мы получим уравнение Шрёдера
мы получим уравнение Шрёдера ![]()
Теорема 7 ([5], п. 6.5.24, стр. 122). Пусть ![]() строго возрастает,
строго возрастает, ![]() тогда единственным непрерывным решением уравнения
тогда единственным непрерывным решением уравнения
на отрезке ![]()
Доказательство этой теоремы можно найти в [6, 7]. Для гладкой строго возрастающей функции ![]() называющейся ядром, условия теоремы будут выполнены на некотором промежутке при
называющейся ядром, условия теоремы будут выполнены на некотором промежутке при ![]() Применительно к нашему уравнению это условие запишется как
Применительно к нашему уравнению это условие запишется как ![]() что выполнено только для левого корня при
что выполнено только для левого корня при ![]()
Решение. Функция F равна 1 или 0 тождественно на оси Ob, следовательно в любой точке ![]() значение
значение ![]() есть 0 или 1.
есть 0 или 1.
Решение. Рассмотрим функцию ![]()
![]()
Общее решение имеет вид ![]() где в случае знака минус аргумент
где в случае знака минус аргумент ![]() . Определим свойства функции
. Определим свойства функции ![]() подставив в исходное равенство
подставив в исходное равенство
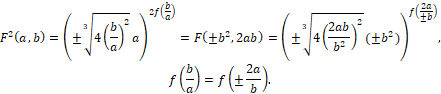
- i) (+). Задав любую
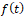 функцию на промежутке
функцию на промежутке 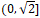 и по указанному равенству продолжив на
и по указанному равенству продолжив на 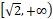 мы получим искомую функцию.
мы получим искомую функцию. - ii) (-). Задав любую
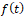 функцию на промежутке
функцию на промежутке 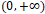 и по указанному равенству продолжив на
и по указанному равенству продолжив на 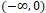 мы получим искомую функцию.
мы получим искомую функцию.
Итак, общее решение
![]()
Решение. i) При ![]() уравнение имеет очевидное общее решение
уравнение имеет очевидное общее решение
- При
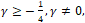 рассмотрим
рассмотрим 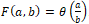 .
.
Обозначим ![]() корни квадратного уравнения
корни квадратного уравнения ![]() Сделав замены
Сделав замены ![]() мы получим два уравнения Шрёдера ([9])
мы получим два уравнения Шрёдера ([9]) ![]() Применим стандартную схему рассуждений ([8]), сделав подстановку
Применим стандартную схему рассуждений ([8]), сделав подстановку ![]() например, в первое уравнение
например, в первое уравнение
При ![]() одно из отношений
одно из отношений ![]() строго меньше единицы и соответствующее уравнение Шрёдера имеет лишь тривиальное решение. Для второго отношения (будем считать, что
строго меньше единицы и соответствующее уравнение Шрёдера имеет лишь тривиальное решение. Для второго отношения (будем считать, что ![]() – правый корень) применим теорему 7 к уравнению
– правый корень) применим теорему 7 к уравнению![]() обладает свойствами:
обладает свойствами: ![]() По теореме 7, решение тривиально на указанном отрезке.
По теореме 7, решение тривиально на указанном отрезке.
Решение. i) При ![]() уравнение имеет очевидное решение
уравнение имеет очевидное решение ![]() . Для поиска остальных решений запишем
. Для поиска остальных решений запишем ![]()
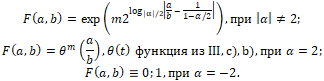 ii) При
ii) При Завершение описания гладких общих решений уравнений Бетхера второго порядка состоит в решении пяти оставшихся не решёнными канонических уравнений. Перечислим уравнения от одной переменной, к которым они сводятся:
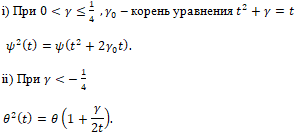
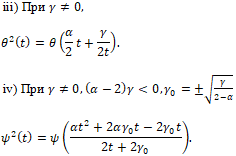
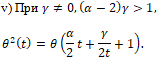
Перечисленные уравнения могут быть интерпретированы как вопрос о вещественной сопряженности многочлена t2 и рациональной функции (ядра). Полное решение этого вопроса в комплексном случае можно найти в [10].
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Кальницкий В.С. Локальные гладкие сопряжения эндоморфизмов Фробениуса / В.С. Кальницкий, А.Н. Петров // Записки науч. сем. ПОМИ. – 2018. – T. 476. – С. 111-124.
- Кальницкий В.С. Связь уравнения Бетхера с параметризованным интегралом Пуассона / В.С. Кальницкий, А.Н. Петров // Вестник Санкт-Петербургского университета. Математика. Механика. Астрономия. – 2018. – 5(63). – С. 614-622.
- Horn R. A. Matrix Analysis / R. A. Horn, C. R. Johnson // Cambridge University Press. – 1985. – 561 P.
- Пелюх Г.П. Метод инвариантов в теории функциональных уравнений / Г.П. Пелюх, А.Н. Шарковский // Працi Iнституту математики НАНУ. Т. 95 – Киев: Инст. мат. НАН, Украина, 2013. – 255 с.
- Нечепуренко М.И. Итерации вещественных функций и функциональные уравнения / М.И. Нечепуренко. – Новосибирск, 1997. – 228 с.
- Dyjak C. BV-solution of a linear functional equation / C. Dyjak // Publ. Math. – 1986. – 33, N 1-2. – P. 83-85.
- Matkowski J.A. Solutions of bounded variation of a linear functional equation / J.A. Matkowski, M.A. Zdun // Aequat. Math. – 1974. – 10, N 2,3. – P. 223-235.
- Полянин А.Д. Справочник по интегральным уравнениям: Точные решения / А.Д. Полянин, А.В. Манжиров. – Москва: Факториал, 1998. – 432 с.
- Schroeder E. Über iterirte Funktionen / E. Schroeder // Math. Ann. – 1871. – 3. – P. 296-322.
- Еременко А.Э. О некоторых функциональных уравнениях, связанных с итерацией рациональных функций / А.Э. Еременко // Алгебра и анализ. – 1989. – Т. 1, Вып. 4. – С. 102–116.
Список литературы на английском языке / References in English
- Kalnitsky V.S. Lokal'nye gladkie soprjazhenija jendomorfizmov Frobeniusa [Local smooth conjugations of Frobenius endomorphisms] / V.S. Kal'nickij, A.N. Petrov // Zapiski nauch. sem. POMI [Journal of mathematical sciences]. – 2020. – v. 251, No. 4. – p. 503-511. [in Russian]
- Kalnitsky V.S. Svjaz' uravnenija Bethera s parametrizovannym integralom Puassona [Relation of the Böttcher Equation with the parametrized Poisson Integral] / V.S. Kal'nickij, A.N. Petrov // Vestnik Sankt-Peterburgskogo universiteta. Matematika. Mehanika. Astronomija [Vestnik St. Petersburg University: Mathematics]. – 2018. – 51 (4). – p. 373-379. [in Russian]
- Horn R. A. Matrix Analysis / R. A. Horn, C. R. Johnson // Cambridge University Press. – 1985. – 561 P.
- Peluh G.P. Metod invariantov v teorii funkcional'nyh uravnenij [Method of invariants in the functional equations theory] / G.P. Peljuh, A.N. Sharkovskij // Praci institutu matematiki NAS Ukrainy. V. 95 – Kyiv: Inst. of Math. NASU, 2013. – 255 p. [in Russian]
- Nechepurenko M.I. Iteracii veshhestvennyh funkcij i funkcional'nye uravnenija [Real functions iterations and functional equations] / M.I. Nechepurenko. – Novosibirsk, 1997. – 228 p. [in Russian]
- Dyjak C. BV-solution of a linear functional equation / C. Dyjak // Publ. Math. – 1986. – 33, N 1-2. – P. 83-85.
- Matkowski J.A. Solutions of bounded variation of a linear functional equation / J.A. Matkowski, M.A. Zdun // Aequat. Math. – 1974. – 10, N 2,3. – P. 223-235.
- Polyanin, A. D. Spravochnik po integral'nym uravnenijam: Tochnye reshenija [Handbook of Integral Equations: Exact Solutions (Supplement. Some Functional Equations)] / A.D. Poljanin, A.V. Manzhirov. – Moscow: Faktorial, 1998. – 432 P. [in Russian]
- Schroeder E. Über iterirte Funktionen [About iterated functions] // Math. Ann. – 1871. – 3. – P. 296-322. [in German]
- Eremenko A.E. O nekotoryh funkcional'nyh uravnenijah, svjazannyh s iteraciej racional'nyh funkcij [On some functional equations related to the iteration of rational functions] / A.Je. Eremenko // Algebra i analiz [Algebra and Analysis]. – 1989. – V. 1, Issue. 4. – P. 102–116. [in Russian]
