К ИССЛЕДОВАНИЮ КВАЗИГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА С НЕЛИНЕЙНОСТЬЮ, ОБЛАДАЮЩЕЙ НАСЫЩЕНИЕМ
К ИССЛЕДОВАНИЮ КВАЗИГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА С НЕЛИНЕЙНОСТЬЮ, ОБЛАДАЮЩЕЙ НАСЫЩЕНИЕМ
Научная статья
Антоновская О.Г.1, *, Бесклубная А.В.2
1 ORCID: 0000-0002-5688-7996;
1, 2 Нижегородский государственный архитектурно-строительный университет, Нижний Новгород, Россия
* Корреспондирующий автор (olga.antonovsckaja[at]yandex.ru)
АннотацияВесьма эффективным средством исследования колебательных процессов в различных разделах физики и техники является аппарат теории дифференциальных уравнений. Естественно, наиболее доступными для исследования являются колебательные системы с малой нелинейностью. Причем до сих пор особый интерес представляет изучение систем, близких к гармоническому осциллятору (квазигармонический осциллятор). В настоящей работе приведен пример исследования квазигармонического осциллятора (с нелинейностью, обладающей насыщением) методом приближенных точечных отображений. Вопрос о его синхронизации сводится к решению вопроса о существовании неподвижных точек точечного отображения, при построении которого применяется метод последовательных приближений. Обсуждается вопрос о локальной применимости результатов приближенного исследования.
Ключевые слова: квазигармонический осциллятор, насыщение нелинейности, малый параметр, асимптотические методы исследования, метод точечных отображений.
ON STUDY OF QUASIHARMONIC OSCILLATOR WITH NONLINEARITY AND SATURATION
Research article
Antonovskaya O.G.1, *, Besklubnaya A.V.2
1 ORCID: 0000-0002-5688-7996;
1, 2 Nizhny Novgorod State University of Architecture, Building and Civil Engineering, Nizhny Novgorod, Russia
* Corresponding author (olga.antonovsckaja[at]yandex.ru)
AbstractThe apparatus of the theory of differential equations is a very effective means for studying oscillatory processes in various branches of physics and technology. Naturally, the most accessible for investigation are oscillatory systems with low nonlinearity. Moreover, the study of systems close to a harmonic oscillator (quasi-harmonic oscillator) is still of particular interest. In this paper, we give an example of the study of a quasi-harmonic oscillator (with non-linearity with saturation) by the method of approximate point mappings. The question of its synchronization is reduced to solving the question of the existence of fixed points of a point mapping, in the construction of which the method of successive approximations is applied. The question of the local applicability of the results of an approximate study is discussed in the paper.
Keywords: quasiharmonic oscillator, nonlinearity saturation, small parameter, asymptotic research methods, point mapping method.
В настоящее время нет необходимости обосновывать важное значение колебательных процессов в современной физике и технике [1, C. 9]. Обнаружение и изучение колебательных закономерностей явлений различной физической природы составляют основные задачи теории нелинейных колебаний. В реальных системах отыскание колебаний, которые могут быть как желательными, так и нежелательными, является важной практической проблемой. А теория колебаний есть ветвь прикладной математики, которая едиными математическими методами исследует динамику различных объектов. В трудах по теории колебаний мощным инструментом исследования стали дифференциальные уравнения [1], [2]. Естественно, что на первом этапе развития теории колебаний исследователи стремились изучаемые ими колебательные процессы подводить под линейные схемы [2, С. 11-16]. Однако многочисленные исследования показали принципиальное отличие механики нелинейных колебаний от механики линейных колебаний (даже в случае малой нелинейности) [2, С. 13-18]. Поэтому возникает необходимость других подходов к решению нелинейных проблем. Например, каждая конкретная задача (или целый класс задач) трактуется уже как нелинейная, но индивидуально, с применением наиболее к ней подходящего метода, или с учетом некоторой ее специфики [1, С. 11]. Зато такой подход означает достаточное математическое обоснование каждой проблемы. Кроме того, следует отметить, что всякое описание реальной физической системы с помощью математических соотношений основано на некоторой идеализации ее свойств. Причем идеализация эта зависит не только от свойств рассматриваемой системы, но и от того, ответы на какие вопросы нужно получить.
Под колебательным процессом принято понимать процесс, обладающий той или иной степенью повторяемости. При изучении любой системы особый интерес представляют стационарные движения, т.е. движения, определяющие поведение системы в течение длительных промежутков времени. Стационарное движение это как бы предельное движение, к которому стремится система. К таким движениям относятся прежде всего состояния равновесия и периодические движения, которые устойчивы не только по отношению к малым изменениям координат, но и к малым изменениям самих уравнений, описывающих систему (в частности – малым изменениям параметров). Переходные процессы характеризуются тем стационарным движением, к которому они приближаются. Интерес представляет также смена стационарных движений, которая происходит при изменении некоторого параметра системы (бифуркация). Таким образом, целью исследования любой системы является изучение поведения траекторий в фазовом пространстве системы, а также разбиение пространства параметров на области существования различных стационарных движений.
Для слабо нелинейных систем существует немало общих асимптотических методов исследования [2, C. 13-23]. Однако применение их в каждом конкретном случае может вызывать чисто технические трудности. Поэтому, естественно, приходится не только выбирать наиболее подходящий метод исследования такой системы, но и приспосабливать его к особенностям рассматриваемой задачи.
До сих пор представляет интерес изучение систем близких к гармоническому осциллятору (квазигармонический осциллятор) [1, С. 650–663], [2, С. 19–21], [4]. В настоящей работе приведен пример исследования квазигармонического осциллятора (с нелинейностью, обладающей насыщением) методом приближенных точечных отображений [6], [7]. Вопрос о существовании периодических движений при этом сводится к решению вопроса о существовании и устойчивости простых неподвижных точек построенного точечного отображения. Обсуждается вопрос о локальной применимости результатов приближенного исследования. Системы с нелинейностью, обладающей насыщением (т.е. при больших значениях входной величины модуль выходной величины достигает максимального значения, а затем перестает меняться) [3, C. 265-269] играют особую роль в теории систем, поскольку такая ситуация имеет место во многих технических системах.
Согласно, при исследовании динамики синхронизуемого осциллятора
в котором ![]() есть параметр, характеризующий близость системы к гармоническому осциллятору, а
есть параметр, характеризующий близость системы к гармоническому осциллятору, а ![]() – период внешней силы, методом точечных отображений [10], исследование поведения траекторий (1) может быть сведено к изучению точечного отображения T секущей поверхности
– период внешней силы, методом точечных отображений [10], исследование поведения траекторий (1) может быть сведено к изучению точечного отображения T секущей поверхности ![]() фазового пространства
фазового пространства ![]() в себя [6], [7], порожденного траекториями системы. При этом с точностью до величин порядка μ2 точечное отображение
в себя [6], [7], порожденного траекториями системы. При этом с точностью до величин порядка μ2 точечное отображение ![]() может быть приближено точечным отображением T с функциями последования
может быть приближено точечным отображением T с функциями последования
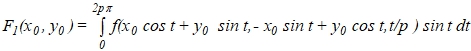 (4)
(4)
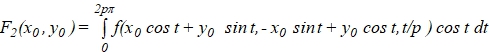 (5)
(5)
Изучение условий существования синхронного режима с периодом внешней силы может быть проведено с помощью изучения условий существования и устойчивости простой неподвижной точки ![]() отображения
отображения ![]() .
.
Особый интерес представляет изучение движений квазигармонического осциллятора вблизи главного резонанса (![]() ). В дальнейшем будем рассматривать квазилинейное дифференциальное уравнение вида
). В дальнейшем будем рассматривать квазилинейное дифференциальное уравнение вида
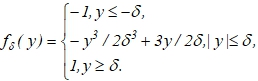 (8)
(8)
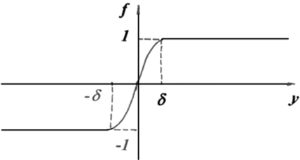
Рис. 1 – Вид нелинейности
Заметим, что функция ![]() является непрерывной и непрерывно дифференцируемой при всех значениях аргумента, параметр
является непрерывной и непрерывно дифференцируемой при всех значениях аргумента, параметр ![]() характеризует близость функции к нелинейности типа
характеризует близость функции к нелинейности типа ![]() (при
(при ![]() стремится к
стремится к ![]() ). Будем искать условия существования у (7) периодического решение с периодом 2π.
). Будем искать условия существования у (7) периодического решение с периодом 2π.
Для системы (7) приближенно построенное отображение ![]() секущей поверхности имеет вид
секущей поверхности имеет вид
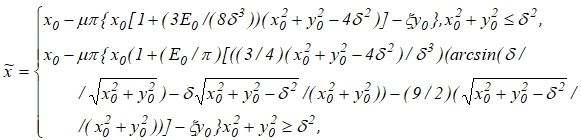
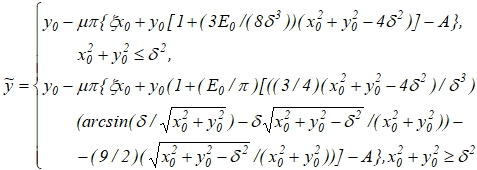 (9)
(9)
т.е. ![]() непрерывно. Следует также отметить, что отображение
непрерывно. Следует также отметить, что отображение ![]() при
при ![]() принимает вид, отвечающий случаю
принимает вид, отвечающий случаю ![]() [6], [7].
[6], [7].
Рассмотрим общий случай, ![]() . Условия
. Условия ![]() дают соотношения
дают соотношения
![]()
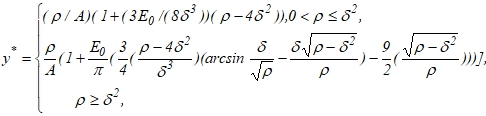 (12)
(12)
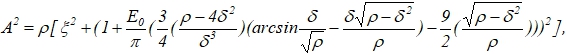 (13)
(13)
![]()
Т.е. неподвижные точки ![]() существуют только в случае существования корней
существуют только в случае существования корней ![]() уравнения (13).
уравнения (13).
Анализ уравнения ![]() резонансной кривой при
резонансной кривой при ![]() и позволяет сделать вывод о существовании при малых A двух ветвей этой кривой (замкнутой и разомкнутой), куски которых, расположенные в областях
и позволяет сделать вывод о существовании при малых A двух ветвей этой кривой (замкнутой и разомкнутой), куски которых, расположенные в областях ![]() , стыкуются при
, стыкуются при ![]() с общей касательной. Причем кривая
с общей касательной. Причем кривая ![]() имеет на плоскости
имеет на плоскости ![]() горизонтальную касательную при
горизонтальную касательную при ![]() , а вертикальную может иметь только в точках кривой К
, а вертикальную может иметь только в точках кривой К
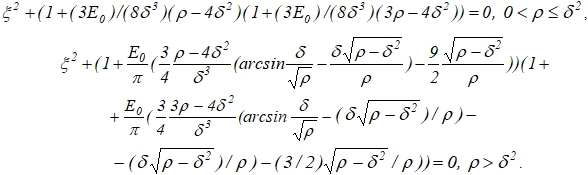 (14)
(14)
Следует отметить, что кривая К лежит в области ![]() .
.
При ![]() (14) есть уравнение эллипса с центром в точке
(14) есть уравнение эллипса с центром в точке ![]() и главными диаметрами
и главными диаметрами ![]() и
и ![]() соответственно. Заметим, что кривая (14) имеет общие точки с областью
соответственно. Заметим, что кривая (14) имеет общие точки с областью ![]() только при
только при ![]() эллипс (14) целиком лежит в полосе
эллипс (14) целиком лежит в полосе ![]() сжимается в точку
сжимается в точку ![]() уравнение кривой К имеет более сложный вид, но это также замкнутая кривая. Примерный вид резонансных кривых в случае
уравнение кривой К имеет более сложный вид, но это также замкнутая кривая. Примерный вид резонансных кривых в случае ![]() для различных
для различных ![]() представлен на рис.2-3.
представлен на рис.2-3.
Устойчивость неподвижных точек (12) отображения ![]() (9) определяется корнями характеристического полинома
(9) определяется корнями характеристического полинома
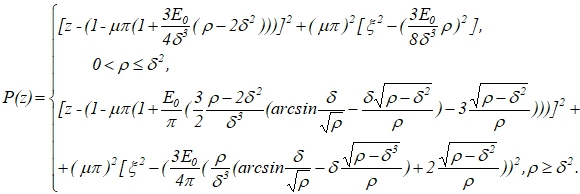
Корни полинома P(z) будут действительными, если выражение, стоящее в квадратных скобках при ![]() , будет отрицательным, и комплексно-сопряженными в случае его положительности. То есть, уравнение границы
, будет отрицательным, и комплексно-сопряженными в случае его положительности. То есть, уравнение границы ![]() появления пары комплексно-сопряженных корней характеристического полинома в этом случае будет иметь вид
появления пары комплексно-сопряженных корней характеристического полинома в этом случае будет иметь вид
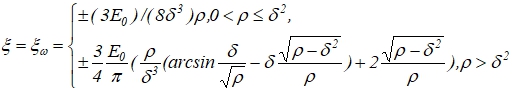 (15)
(15)
причем легко видеть, что отрезки кривых, получаемых по уравнению (15) при ![]() стыкуются при
стыкуются при ![]() с одной и той же касательной
с одной и той же касательной ![]() .
.
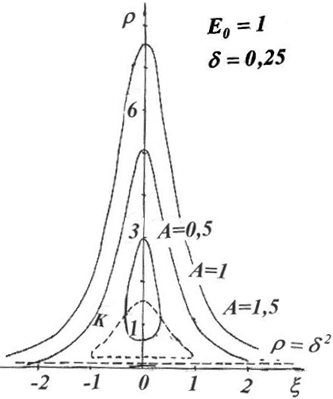
Рис. 2 – Вид резонансных кривых при![]()
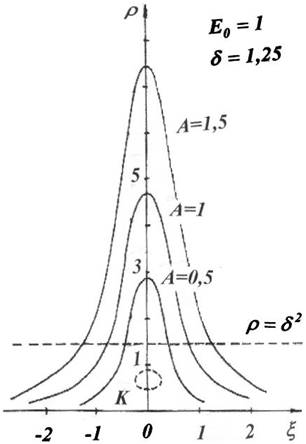
Рис. 3 – Вид резонансных кривых при ![]()
Уравнения границ ![]() области устойчивости на плоскости
области устойчивости на плоскости ![]() могут быть получены методом D-разбиений [11, C. 86-107] и имеют следующий вид. Для
могут быть получены методом D-разбиений [11, C. 86-107] и имеют следующий вид. Для ![]() получаются уравнения, не зависящие от
получаются уравнения, не зависящие от ![]() и совпадающие с уравнениями кривой К (13).
и совпадающие с уравнениями кривой К (13).
Уравнение ![]() есть
есть
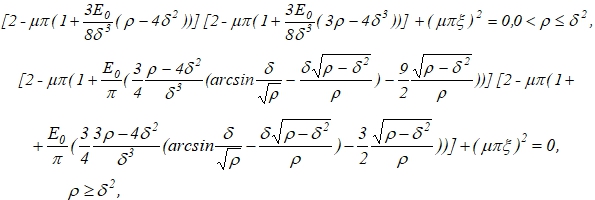 (16)
(16)
причем в случае существования точек кривой ![]() , для которых
, для которых ![]() , отрезки
, отрезки ![]() , соответствующие значениям
, соответствующие значениям ![]() , стыкуются в точках
, стыкуются в точках ![]() с одной и той же касательной.
с одной и той же касательной.
Следует отметить, что при ![]() уравнение границы
уравнение границы ![]() при
при ![]() описывает эллипс с центром в точке
описывает эллипс с центром в точке
![]()
и главными диаметрами ![]()
![]() соответственно. При
соответственно. При ![]() описываемый первым уравнением (16) эллипс всегда лежит в области
описываемый первым уравнением (16) эллипс всегда лежит в области ![]() .
.
Уравнение границы ![]() имеет вид
имеет вид ![]()
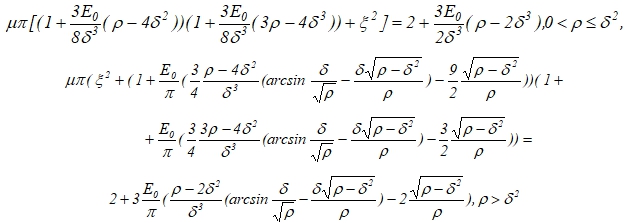 (17)
(17)
Кривая ![]() начинается в точках касания границ
начинается в точках касания границ ![]() , и имеет асимптоты
, и имеет асимптоты ![]() , если
, если ![]() .
.
На рис.4 представлен примерный вид границ D-разбиения для значений ![]() . Область D=0 есть область устойчивости. Факт существования устойчивых неподвижных точек отображения
. Область D=0 есть область устойчивости. Факт существования устойчивых неподвижных точек отображения ![]() при A=const и различных
при A=const и различных ![]() может быть установлен наложением картины поведения границ D-разбиения на плоскости
может быть установлен наложением картины поведения границ D-разбиения на плоскости ![]() при заданном
при заданном ![]() на плоскость с резонансной кривой при заданном A [6], [7].
на плоскость с резонансной кривой при заданном A [6], [7].
Заметим, что ввиду ограниченности нелинейности в формулах точечного отображения ![]() , можно показать, что модель является невырожденной (т.е. бесконечность в приближенной модели, как и в реальной системе, неустойчива) [6; 7, C. 75-78]. Таким образом, если нелинейность в исходной системе ограничена, то в пространстве параметров для любого конечного значения
, можно показать, что модель является невырожденной (т.е. бесконечность в приближенной модели, как и в реальной системе, неустойчива) [6; 7, C. 75-78]. Таким образом, если нелинейность в исходной системе ограничена, то в пространстве параметров для любого конечного значения ![]() существует, хотя и ограниченная по |ξ|, область невырожденности математической модели (при
существует, хотя и ограниченная по |ξ|, область невырожденности математической модели (при ![]() область невырожденности приближенной модели все более расширяется и стремится к
область невырожденности приближенной модели все более расширяется и стремится к ![]() , что соответствует результатам, получаемым численными методами при исследовании исходной системы). Факт существования области невырожденности рассматриваемой приближенной модели связан с тем, что в отличие от случаев с полиномиальной нелинейностью, для случая нелинейности, обладающей насыщением, при
, что соответствует результатам, получаемым численными методами при исследовании исходной системы). Факт существования области невырожденности рассматриваемой приближенной модели связан с тем, что в отличие от случаев с полиномиальной нелинейностью, для случая нелинейности, обладающей насыщением, при ![]() не существует границы
не существует границы ![]() смены устойчивости неподвижных точек
смены устойчивости неподвижных точек ![]() в пространстве параметров.
в пространстве параметров.
В заключение отметим, что предложенная методика исследования основана на применении асимптотических методов. Поэтому по-прежнему актуальной является проблема получения адекватных результатов изучения системы (7) с малым параметром по ее приближенному исследованию [1, C. 650-707], [10, C. 213-218]. Причем речь идет как о количественном, так и о качественном исследовании системы [6], [7, С. 81–88]. Одним из таких методов оценки достоверности сделанных выводов может быть метод, описанный в работах [7, С. 14-35, 12].
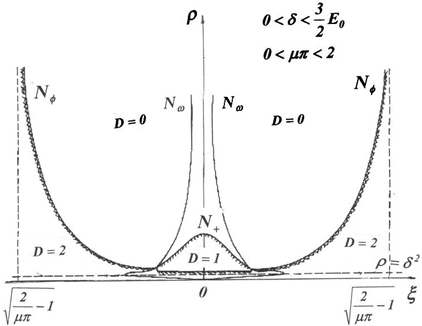
Рис. 4 – Примерный вид границ D-разбиения
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Андронов А. А. Теория колебаний / А. А. Андронов, А. А. Витт, С. Э. Хайкин. – М.: Физматгиз, 1959. – 916 с.
- Боголюбов Н. Н. Асимптотические методы в теории нелинейных колебаний / Н. Н. Боголюбов, Ю. А. Митропольский. – М.: Наука, 1974. – 504 с.
- Пономарев В. М. Основы автоматического регулирования и управления / В.М. Пономарев, А. П. Литвинов. – М.: Высшая школа, 1974. – 439 с.
- Журавлев В. М. Построение огибающей и локальной частоты стохастического процесса на основе модели осциллятора с флуктуирующей частотой / В. М. Журавлев, П. П. Миронов, С. В. Летуновский // Изв. вузов. Поволжский регион. Физико-математические науки. – 2013. –№3(27). – С. 159–169.
- Ивинская Е. Ю. Теоретические аспекты исследования неравновесных экономических систем на основе модели гармонического осциллятора / Е. Ю. Ивинская // Теория и практика общественного развития. Экономические науки. – 2015. – № 21. – С. 57–59.
- Антоновская О. Г. О влиянии насыщения нелинейности на результаты исследования принудительной синхронизации методом приближенных точечных отображений / О. Г. Антоновская // Математическое моделирование и оптимальное управление: Вестник ННГУ, Нижний Новгород. – – № 2(21). – С. 198–208.
- Антоновская О. Г. Метод точечных отображений в задачах нелинейной динамики / О. Г. Антоновская, В. И. Горюнов. – Гамбург: LAP Lambert Academic Publishing, 2013. – 140 с.
- Антоновская О. Г. Об одном случае исследования принудительной синхронизации методом приближенных точечных отображений / О. Г. Антоновская, М. Н. Зайцева // Международный научно-исследовательский журнал. – 2018. – № 8(74). – С. 7–14.
- Антоновская О. Г. Об изложении приложений метода точечных отображений в учебном процессе / О. Г. Антоновская, А. В. Бесклубная // Тенденции развития науки и образования. – 2019. – № 49. – Ч. 1. – С. 12–17.
- Неймарк Ю. И. Метод точечных отображений в теории нелинейных колебаний. / Ю. И. Неймарк. – М.: Наука, 1972. – 472 с.
- Неймарк Ю. И. Динамические системы и управляемые процессы. Изд. 2-е. / Ю. И. Неймарк. – М.: Книжный дом «ЛИБРОКОМ», 2010. – 336 с.
- Антоновская О. Г. О приближенном исследовании близкого к тождественному точечного отображения плоскости в плоскость / О. Г. Антоновская // Математическое моделирование и оптимальное управление: Вестник ННГУ, Нижний Новгород. – 2004. – № 1(27). – С. 63–69.
Список литературы на английском языке / References in English
- Andronov A. A. Teoriya kolebaniy [Vibrations theory] / A. A. Andronov, A. A. Vitt, S. Yu. Haykin. – M.: Fizmatgiz, 1959. – 916 p. [in Russian]
- Bogolyubov N. N. Asimptotichesiye metody v teorii nelineynyh kolebaniy [Asymptotic methods in nonlinear vibrations theory] / N. N. Bogolyubov, A. Yu. Mitropolskiy – M.: Nauka, 1974. – 504 p. [in Russian]
- Ponomarev V. M. Osnovy avtomaticheskogo regulirovaniya I upravleniya [Principles of automatic regulation and control] / V. M. Ponomarev, A. P. Litvinov – M.: Vysshaya shkola, 1974. – 439 p. [in Russian]
- Zhuravlev V. M. Postroeniye ogibayushey b lokalnoy chastity stohasticheskogo protsessa na osnove modeli ossillyatora c fluktuiruyushey chastoty [The construction of envelope and local frequency of stochastic processon the base of oscillator with fluctuating frequency] / V. M. Zhuravlev, P. P. Mironov, S. V. Letunovskiy // Izv. Vuzov. Povolzhskiy region. Fiziko-matematicheskiye nauki. [Higher educational proceedings of Povolzhsky region. Physical and mathematical sciences ] – 2013. – № 3(27) – P. 159–169. [in Russian]
- Ivinskaya E. Yu. Teoreticheskiye aspekty issledovaniya neravnovesnykh ekonomicheskikh system na osnove modeli garmonicheskogo oscillyatora [Teortical aspects of studying non-equlibrium economic systems based on the model of harmonic oscillator] / E. Yu. Ivinskaya // Teoriya I praktika obshestvennogo razvitiya. Ekonomicheskiye nauki [Theory and practice of public development. Economic sciences] – 2015. – № 21 – P. 57–59. [in Russian]
- Antonovskaya O. G. O vliyanii nasysheniya nelineynosti na resultaty issledovaniya prinuditelnoy sinkhronizatsii metodom priblizhennykh tochechnykh otobrazheniy [On the influence of nonlinearity saturation on the results of the forced synchronization received by means of approximate point mappings method] / O. G. Antonovskaya // Matematicheskoye modelirovaniye I optimalnoye upravleniye. Vestnik NNGU [Mathematical modeling and optimal control. NNGU bulletin] , Nizhny Novgorod. – 1999. – № 2(21). – P. 198–208. [in Russian]
- Antonovskaya O. G. Metod tichechnykh otobrazheniy v zadachakh nelineynoy dinamiki [Point mappings method in non-linear dynamics problems]/ O. G. Antonovskaya, V. I. Goryunov. – GmbH: LAP Lambert Academic Publishing, 2013. – 140 p. [in Russian]
- Antonovskaya O. G. Ob odnom sluchae issledovaniya prinuditelnoy sinhronizatsii metodom priblizhennykh tochechnykh otobrazheniy [Investigation of forced synchronization by the method of approximate point mappings] / O. G. Antonovskaya, M. N. Zaytseva // International research journal – 2018. – № 8(74). – P. 7–14. [in Russian]
- Antonovskaya O. G. Ob izlozhenii prilozheniy metoda tochechnykh otobrazheniy v uchebnom protsesse [On giving in account of applications of point mappings method in teaching process] / O. G. Antonovskaya, A. V. Besklunaya // Tendentsii razvitiya nauki I obrazovaniya [Tendencies of science and education development] – 2019. – № 49. – Part 1. – P. 12–17. [in Russian]
- Neymark Yu. I. Metod tichechnykh otobrazheniy v teriyi nelineynykh kolebaniy [Point mappings method in non-linear vibrations theory] / Yu. I. Neymark. – M.: Nauka, 1972. – 472 p. [in Russian]
- Neymark Yu. I. Dinamicheskiye sistemy i upravliaemye protsessy [Dynamical systems and controllable processes] / Yu. I. Neymark. – M.: «LIBROKOM», 2010. – 336 p. [in Russian]
- Antonovskaya O. G. O priblizhennom issledovanii blizkogo k tozhdestvennomu tochechnogo otobrazheniya ploskosti v ploskost [On the approximate study of close to identical point mapping plain to plain] / O. G. Antonovskaya // Matematicheskoye modelirovaniye I optimalnoye upravleniye. Vestnik NNGU [Mathematical modeling and optimal control. NNGU bulletin], Nizhny Novgorod. – 2004. – № 1(27). – 63–69. [in Russian]
