ИССЛЕДОВАНИЕ ВЕРОЯТНОСТНЫХ И КВАЗИ-ВЕРОЯТНОСТНЫХ РАСПРЕДЕЛЕНИЙ С ПОМОЩЬЮ СПЕЦИАЛИЗИРОВАННОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Козий А.А.1, Минченко И.И.2, Комарова М.Г.3, Киктенко Е.О.4
1ORCID: 0000-0003-0063-5834, Студент, 2ORCID: 0000-0001-8895-4850, Студент, 3ORCID: 0000-0002-1744-2556, Студент, Московский государственный технический университет им. Н. Э. Баумана, 4ORCID: 0000-0001-5760-441X, Ассистент-преподаватель, Московский государственный технический университет им. Н. Э. Баумана, Научный сотрудник, Математический институт им. В.А. Стеклова Российской академии наук
Авторы работы выражают глубокую благодарность Скуйбину Б.Г. за предоставленную возможность выполнения работы в рамках проекта студенческой экспериментальной лаборатории физики (СЭЛФ) МГТУ им. Н.Э. Баумана. Работа К.Е.О. выполнена при поддержке гранта Президента Российской Федерации № MK-2815.2017.1.
ИССЛЕДОВАНИЕ ВЕРОЯТНОСТНЫХ И КВАЗИ-ВЕРОЯТНОСТНЫХ РАСПРЕДЕЛЕНИЙ С ПОМОЩЬЮ СПЕЦИАЛИЗИРОВАННОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Аннотация
Приведены теоретические сведения о функциях распределения вероятности и квази-вероятности (функции Вигнера), а также методах их нахождения для различных классических и квантовых задач соответственно. Разработана компьютерная программа, позволяющая моделировать эволюцию функции распределения вероятности и квази-вероятности для различных задач. Продемонстрировано, что вероятностные и квази-вероятностные распределения могут иметь как сходства, так и различия для каждой конкретной задачи.
Ключевые слова: квази-вероятностное распределение, функция Вигнера, свободная частица, квантовый гармонический осциллятор, потенциальная яма с бесконечно высокими стенками.
Koziy A.A.1, Minchenko I.I.2, Komarova M.G.3, Kiktenko E.O.4
1ORCID: 0000-0003-0063-5834, Student, 2ORCID: 0000-0001-8895-4850, Student, 3ORCID: 0000-0002-1744-2556, Student, Bauman Moscow State Technical University, 4ORCID: 0000-0001-5760-441X, Assistant lecturer, Bauman Moscow State Technical University, Research Scientist, Steklov Mathematical Institute of RAS
The authors of the paper express their deep gratitude to Skuibin BG. For the given opportunity to perform work within the framework of the project of the student experimental physics laboratory (SELF) MSTU. N.E. Bauman. The work of K.E.O. Was supported by the grant of the President of the Russian Federation No. MK-2815.2017.1.
STUDY OF PROBABLE AND QUASI-PROBABLE DISTRIBUTIONS WITH THE HELP OF SPECIALIZED SOFTWARE
Abstract
The article provides theoretical information on probability and quasi-probability (Wigner functions) distribution functions, as well as on the methods for finding them for various classical and quantum problems, respectively. We developed a computer program that enables the modeling of the evolution of the probability and quasi-probability distribution function for various problems. It is demonstrated that probable and quasi-probable distributions can have both similarities and differences for each particular problem.
Keywords: quasi-probability distribution, Wigner function, free particle, quantum harmonic oscillator, potential well with infinitely high walls.
Введение
Функция распределения вероятности в фазовом пространстве (пространстве координат и импульсов) представляет собой эффективный метод описания поведения частиц в классической механике [1]. Использование аппарата теории вероятности в этом случае обычно обусловлено неизбежным наличием погрешности при задании начального состояния частицы, связанным с конечной разрешающей способностью реальных приборов.
Ситуации меняется коренным образом при переходе к квантовой механике, в которой ограничения на точность одновременного определения координаты и импульса связаны уже фундаментальным принципом неопределенности Гейзенберга. Обычно для описания частиц в квантовой механике используются волновые функции (в общем случае матрицы плотности), с помощью которых возможно получить функции распределения вероятности для координаты и импульса по-отдельности [2].
Тем не менее, существуют также альтернативные способы описания квантовых частиц, в том числе с точки зрения их положения в фазовом пространстве. Однако, в отличие от классических частиц, для которых распределения вероятностей представляют собой неотрицательные, нормированные на единицу функции, в квантовом случае сохраняется лишь требование нормированности, в то время, как сама функция распределения может принимать в том числе и отрицательные значения. Именно поэтому, говорится о квази-вероятностных распределениях.
Важнейшим примером функции распределения квази-вероятности является функция Вигнера [3], задаваемая в одномерном случае выражением
![]() (1)
(1)
где ψ – волновая функция, зависящая от координаты и времени, – приведенная константа Планка, x – координата, p – импульс, t – время. Важно отметить, что отрицательность функции Вигнера для определенных значений координаты и импульса свидетельствует о явном проявлении квантовых свойств данной системой [4].
Функции распределения вероятности отдельно по координате и импульсу могут быть получены по формулам, аналогичным формулам для классических совместных распределений:
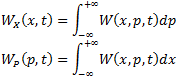
В настоящей работе рассматривалась задача о получении функции распределения (квази-) вероятности ![]() для различных параметров, определяющих (квази-) вероятностного распределения
для различных параметров, определяющих (квази-) вероятностного распределения ![]() в начальный момент времени. Отметим, динамика классического распределения вероятности может быть получена по формуле
в начальный момент времени. Отметим, динамика классического распределения вероятности может быть получена по формуле
![]()
где ![]() – начальное распределение,
– начальное распределение, ![]() – координата и импульс частицы в момент времени t, при условии, что в начальный момент времени частица имела координату x0 и импульс p0.
– координата и импульс частицы в момент времени t, при условии, что в начальный момент времени частица имела координату x0 и импульс p0.
Динамика функции Вигнера для квантовых квази-вероятнотных распределений была получена путем решения соответствующего уравнения Шредингера и подстановки волновой функции в определение (1).
Описание программы
Для решения и моделирования поставленных задач была разработано специализированное программное обеспечение, позволяющие изучать конкретную интересующую задачу с определенными начальными параметрами. Всего было рассмотрено три задачи:
- свободная частица;
- частица в гармоническом потенциале;
- частица в потенциальной яме с бесконечно высокими стенками.
Каждая из задач соответственно была рассмотрена в рамках классической и квантовой механики.
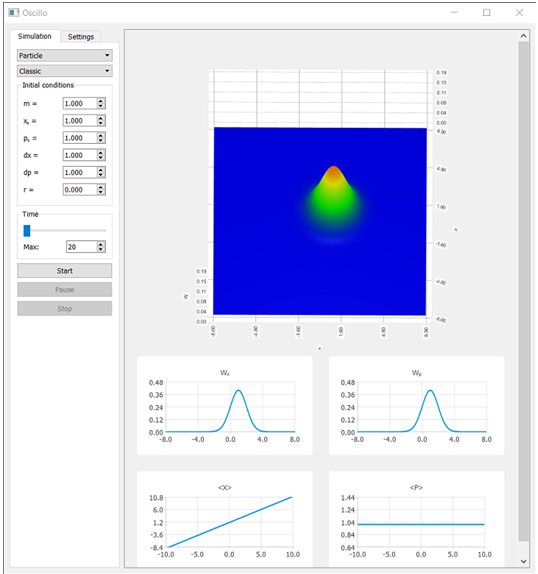
Рис. 1 – Пример интерфейса программы
На Рис. 1 представлен пример работы программы. В центральной области расположен трехмерный график
(квази-) вероятностного распределения. Ниже центральной области прорисовываются графики одномерного распределения (Wx и Wp) и средние значения (![]() ) по координате и импульсу. В левом верхнем углу выбирается интересующая задача и ее тип – классическая или квантовая. Ниже располагается область установления начальных значений – «Initial conditions». Разным задачам соответствуют разные переменные в этой области. Еще ниже находится область управления временем моделирования – «Time». Задавая значение «Max» можно варьировать время, в течении которого будет записываться в память программы динамика функции вероятности. Это дает возможность просматривать тот временной отрезок, который представляет наибольший интерес для наблюдателя. Функция перемотки осуществляется ползунком. Кнопки «Start», «Pause», «Stop» - используются для старта, приостановки, завершения моделирования соответственно.
) по координате и импульсу. В левом верхнем углу выбирается интересующая задача и ее тип – классическая или квантовая. Ниже располагается область установления начальных значений – «Initial conditions». Разным задачам соответствуют разные переменные в этой области. Еще ниже находится область управления временем моделирования – «Time». Задавая значение «Max» можно варьировать время, в течении которого будет записываться в память программы динамика функции вероятности. Это дает возможность просматривать тот временной отрезок, который представляет наибольший интерес для наблюдателя. Функция перемотки осуществляется ползунком. Кнопки «Start», «Pause», «Stop» - используются для старта, приостановки, завершения моделирования соответственно.
Во вкладке «Settings» устанавливаются дополнительные параметры, отвечающие за вывод программы. К ним относятся размеры наблюдаемой области фазового пространства, качество прорисовки трехмерного и двумерных графиков. Также можно устанавливать сглаживание трехмерного графика, отображение сетки и изменять стиль рабочего окна. Кроме того, доступен режим, переводящий промоделированную задачу в режим презентации.
Далее мы более подробно остановимся на каждой из рассмотренных задач.
Классическая свободная частица
Движение классической свободной частицы определяется выражениями
![]()
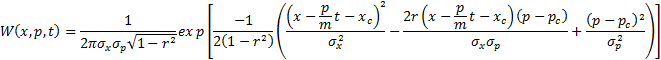
где σx и σp – среднеквадратичные отклонения по координате и импульсу, r – коэффициент корреляции, xc и pc – средние значения координаты и импульса в начальный момент времени.
В физике волн известно понятие дисперсии волнового пакета, отвечающее за скорость расплывания волнового пакета. Причиной расплывания является различие фазовых скоростей составляющих его волн, вследствие чего более быстрые волны уходят вперед, а более медленные отстают [5]. Примечательно, что волновой пакет не обязательно должен растягиваться. В программе имеется возможность продемонстрировать эффект сжатия волнового пакета за счет выбора отрицательного коэффициента корреляции. Для этого необходимо задать отрицательное значение корреляции (см. Рис. 2). Часть распределения с большими значениями импульсов находится левее части с меньшими значениями импульсов. По этой причине должно произойти сжатие и последующее растяжение волнового пакета, так как с течением времени часть распределения с большими значениями импульсов должна уходить правее части с меньшими значениями импульсов.
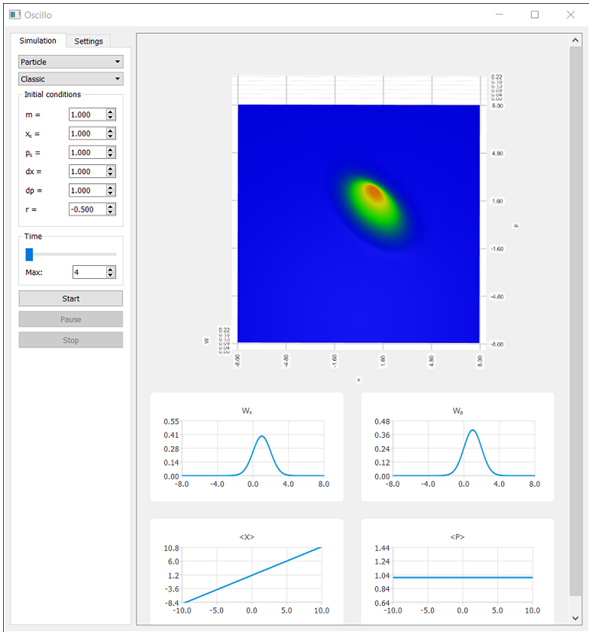
Рис. 2 – Функция вероятности для классической свободной частицы при t=0c; входные параметры: ![]()
Квантовая свободная частица
Начальное состояние частицы описывается следующей волновой функцией:
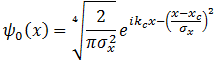
где kc - среднее значение волнового вектора.
Функция Вигнера для такой волновой функции имеет вид двумерного нормального распределения
![]()
Таким образом, классическая и квантовая свободные частицы с точки зрения вероятностного рассмотрения ведут себя схожим образом. Тем не менее, между алгоритмами вычисления и моделирования обеих задач существует важное отличие: для классической задачи возможно задавать произвольные значения неопределенности по координате и импульсу, в случае квантовой задачи неопределенность по импульсу получается автоматически, так как в расчетах используется волновая функция, несущая себе заложенный принцип неопределенности.
Классический гармонический осциллятор
Примером гармонического осциллятора в классической физике является система из закрепленной пружины, за которую зацеплен груз. Если такую систему вывести из положения равновесия, то она придет в колебательное движение, совершаемое по закону синуса или косинуса. В фазовом пространстве траектория движения частицы будет представлять собой эллипс. Функция вероятности имеет следующий вид:
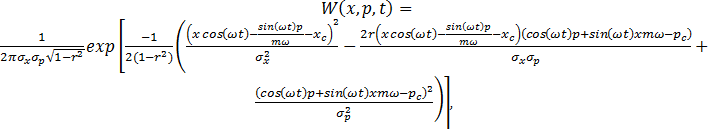
где ω – циклическая частота колебаний.
Пример визуализации функции вероятности для классического гармонического осциллятора представлен на Рис. 3.
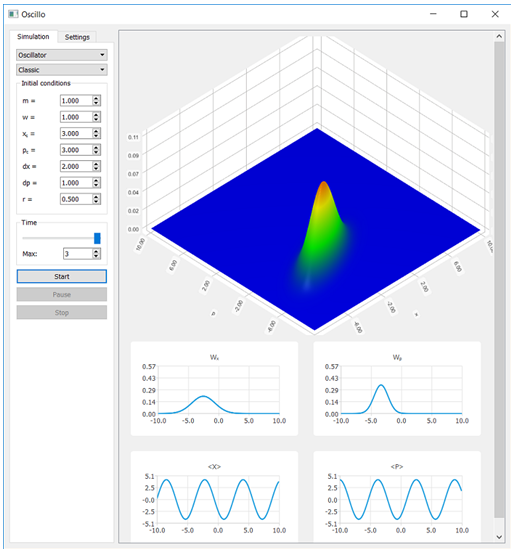
Рис. 3 – Функция вероятности для классического гармонического осциллятора при t=3c; входные параметры: ![]()
Квантовый гармонический осциллятор
Из решения уравнения Шредингера для стационарных состояний были получены волновые функции, в состав которых входят полиномы Эрмита. Был произведен расчет и моделирование функции Вигнера для первых пяти (нулевое состояние и четыре ненулевых) состояний. Для примера, функция Вигнера для третьего стационарного состояния имеет вид:
![]()
где ![]() – перенормированная координата и импульс.
– перенормированная координата и импульс.
Пример визуализации функции квази-вероятности для квантового гармонического осциллятора n=3 представлен на Рис. 4:
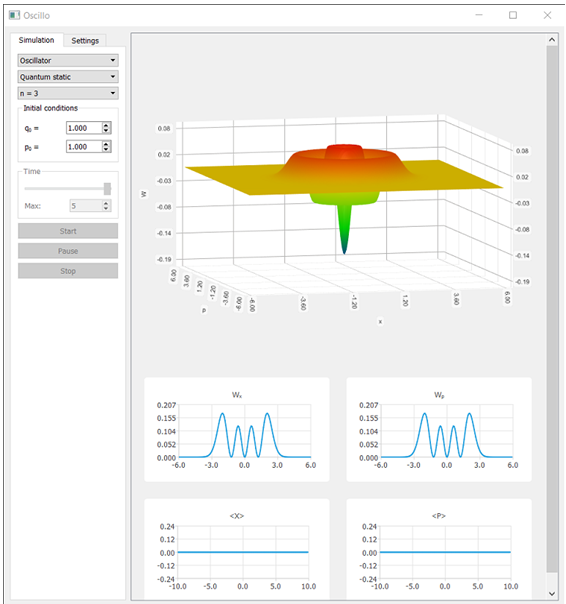
Рис. 4 – Функция квази-вероятности для третьего (n=3) стационарного состояния квантового гармонического осциллятора
Динамические состояния системы могут быть получены из стационарных состояний путем их линейной комбинации:
![]()
где ![]() – стационарная функция, Cn – коэффициенты линейного разложения, En – энергия, соответствующая данному состоянию.
– стационарная функция, Cn – коэффициенты линейного разложения, En – энергия, соответствующая данному состоянию.
В программе реализовано моделирование функции Вигнера, состоящей из первых четырех стационарных состояний (одно нулевое состояние и три ненулевых).
Визуализация функции квази-вероятности для динамических состояний в квантовом гармоническом осцилляторе представлена на Рис. 5.
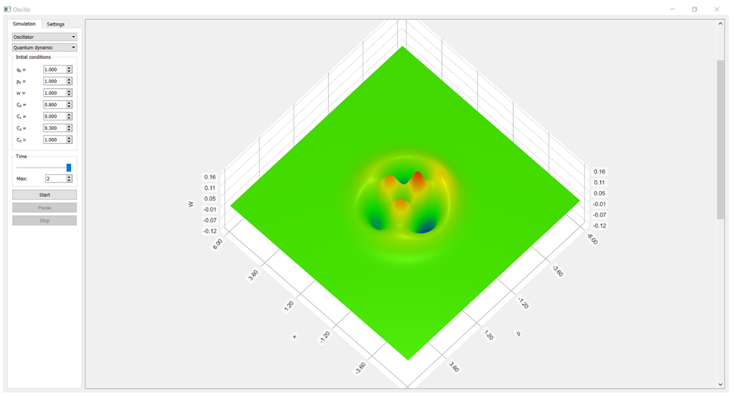
Рис. 5 – Функция квази-вероятности для динамического состояния квантового гармонического осциллятора (![]() ; входные параметры:
; входные параметры: ![]()
Комбинации стационарных состояний с различными коэффициентами могут давать очень различающиеся по форме квази-вероятностные распределения. Так же возможно создать состояние, динамика которого будет аналогична динамике классического гармонического осциллятора. Для этого необходимо воспользоваться распределением Пуассона. Визуализация функции квази-вероятности для динамического Пуассоновского состояния в квантовом гармоническом осцилляторе представлена на Рис. 6.
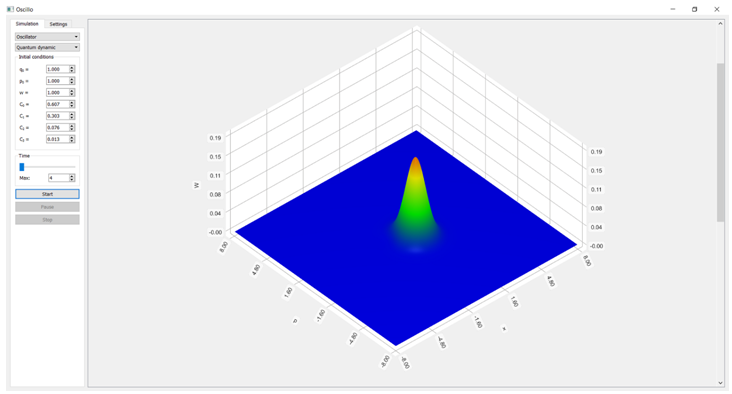
Рис. 6 – Функция квази-вероятности для динамического когерентного состояния квантового гармонического осциллятора
Классический и квантовый гармонические осцилляторы обладают существенно большими различиями, чем классическая и квантовая свободные частицы. На графиках можно заметить, что с классическим распределением совпадает только нулевое стационарное и динамическое Пуассоновское состояние квантового гармонического осциллятора (когерентное состояние). Остальные же состояния имеют гораздо более сложную структуру. Особенностью остальных состояний является то, что функция квази-вероятностного распределения принимает отрицательные значения. В классическом случае отрицательная плотность вероятности лишена смысла. Тем не менее, даже из функции вероятности, которая принимает отрицательные значения, получаются одномерные функции распределения, которые принимают только положительные значения.
Классическая частица в потенциальной яме с бесконечно высокими стенками
В классической задаче рассматривается динамика свободной частицы внутри потенциальной ямы, с учетом, что все удары частицы о стенку являются абсолютно упругими. После каждого отражения частицы о стенку, ее импульс будет меняться на противоположный (изменяется направление движения частицы). Динамика функции вероятности для свободной частицы в потенциальной яме по виду аналогична динамике функции вероятности для свободной частицы, но с учетом отражения от границ ямы.
С течением времени частица будет стремиться к «равномерному заполнению» потенциальной ямы по координате. Это значит, что вероятности найти ее в двух одинаковых по размеру областях по координате должны совпадать. Распределение по импульсу, напротив, должно сосредотачиваться относительно двух значений: и .
Визуализация функции вероятности для свободной частицы в потенциальной яме с бесконечно высокими стенками представлено на Рис. 7.
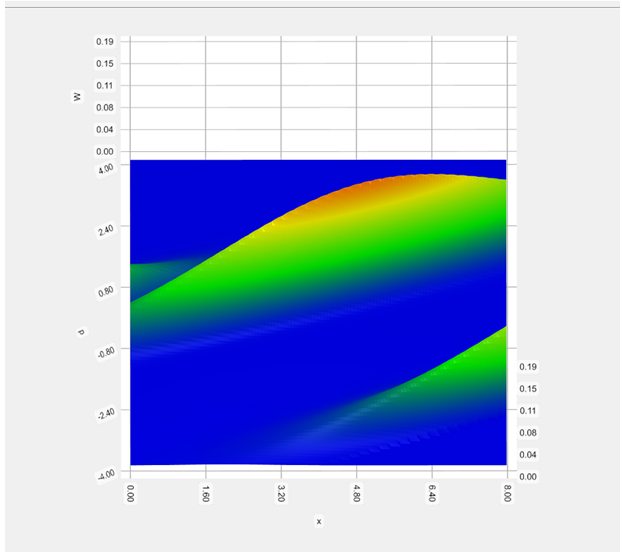
Рис. 7 – Функция вероятности для классической свободной частицы в потенциальной яме с бесконечно высокими стенками при t=3c; входные параметры: ![]()
Квантовая частица в потенциальной яме с бесконечно высокими стенками
Волновые функции, описывающие стационарные состояния в потенциальной яме с бесконечно высокими стенками выглядят следующим образом:
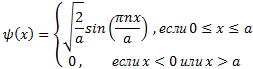
где α – ширина потенциальной ямы, n – номер стационарного состояния.
Функция Вигнера для такой волновой функции представляется достаточно объемной. Ее характерной особенностью является симметрия относительно центра ямы (в фазовом пространстве это симметрия относительно прямой ![]() )
)
Визуализация функции квази-вероятности для квантовой свободной частицы в потенциальной яме с бесконечно высокими стенками:
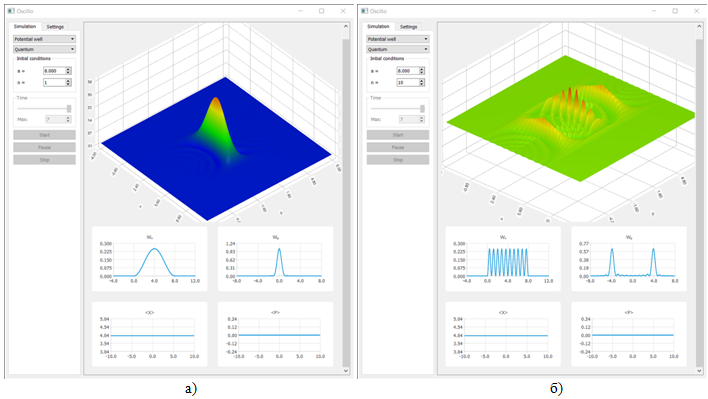
Рис. 8 – Функция квази-вероятности для стационарных состояний квантовой частицы в потенциальной яме с бесконечно высокими стенками: а) Первое состояние (n=1); б) Десятое состояние (n=10); Входные параметры: a = 8
Классическая и квантовая потенциальная яма имеют между собой большие различия. В классической задаче высота стенок не имеет большого значения, важно лишь то, чтобы энергия частицы была меньше, чем высота стенок ямы. При увеличении высоты стенок ничего не меняется. В квантовом случае высота стенок имеет большое значение, потому что при таком условии можно говорить о полной локализации частицы в области ямы. Ни один из полученных графиков для квантовой задачи не обладает сходством с классической задачей. Тем не менее, сходства проявляются при рассмотрении одномерных распределений по координате и импульсу. При больших квантовых числах происходят очень быстрые осцилляции распределения Wx, что можно в пределе рассматривать как равномерное заполнение потенциальной ямы (квази-равномерное), и выделение двух симметричных относительно нулевого импульса пиков в распределении Wp. Это явление можно связать с принципом неопределенности. Для большого квантового числа, число осцилляций распределения по координате увеличивается, что говорит о том, что координату можно определять более точно. Значит, если координата сосредотачивается в малой области, то импульс должен наоборот рассредоточиваться. Что и происходит на полученном графике. Одним из интересных элементов при моделировании квантовой задачи является "рябь" на фазовом пространстве, которая имеет сходство с интерференционной картиной.
Заключение
В процессе работы была создана программа, в которой моделируются задачи: "Свободная частица", "Гармонический осциллятор" и "Потенциальная яма с бесконечно высокими стенками" с точки зрения классической и квантовой механики, в которой можно изменять параметры системы, и рассматривать конкретно интересующие случаи. Открытый код программы, а также более подробное математическое описание доступно по ссылке [6].
На основании моделирования было выяснено, что некоторые квантовые системы, такие как «Свободная частица» и «Гармонический осциллятор (нулевое состояние и Пуассоновское состояние)» могут быть описаны с точки зрения классической физики, а при больших значениях главного квантового числа «Потенциальная яма с бесконечно высокими стенками» имеет одномерные распределения по координате и импульсу схожие с одномерными распределениями в «Классической потенциальной яме». Также было получено, что все стационарные состояния «Квантовой потенциальной ямы», и отличные от нулевого стационарные состояния «Квантового гармонического осциллятора» являются абсолютно неклассическими (функция квази-вероятности принимает отрицательные значения).
Список литературы / References
- Ландау Л. Д. Механика / Л. Д. Ландау, Е. М. Лифшиц – 5-е изд. – М.: Физматлит, 2004. –224 с.
- Ландау Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория) / Л. Д. Ландау, Е. М. Лифшиц – 6-е изд. – М.: Физматлит, 2004. – 800 с.
- Wigner E. P. On the quantum correction for thermodynamic equilibrium / E. P. Wigner // Physical Review – 1932. – Vol. 40 (5). – P. 749–759. doi:10.1103/PhysRev.40.749.
- Шляйх В.П. Квантовая оптика в фазовом пространстве / В.П. Шляйх – М.: Физматлит, 2005. – 760 с.
- Матвеев А. Н. Атомная физика / А. Н. Матвеев – М.: Высш. шк., 1989. – 439 с.
- Веб-сервис Bitbucket. – Режим доступа: https://bitbucket.org/iminchenko/oscillo/
Список литературы на английском языке / References in English
- Landau, L. D. Mehanika [Mechanics] / L. D. Landau, E. M. Lifshic – 5-th edition – M.: Fizmatlit, 2004. – 224 P. [in Russian]
- Landau, L. D. Kvantovaja mehanika (nereljativitskaja teorija) [Quantum mechanics (nonrelativistic theory)] / L. D. Landau, E. M. Lifshic – 6-th edition – M.: Fizmatlit, 2004. – 800 P. [in Russian]
- Wigner E. P. On the quantum correction for thermodynamic equilibrium / E. P. Wigner // Physical Review – 1932. – Vol. 40 (5). – P. 749–759. doi:10.1103/PhysRev.40.749.
- Shljajh V.P. Kvantovaja optika v fazovom prostranstve [Quantum optics in phase space] / V.P. Shljajh – M.: Fizmatlit, 2005. – 760 P. [in Russian]
- Matveev A.N. Atomnaja fizika [Atomic physics] / A. N. Matveev – M.: Vyssh. shk., 1989. – 439 p. [in Russian]
- Web-service Bitbucket. – URL: https://bitbucket.org/iminchenko/oscillo/
