ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ЭЙЛЕРА ДЛЯ 2D ДВИЖЕНИЯ СЖИМАЕМОЙ СРЕДЫ
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ЭЙЛЕРА ДЛЯ 2D ДВИЖЕНИЯ СЖИМАЕМОЙ СРЕДЫ
Научная статья
Коптев А.В.1, *, Войтко И.В.2
1 ORCID: 0000-0003-2736-7585,
1, 2 Государственный университет морского и речного флота имени адмирала С. О. Макарова, Санкт-Петербург, Россия
* Корреспондирующий автор (alex.koptev[at]mail.ru)
Аннотация
Рассматриваются уравнения Эйлера для 2D неустановившегося движения сжимаемой среды, когда в качестве основных неизвестных выступают две компоненты вектора скорости, плотность и давление. Предложена процедура интегрирования, основанная на введении новых неизвестных и на общих положениях теории дифференциальных уравнений. В результате получены соотношения для простых алгебраических комбинаций основных неизвестных, удобные для решения гидромеханических задач и моделирования реальных потоков.
Ключевые слова: движение, идеальная сжимаемая среда, уравнения Эйлера, плотность, давление, псевдо-функция тока, интеграл.
INTEGRATION OF EULER EQUATIONS FOR 2D MOTION OF COMPRESSIBLE MEDIUM FLOW
Research article
Koptev A.V.1, *, Voytko I.V.2
1 ORCID: 0000-0003-2736-7585,
1, 2 Admiral Makarov state university of maritime and inland shipping, Saint-Petersburg, Russia
* Corresponding author (alex.koptev[at]mail.ru)
Abstract
The Euler equations for 2D unsteady motion of compressible medium flow are under consideration. Two components of velocity vector, density and pressure supposed as the main unknowns. We propose the procedure of integration which based on introduction of new variables and general statements of theory of partial differential equations. As the result we obtain ratios for simple algebraic combinations of main unknowns which convenient for solution of fluid mechanics problems and for simulation of real fluid and gaseous flow.
Keywords: motion, ideal compressible medium, Euler equations, density, pressure, stream pseudo function, integral.
Introduction
The Euler equations are one of the basic relations of classical hydromechanics. Equations of that type describe the motion of fluid and gaseous ideal media. Absence of internal friction is the main characteristic of such a media. Euler equations are of interest from a mathematical point of view as one of the types of nonlinear partial differential equations. These equations are of a great interest as well from practical point of view, as they are the basis for calculation of structures in energy engineering, shipbuilding, aircraft engineering, hydraulic engineering and other areas [1-4].
For the case of 2D isothermal motion of a compressible medium in the absence of external mass forces the Euler equations can be represented as
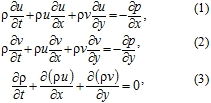
Two components of the velocity vector u, v, density ρ and pressure p represents the main unknowns. Each of these values is a function of Cartesian coordinates x, y and time t. The main problem is to find these functions.
For today there are no general approaches to the solution of a problem at hand [1],[5] and studies on this direction are very relevant. In the paper under consideration an attempt is made to integrate equations (1-3) based on the introduction of new unknowns and general provisions of the theory of partial differential equations [6]. A similar method was previously used by author for the purpose to integrate the Navier – Stokes equations [7-8].
The canonical form of equations
Despite the external differences, each of the equations (1-3) can be represented on a divergent form that is, as a linear combination of the first derivatives over x, y and t
![]()
Where ![]() are some combinations of main unknowns u, v, ρ, p.
are some combinations of main unknowns u, v, ρ, p.
Equation (3) already has the form (4) and does not need to be transformed. For this equation ![]()
Equations (1) and (2) can also be reduced to form (4) as a result of the following transformations. Consider the first nonlinear terms in the left-hand parts (1-2) and transform them using equation (3) as
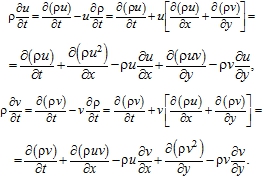
Using the representation data for ![]() and transferring all the terms to the left, we come to the equations of the form (4)
and transferring all the terms to the left, we come to the equations of the form (4)
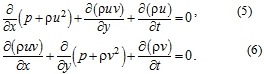
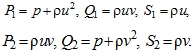
Thus, each of the equations (1-3) has a canonical representation (4).
Integration and further transformation
Each of the equations of the form (4) allows integration in the general form.
Indeed, the left part (4) represents the divergence of vector ![]() on 3D space-time coordinate system
on 3D space-time coordinate system ![]() . When using the well-known formula of vector analysis
. When using the well-known formula of vector analysis
![]()
we conclude that the general solution of (4) is determined by the coordinates of vector ![]() , where
, where ![]() is an arbitrary vector of space. Last statement is equally true when
is an arbitrary vector of space. Last statement is equally true when ![]() is a vector of space
is a vector of space ![]() when, as in our case, there is an arbitrary vector from space
when, as in our case, there is an arbitrary vector from space ![]() .
.
Specify the coordinates of vector and the result is equalities as the next
![]()
Where ![]() are arbitrary doubly differentiable functions of x, y, t, representing the coordinate functions of vector
are arbitrary doubly differentiable functions of x, y, t, representing the coordinate functions of vector ![]() .
.
For our case i=1, 2, 3 and therefore we have three triples of expressions similar to (8). These expressions are defined by nine double-differentiable functions of x, y, t.
For these functions, we introduce sequential numbering and notation ![]() , where k=1, 2,...,9. These functions are called as stream pseudo-functions of the first order with number k. First index in its designation corresponds to the number of the stream pseudo-function, and the second to its order. At this stage the order is equal to 1. Taking into account the previously obtained expressions for
, where k=1, 2,...,9. These functions are called as stream pseudo-functions of the first order with number k. First index in its designation corresponds to the number of the stream pseudo-function, and the second to its order. At this stage the order is equal to 1. Taking into account the previously obtained expressions for ![]() on the basis of (8) we come to the relations as the following
on the basis of (8) we come to the relations as the following
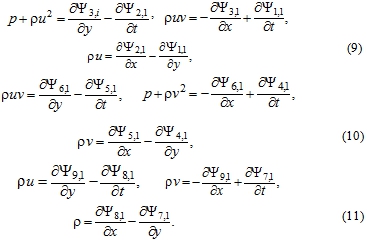
The nine equations of system (9-11) represent the primary expressions for the integral of the Euler equations, since the combination of their first derivatives leads to equations (5-6), (3). Whereas the last ones are equivalent to original Euler equations.
We set the task to simplify the equations (9-11) as much as possible and give them the most convenient form for practical use. We suggest the transformations as the following. Add up the first of (9) and the second of (10) and multiply the result on ![]() . We obtain a convenient expression for pressure as
. We obtain a convenient expression for pressure as
![]()
So, the unknown p is excluded according to (12) and instead of two equations, which contain p, we use equations (12) and (13).
We also pay attention to the following regularity characteristic of some equations of the system (9-11). Three pairs of equations with the same left-hand parts are distinguished. These equations are the second of (9) and the first of (10), the third of (9) and the first of (11), and the third of (10) and the second of (11). By calculating the soil differences for each pair, we arrive at three new equations that can be represented in canonical form (4)
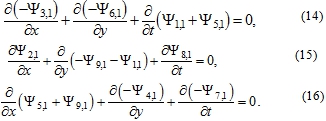
For each of equations (14-16), we find the solution in general form similar to the way it was done earlier for equations (5-6) and (3). In this case, three triples of new functions are introduced. These functions are called as stream pseudo-functions of the second order and designated as ![]() where j=1, 2,...,9. Note that second lower index in their designation is equal 2.
where j=1, 2,...,9. Note that second lower index in their designation is equal 2.
As a result, we obtain new equations as the next
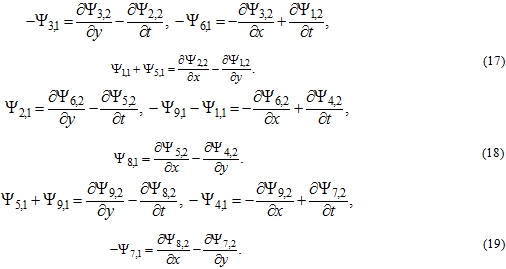
Of the nine equations (17-19) we define ![]() by first order derivatives of
by first order derivatives of ![]() . Substituting these expressions in equations of determining system we obtain significant simplifications.
. Substituting these expressions in equations of determining system we obtain significant simplifications.
Equations (14-16) are executed identically, and it means that the number of equations of the determining system has been reduced by three. So in defining system there are only six equations. These are equations (12), (13), the first and second of (9), the third of (10) and the third of (11). These equations are simplified and take the form of
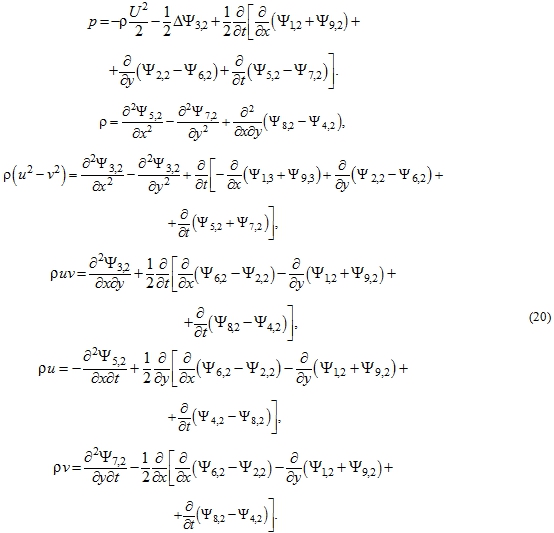
then how ![]() denotes the modulus of the velocity vector
denotes the modulus of the velocity vector ![]() .
.
Analysis of equations (20) leads to the conclusion that the right-hand sides are determined only by the following six stream pseudo-functions of the second order and their simple combinations:
![]()
Equations (20) can be given a more concise form, if you enter the notation of the formulas
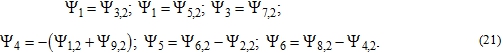
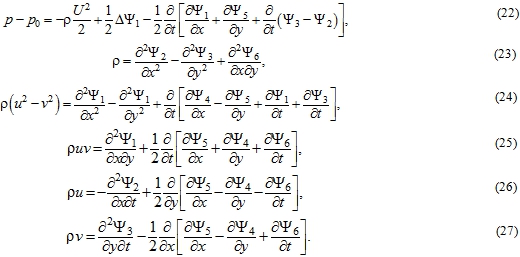
Conclusion
Equations (22-27) links main unknowns u, v, ρ, p and associated ones ![]() . The last appeared as a result of integration of the original equations. The order of derivatives of main unknowns in equations (22-27) is one less than their order in the original equations (1-3). In the original equations (1-3) the order of the derivatives of main unknowns is first then how in (22-27) the derivatives of main unknowns are absent. That is we can assume that the order of derivatives is zero. A direct test can be made that exist a combination of the first derivatives that converts equations (22-27) to (3),(5-6) or to the equivalent Euler equations (1-3).
. The last appeared as a result of integration of the original equations. The order of derivatives of main unknowns in equations (22-27) is one less than their order in the original equations (1-3). In the original equations (1-3) the order of the derivatives of main unknowns is first then how in (22-27) the derivatives of main unknowns are absent. That is we can assume that the order of derivatives is zero. A direct test can be made that exist a combination of the first derivatives that converts equations (22-27) to (3),(5-6) or to the equivalent Euler equations (1-3).
The equations (22-27) considered together represent the integral of Euler equations (1-3) for 2D unsteady motion of the compressible medium.
The main unknowns in equations (22-27) appear in the form of simple algebraic combinations, and there is an excess of the number of unknowns (ten) over the number of equations (six). The solution of equations (22-27) is a simpler mathematical problem than the solution of the original Euler equations (1-3). Equations (22-27) are more convenient for modeling real flows and more convenient for solving problems of fluid and gas mechanics.
In the particular case of motion of an incompressible medium when ![]() , solutions of some fluid mechanics problems presented in the works [9], [10], [11].
, solutions of some fluid mechanics problems presented in the works [9], [10], [11].
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Лойтцянский Л. Г. Механика жидкости и газа / Л. Г. Лойтцянский // М.: Наука. – 1987.
- Кармак T. Аэродинамика. Избранные главы в их историческом развитии / Т. Кармак // Ижевск: Регулярная и хаотическая динамика. – 2001.
- Лаврентьев M.А. Проблемы гидродинамики и их математические модели / М. А. Лаврентьев, Б. В. Шабат // М.: Наука. – 1973.
- Келдыш M. В. Избранные труды / М. В. Келдыш, С. А. Чаплыгин // М.: Наука. – 1976.
- Charles L. Fefferman. Existence and smoothness of the Navier – Stokes equations / C. L. Fefferman // Preprint, Princeton university, Math. Dept., Princeton, NJ, USA. – 2000. – P. 1-5.
- Степанов В. В. Курс дифференциальных уравнений / В. В. Степанов // М.: Едиториал УРСС. – 2004.
- Коптев А. В. Новый подход к исследованию трехмерных уравнений Навье – Стокса / А. В. Коптев // Саранск: Труды Средне-волжского математического общества, Т. 3–4, №1, 2001. – С. 281–287.
- Koptev A.V. Integrals of Motion of an Incompressible Medium Flow. From Classic to Modern / A. V. Koptev // Handbook in Navier–Stokes Equations: Theory and Applied Analysis. – Nova Sciences Publishers. Inc., NY, USA. – 2017, P. 443-459.
- Коптев А. В. Теоретическое исследование обтекания цилиндра потоком идеальной несжимаемой жидкости при наличии экранирующего эффекта / А. В. Коптев // Вестник государственного университета морского и речного флота им. адмирала С.О. Макарова. – 2 (36), 2016, С. 127-137.
- Koptev A. V. D’Alembert Paradox in Near Real Conditions / A. V. Koptev // Journal of Siberian federal university, Math. & Phys. – 2017. – 10(2). – P. 170-180.
- Коптев А. В. Невязкий аналог задачи Пуазейля / А. В. Коптев // Вестник Российского университета Дружбы Народов. Математика. Информатика. Физика. – Т. 26, №2, 2018, С. 140-154 .
Список литературы на английском языке / References in English
- Lojtcyanskij L. G. Mekhanika zhidkosti i gaza [Mechanics of fluid and gas ] / L. G. Lojtcyanskij // M.: Nauka. – 1987. [in Russian]
- Karmak T. Aehrodinamika. Izbrannye glavy v ih istoricheskom razvitii [Selected topics in their historical development] / T. Karmak // Izhevsk: Regulyarnaya i haoticheskaya dinamika [Regular and chaotic dynamics]. – 2001. [in Russian]
- Lavrent'ev M.A. Problemy gidrodinamiki i ih matematicheskie modeli [Problems of hydrodynamics and their mathematical models] / M. A. Lavrent'ev, B. V. SHabat // M.: Nauka. – 1973. [in Russian]
- Keldysh M. V. Izbrannye trudy [Selected papers] / M. V. Keldysh, S. A. CHaplygin // M.: Nauka. – 1976. [in Russian]
- Charles L. Fefferman. Existence and smoothness of the Navier – Stokes equations / C. L. Fefferman // Preprint, Princeton university, Math. Dept., Princeton, NJ, USA. – 2000. – P. 1-5.
- Stepanov V. V. Kurs differencial'nyh uravnenij [Сourse of differential equations] / V. V. Stepanov // M.: Editorial URSS. – 2004. [in Russian]
- Koptev A. V. Novyj podhod k issledovaniyu trekhmernyh uravnenij Nav'e – Stoksa [New approach to research of 3D Navier – Stokes equations ] / A. V. Koptev // Saransk: Trudy Sredne-volzhskogo matematicheskogo obshchestva, T. 3–4, №1, 2001. – S. 281–287. [in Russian]
- Koptev A.V. Integrals of Motion of an Incompressible Medium Flow. From Classic to Modern / A. V. Koptev // Handbook in Navier–Stokes Equations: Theory and Applied Analysis. – Nova Sciences Publishers. Inc., NY, USA. – 2017, P. 443-459.
- Koptev A. V. Teoreticheskoe issledovanie obtekaniya cilindra potokom ideal'noj neszhimaemoj zhidkosti pri nalichii ehkraniruyushchego ehffekta [Theoretical research of the flow around the cylinder of an ideal incompressible medium in the presence of a shielding effect ] / A. V. Koptev // Vestnik gosudarstvennogo universiteta morskogo i rechnogo flota im. admirala S.O. Makarova. – 2 (36), 2016, S. 127-137. [in Russian]
- Koptev A. V. D’Alembert Paradox in Near Real Conditions / A. V. Koptev // Journal of Siberian federal university, Math. & Phys. – 2017. – 10(2). – P. 170-180.
- Koptev A. V. Nevyazkij analog zadachi Puazejlya [An Inviscid analogue of the Poiseulle problem ] / A. V. Koptev // Vestnik Rossijskogo universiteta Druzhby Narodov. Matematika. Informatika. Fizika. – T. 26, №2, 2018, S. 140-154 . [in Russian]
