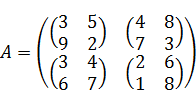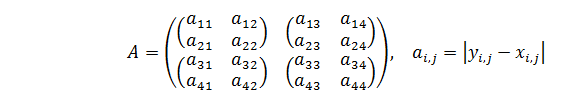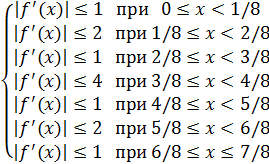ИГРЫ С КЛЕТОЧНЫМИ МАТРИЦАМИ КАК ИГРЫ ПРЕСЛЕДОВАНИЯ И УБЕГАНИЯ
Яксубаев К.Д.
Кандидат физико-математических наук, Астраханский государственный архитектурно-строительный университет
ИГРЫ С КЛЕТОЧНЫМИ МАТРИЦАМИ КАК ИГРЫ ПРЕСЛЕДОВАНИЯ И УБЕГАНИЯ
Аннотация
Для игр с клеточными матрицами применена методика Л.С. Понтрягина, что привело к разделению матричной игры на игру преследования и игру убегания.
С помощью двоичного кодирования графы траектории игроков были вложены в единичные отрезки системы координат. Это позволило визуализировать и описать причинные операторы преследования.
Приведена методика сведения дифференциальной игры к клеточной матричной игре.
Ключевые слова: клеточные матрицы, теория игр, цена игры.
Yaksubaev K.D.
PhD in Physics and Mathematics, Russian State Astrakhan University of Architecture and Building
GAME WITH CELLULAR MATRICES AS GAMES OF PURSUIT AND EVASION
Abstract
For games with the cell matrices the technique of L. S. Pontryagin, which led to the separation matrix games game of pursuit and evasion game.
Using the binary coding column the trajectories of the players were invested in isolated segments of the coordinate system. This allowed to visualize and describe causal operators persecution.
The technique of information differential games to cell matrix game
Keywords: cell matrix, game theory, price of the game.
Настоящая статья является продолжением работы автора [3]. Приведем краткое описание игры типа TG1212с клеточной матрицей в чистых стратегиях. На первом ходе игрок P выбирает строку, а игрок Q столбец фактор-матрицы. На втором ходе все повторяется. Первый игрок стремится максимизировать выигрыш, а второй игрок стремится минимизировать проигрыш.
Применение методики дифференциальных игр, разработанной Л.С. Понтрягиным к играм с клеточной матрицей.
Рассмотрим игру со следующей платежной клеточной матрицей:
Элементы платежной матрицей примем за расстояние между обоими игроками. Тогда игрок P будет у нас убегающим игроком, поскольку он хочет увеличить расстояние между игроками. А игрок Q будет догоняющим игроком.
Тогда в соответствии с методикой Л.С. Понтрягина эта игра распадается на две игры: игру преследования и игру убегания. Рассмотрим игру преследования.
Построение оператора преследования для игры преследования с помощью графа
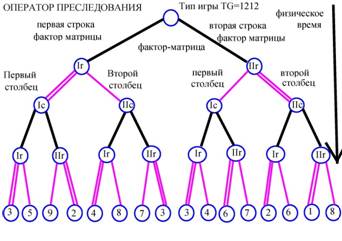
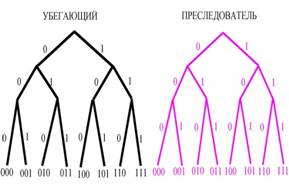
Тип игры TG= 1212 c точки зрения теории дифференциальных игр есть игра преследования. Решением такой игры является оператор преследования. Этот оператор на любой ход убегающего должен выдавать оптимальный ход преследователя и должен соблюдать принцип причинности. Он не должен знать будущего. Приведем изображение причинного оператора преследования на графе.
Мы видим на графе, что на любой ход черного игрока P, указан оптимальный ход розового игрока Q.
Сведение дифференциальной игры с фиксированным временем окончания игры к клеточной матричной игре
Рассмотрим дифференциальную игру с фиксированным временем окончания игры 
со следующими уравнениями движения:
.
Игрок 
называется убегающим игроком, а игрок 
преследователем.
Целевой функцией называется расстояние между игроками в момент времени , то есть
Сведем рассматриваемую дифференциальную игру к матричной игре следующим способом. Пусть управляющие параметры 
принимают всего два значения: 
Временной промежуток 
разобьём на два отрезка: 
. Конечно точность приближения сооруженной нами дискретной модели игры невелика. Но для демонстрации метода этого достаточно.
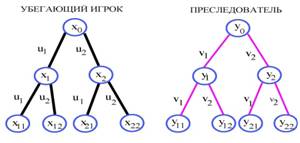
Траектории движения в выбранной нами дискретной модели при схематическом изображении будут таковыми:
Теперь можно составить клеточную матрицу игры:
Сведение дифференциальной игры с фиксированным временем окончания к клеточной игре позволяет нам использовать теорию дискретных игр [1;2].
Описание причинных операторов для игры с клеточными матрицами
Определение. Оператор 
называется причинным, если для любых двух функций, таких что 
на отрезке 
следует, что 
на том же отрезке, где 
.
Рассмотрим следующую игру на графах:
Траектории мы закодировали нулями и единицами. Введем следующее представление двоичных чисел.
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 0 | 1/8 | 2/8 | 3/8 | 4/8 | 5/8 | 6/8 | 7/8 |
Вложение графа траекторий убегающего игрока в плоскость
Вложение производится следующим образом:
Получим множество С1. Аналогично вложим граф траекторий догоняющего игрока в плоскость и получим множество С2. Будем предполагать, что оба множества есть подмножества пространства непрерывных функций С[0,1] с равномерной метрикой.
Вложение обоих графов в единичный отрезок
Каждую траекторию мы закодировали двоичным числом, и поэтому такое вложение возможно. Итак, один граф у нас располагается по оси иксов, а другой по оси игреков.
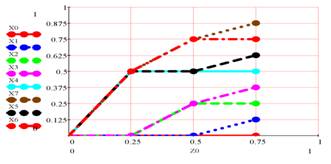
Визуализация отображения одного графа в другой.
Любая кусочно-линейная функция, с вершинами в указанных точках есть визуальный образ оператора, отображающего один граф в другой.
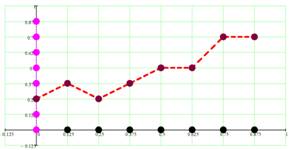
Остается отобрать из всей совокупности кусочно-линейных функций причинные операторы.
Теорема. Причинными функциями (операторами) являются те, и только те функции, производные которых удовлетворяют следующему условию:
Правильнее записать эти условия, через константы Липшица. Заметим, что цифры 1, 2, 4 это как раз и есть расстояния в равномерной норме во множестве С1 между нашими восьми функциями убегающего игрока. Если теперь мы индуцируем норму С на отрезок [0;1] по оси иксов, а на оси игреков все оставим по прежнему, то описание всех причинных операторов примет такой вид.
Теорема. Причинными операторами являются все не растягивающие функции, то есть все кусочно-линейные функции с константой Липшица равной единице.
Центральная задача дискретной теории игр. Описать все причинные операторы, отображающие один граф в другой с разного рода ограничениями.
К задаче визуализации причинных отображений одного счетного двоичного графа на другой
Уложим счетный двоичный граф убегающего игрока на единичный отрезок по оси иксов, а счетный двоичный граф преследователя на единичный отрезок по оси игреков. И любая функция, располагающаяся в единичном квадрате, есть отображение одного графа на другой.
Но можно ли, следуя приведенной выше методике, выделить из всех отображений класс причинных операторов неизвестно?
К проблеме аксиомы выбора
Аксиома выбора. Из многозначного отображения всегда можно выделить однозначную ветвь-селектор.
Аксиома выбора с принципом причинности должна звучать так.
Из многозначного причинного отображения всегда можно выделить однозначную причинную ветвь - селектор.
В работе автора [4] доказана следующая теорема.
Теорема. Из многозначного компактнозначного причинного отображения:
,
всегда можно выделить однозначный причинный селектор. Доказательство опирается на теорему Тихонова.
На взгляд автора, если эту теорему изложить в максимально абстрактной форме, с привлечением понятия порядковая непрерывность, то полученное обобщение может стать удачным заменителем аксиомы выбора. Конечно, если будет доказано, что оно слабее теоремы Тихонова.
Можно ли игру двух игроков на любом конечном графе реализовать как игру с клеточной матрицей?
Рассмотрим конечный граф, на котором играют поочередно два игрока. И пусть выигрышные очки стоят не только на концах графа, но и в различных вершинах. Полученные баллы оба игрока складывают.
Лемма. Все очки, складывая соответственным образом, можно спустить на концы графа.
Лемма. Игру двух игроков на любом конечном графе можно реализовать как игру с некоторой клеточной матрицей.
Доказательство. Пусть задан граф, на котором идет игра двух игроков.
По предыдущей лемме можно спустить все платежные числа на концы графа и там их сложить.
Пусть М это максимум, а m это минимум из всех чисел, расположенных на концах графа.
Будем достраивать граф фиктивными ребрами, двигаясь снизу вверх, по следующему принципу. Первому игроку, играющему на максимум, будем подсовывать самое маленькое число на конце фиктивного ребра при его фиктивном ходе. Для второго игрока будем подсовывать самое большое число.
Так двигаясь снизу вверх, можно будет достроить весь граф до красивого вида, который является графом некоторой клеточной матрицы. Цена игры при этом не изменится.
Пример, экономической задачи с клеточной матрицей с глубиной вложения пять.
| Товаропроизводитель игрок Q | ||||||
| Напитки | Молочные продукты | |||||
| Безалкогольные | Алкогольные | Творог | Молоко | |||
| Ситро | Квас | Вина | Водка | Сорт 1. Сорт 2. | Сорт 1. Сорт 2. | |
| Сорт 1. Сорт 2. | Сорт 1. Сорт 2. | Крепленные | Сухие | Сорт 1. Сорт 2. | ||
| Сорт 1. Сорт 2 Сорт 3. | Сорт 1. Сорт 2. | |||||
Нужно вводя фиктивные числа и ребра уровнять все ветви до глубины вложения пять. Затем, тоже проделать и для первого игрока. Оба графа перемножим и получим граф клеточной матрицы, с глубиной вложения пять.
На этом простом примере видно, что реальная экономическая игровая задача может иметь глубину и 10 и 20, и более 20.
Вся теория Нэша построена на одной матрице. Наши простые примеры
показывают, нереальность моделирования экономики одной матрицей, и необходимость движения от Нэша к Л.С. Понтрягину.
Литература
- Сатимов Н., Азамов А. Нелинейные дискретные игры убегания. Кибернетика.- Киев.1976. - №4.- С.79-74.
- Азамов А.А. Основания теории дискретных игр. Ташкент: Niso Poligraf, 2011.
- Яксубаев К.Д. Игры с клеточными матрицами // http://research-journal.org: Международный научно-исследовательский журнал. - 2016. doi: 10.18454/IRJ.2016.47.020
- Яксубаев К.Д. Выделение причинного селектора из многозначного отображения. Рукопись депонирована в ВИНИТИ, 1987. №620-В87. 18 с.
References
- Satimov N., Azamov A. Nelinejnye diskretnye igry ubeganija. Kibernetika.- Kiev.1976. - №4.- S.79-74.
- Azamov A.A. Osnovanija teorii diskretnyh igr. Tashkent: Niso Poligraf, 2011.
- Jaksubaev K.D. Igry s kletochnymi matricami // http://research-journal.org: Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. - 2016. doi: 10.18454/IRJ.2016.47.020
- Jaksubaev K.D. Vydelenie prichinnogo selektora iz mnogoznachnogo otobrazhenija. Rukopis' deponirovana v VINITI, 1987. №620-V87. 18 s.