ИДЕМПОТЕНТНАЯ МОДЕЛЬ КЛАССИЧЕСКОЙ ЗАДАЧИ О НАЗНАЧЕНИЯХ

Черных О.О.

Соискатель, Липецкий государственный технический университет

ИДЕМПОТЕНТНАЯ МОДЕЛЬ КЛАССИЧЕСКОЙ ЗАДАЧИ О НАЗНАЧЕНИЯХ

Работа поддержана РФФИ, проект № 11-07-00580-а

Аннотация В статье рассматриваются основной принцип идемпотентной алгебры, приводится краткое обсуждение преимуществ идемпотентного подхода. В работе приводится идемпотентная модель постановки задачи о назначениях, которая позволяет привести задачу к линейному виду даже в нелинейном случае.

Ключевые слова: идемпотентная алгебра, идемпотентная арифметика, тропическая алгебра, задача о назначениях.

Chernykh O.O.

Applicant, Lipetsk State Technical Univeristy

IDEMPOTENT MODEL OF THE CLASSICAL ASSIGNMENT PROBLEM

Abstract The main principle of idempotent algebra is observed in this article, the main advantages of idempotent approach are given. An idempotent model of a classical assignment problem is given, this model makes even non-linear assignment problems become linear ones.

Key words: idempotent algebra, idempotent arithmetic, tropical algebra, assignment problem.

Стремительно развивающимся разделом математики является идемпотентная алгебра, или как ее еще называют – тропическая алгебра. Такое «экзотическое» название полностью соответствует «необычности» идемпотентного подхода. Представим математику, в которой операция сложения обладает свойством идемпотентности, то есть: x + x = x. Несмотря на кажущуюся непривычность, ничего необычного в таком определении нет: типичные идемпотентные операции – операции взятия минимума или максимума. Идемпотентная арифметика базируется на двух операциях: модифицированное сложение – взятие максимума – и модифицированное умножение – сложение в привычном понимании. Поэтому идемпотентную алгебру часто называют и «макс- плюс» алгеброй.

В основании идемпотентной алгебры лежит понятие идемпотентного полукольца – множества M , на котором определены две бинарные ассоциативные операции ⊕ и ⊗, обладающие нейтральными относительно этих операций элементами 0 и 1, при этом вторая операция связана с первой законом дистрибутивности слева и справа:

a ⊗ (b ⊕ c) = a ⊗ b ⊕ a ⊗ c,

(b ⊕ c) ⊗ a = b ⊗ a ⊕ c ⊗ a

но, самое главное, как мы отметили выше, операция ⊕ обладает свойством идемпотентности, т. е.

a ⊕ a = a    ∀a ∈ M

Затронув название «макс-плюс» алгебры нужно сразу оговориться, что операции сложения и максимума отнюдь не единственные операции в идемпотентной арифметике. Известно несколько идемпотентных алгебр:

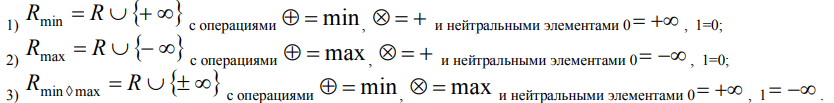В чем же преимущества идемпотентного подхода? Наиболее полезным свойством идемпотентных алгебр для моделирования динамических систем является тот факт, что динамику систем можно описать линейными (над соответствующей идемпотентной алгеброй) уравнениями. Так, многие классические задачи оптимизации сводятся в терминах идемпотентной математики к решению обобщенных линейных уравнений[1-3]. Кроме того, модели стохастических систем также могут быть описаны с использованием векторных понятий идемпотентной алгебры.

В нашей стране существуют целые школы, занимающиеся как теоретическими аспектами идемпотентных алгебр [3], так и более прикладными [2]

В работе [4] автором был дан краткий критический анализ возможности применимости идемпотентного подхода при решении экономико-математических задач, таких как: сетевое планирование, планирование производства, задача моделирования СМО.

Одной из важных задач ЭМММ является задача о назначениях – частный случай транспортной задачи. Пусть имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами.

Составим идемпотентную модель для данной задачи.

Исходными данными для задачи являются:

n - количество ресурсов;

m - количество работ;

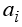- некоторая доля ресурса A_i , причем i = 1,...n;                                                                                                 

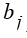- некоторая доля работы (задания)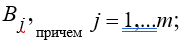 

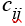- некоторая стоимость выполнения задания 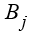с помощью ресурса Ai .  

Необходимо определить порядок распределения заданий по ресурсам, описываемый с помощью фиктивной переменной 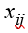 принимающей значения:

Причем целевая функция L(x) стремится к минимуму. Тогда идемпотентная модель задачи может быть записана в виде:

   

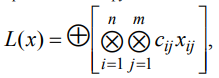
с ограничениями:

 

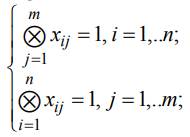
где 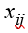 - факт назначения работы ресурсу.

В идемпотентом полукольце 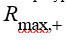 даже в нелинейной постановке задача сводится к линейному виду, что облегчает ее решение и вычисления.