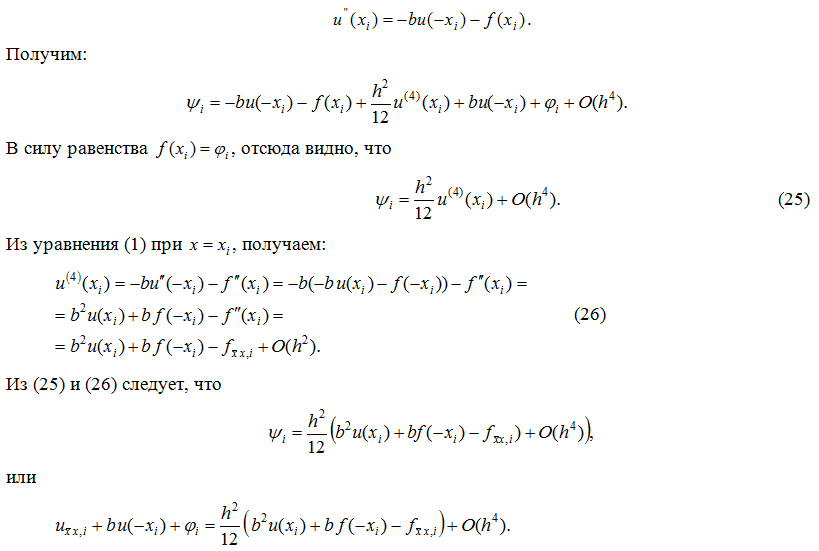ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ПЕРВОГО РОДА ДЛЯ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ НА СИММЕТРИЧНОМ ОТРЕЗКЕ
Абрегов М.Х.1, Канчукоев В.З.1, Шарданова М.А.2
1кандидат физико-математических наук, 2 аспирант, ФГБОУ ВПО «Кабардино-Балкарский Государственный Университет им. Х.М. Бербекова»
ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ПЕРВОГО РОДА ДЛЯ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ НА СИММЕТРИЧНОМ ОТРЕЗКЕ
Аннотация
В работе разработан численный метод решения первой краевой задачи для модельного обыкновенного дифференциального уравнения второго порядка с отклоняющимся аргументом. Построена конечно-разностная схема, аппроксимирующая дифференциальную задачу с точностью второго порядка по шагу равномерной сетки. Из полученной априорной оценки решения конечно-разностной схемы следует ее сходимость при определенных условиях на входные параметры задачи. Предложен метод реализации конечно-разностной схемы, состоящий в представлении ее решения в виде суммы двух сеточных функций, каждая из которых является решением классической краевой задачи для разностного уравнения второго порядка. Проведенные вычислительные эксперименты подтверждают полученные в работе теоретические результаты. В работе приведен пример задачи, имеющей бесчисленное множество решений вследствие нарушения условия ее однозначной разрешимости.
Ключевые слова: уравнение с отклоняющимся аргументом, численный метод решения, двухточечная краевая задача, симметричный отрезок, конечно-разностная схема, априорная оценка, сходимость.
Abregov M.H.1, Kanchukoev V.Z.1, Shardanova М.А.2
1 PhD in Physics and Mathematics, 2 Postgraduate student, Kabardino-Balkaria State University named after H.M. Berbekov
NUMERICAL METHODS FOR SOLVING BOUNDARY VALUE PROBLEMS FOR LINEAR FIRST KIND SECOND ORDER DIFFERENTIAL EQUATIONS WITH DEVIATING ARGUMENT ON BALANCED SEGMENT
Abstract
In the developed numerical method for solving the first boundary value problem for a model second-order ordinary differential equation with deviating argument. Built finite-difference scheme that approximates the differential problem with the accuracy of second order in step a uniform grid. From the resulting a priori estimates of the solution finite difference scheme implies its convergence under certain conditions to the input parameters of the problem. The method of implementation of the finite scheme consisting in the presentation of its solutions in the form of a sum of two grid functions, each of which is a solution of the classical boundary value problem for a differential equation of second order. Conducted computing experiments confirm the theoretical results obtained in this work. The work is an example of the problem, which has countless solutions due to violations of the conditions for its unique solvability.
Keywords: equation with deviating argument, numerical solution method, two-point boundary value problem, symmetric interval, finite-difference scheme, a priori estimate, convergence.
Литература
- Лесев В.Н., Шарданова М.А. Краевая задача для дифференциального уравнения с отклоняющимся аргументом.// Современные проблемы науки и образования. – 2015. - №2 (часть 2).
- Мудров А.В. О связи систем обыкновенных дифференциальных уравнений и уравнений с запаздывающим аргументом.// Вестник Новосибирского государственного университета. Серия: Математика, механика, информатика.- 2007.-Т.7,-№2,-С. 52-64.
- Норкин С.Б. Дифференциальные уравнения второго порядка с запаздывающим аргументом.// Москва. Наука, 1965,-356 с.
- Прасолов А.В. Динамические модели с запаздыванием и их приложения в экономики и инженерии.// Санкт-Петербург.-2010,-289 с.
- 5. Самарский А.А. Теория разностных схем,// Москва. Наука, 1989,-616 с.
- Шхануков М.Х. О сходимости конечноразностной схемы. // Вычислительная математика и математическая физика, 1969, - Т.9 С. 712-714.
References
- Lesev V.N., Shardanova M.A. Kraevaya zadacha dlya differencialnogo uravnenia s otclonyaushimsia argumentum.// Sovremenie problemi nauki i obrazovania.– 2015. - №2 (часть 2).
- Mudrov A.B. О svyazi system obiknovennih differencialnih uravnenii i uravnenii s zapazdivaushim argumentom.// Vestnik Novosibirskogo gosudarstvennogo universiteta. Seria: Matematica, mehanika, informatica. - 2007.-Т.7,-№2,-С. 52-64.
- Norkin С.B. Differencialnie uravnenia vtorogo poradka s zapazdivausim argumentom.// Mockva, Nauka, 1965,-356 с.
- Prasolov A.V. Dinamicheskie modeli s zapazdivaniem I ih prilogenia v economici i ingeneri. // Sankt- Peterburg.-2010,-289 с.
- Samarski A.A. Teoria raznostnih shem.// Moskva. Nauka,1989,-616 с.
- Shanukov M.H. O shodimosti konechnoraznostnoi shemi.// Vichislitelnaya matematika I matematicheskaya phisika,1969, - Т.9 С. 712-714.