АВТОМОДЕЛЬНОСТЬ ЗАДАЧИ ТЕПЛОВОЙ КОНВЕКЦИИ, ОСРЕДНЕННОЙ ПО ТОНКОМУ СЛОЮ
Сахарова Л.В.
Доктор физико-математических наук, Ростовский государственный экономический университет
АВТОМОДЕЛЬНОСТЬ ЗАДАЧИ ТЕПЛОВОЙ КОНВЕКЦИИ, ОСРЕДНЕННОЙ ПО ТОНКОМУ СЛОЮ
Аннотация
Получена экспоненциальная автомодельная замена для задачи тепловой конвекции, осредненной по тонкому слою испаряющейся жидкости. Задача является моделью высыхания невязкой, нетемпературопроводной протяженной капли. Задача сведена к системе обыкновенных дифференциальных уравнений, получено ее автомодельное решение. Решение соответствует испарению- конденсации пленки жидкости в условиях дренажа линии трехфазного контакта.
Ключевые слова: Математическая модель, автомодельные решения, капля, испарение-конденсация.
Sakharova L.V.
PhD in Physics and Mathematics, Rostov State University of Economics
SIMILAR PROBLEM OF THERMAL CONVECTION, AVERAGED OVER A THIN LAYER
Abstract
We obtain exponential self-similar replacement for the problem of thermal convection, averaged over a thin layer of the evaporating liquid. The problem is a model of dry non-viscous, netemperaturoprovodnoy extended drop. The problem is reduced to a system of ordinary differential equations, obtained its self-similar solution. The solution complies ispareniyu- liquid film condensation in a drain three-phase contact line
Keywords: mathematical model, similar solutions, drop, evaporation- condensation.





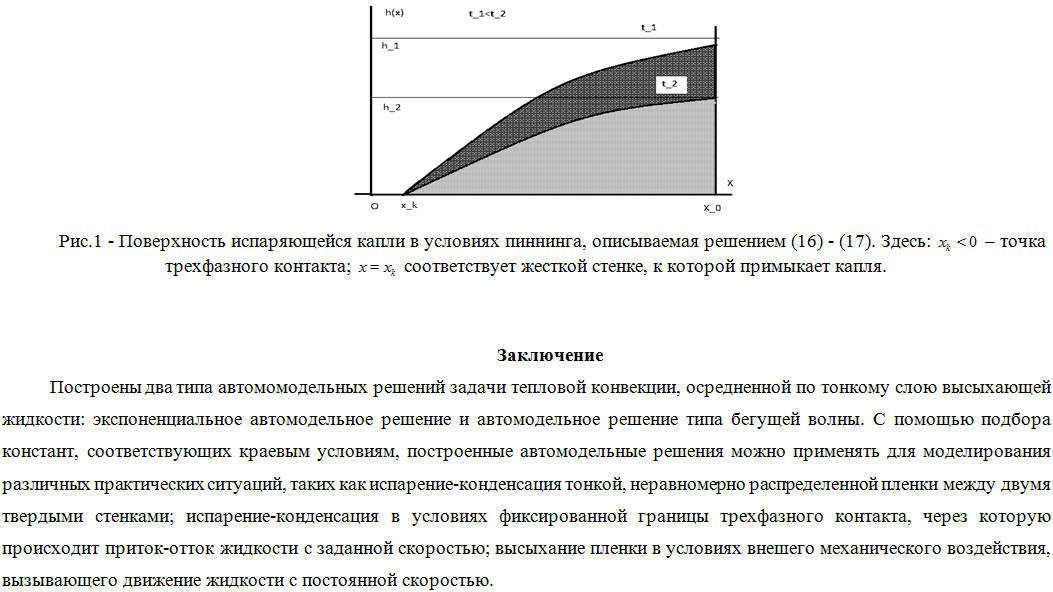
Литература
- Рапис Е. Белок и жизнь (самосборка и симметрия наноструктур белка). Иерусалим; М.: ЗЛ. Милта-ПКП ГИТ, 2002. 257 с. ионарной и нестационарной математических моделей течений в испаряющейся капле. Компьютерные исследования и моделирование. 2012 Т. 4 № 4 С. 811-825.
- Ющенко А.А., Даудова А.Д., Аюпова А.К., Урляпова Н.Г., Шатохина С.Н. Способы оценки общетоксического действия лекарственных средств на организм. Пат. РФ 2232387. 2004. Б.И. № 17.
- Takhistov P., Chang H. Complex Stain Morphologies // Industrial and Engineering Chemistry Research. 2002. Vol. 41, no. 25. P. 6256-6269.
- Tarasevich Y. Y., Vodolazskaya I.V., Sakharova L.V. Mathematical modeling of pattern formation caused by drying of colloidal film under a mask. Eur. Phys. J. E (2016) 39: 26 DOI 10.1140/epje/i2016-16026-5.
- Bhardwaj R., Longtin J.P., Attinger D. A numerical investigation on the influence of liquid properties and interfacial heat transfer during microdroplet deposition onto a glass substrate. International Journal of Heat and Mass Transfer 50 (2007) 2912-2923. P. 2912 - 2923.
- Maki K. L., Kumar S. Fast Evaporation of Spreading Droplets of Colloidal Suspensions // Langmuir. 2011. Vol. 27, no. 18. P. 11347- 11363.
- Жуков М.Ю., Ширяева Е.В., Полякова Н.М.Моделирование испарение капли жидкости: монография. Южный федеральный университет. - Ростов-на-Дону: Издательство Южного федерального университета, 2015 - 208 с.
References
- Rapis E. Belok i zhizn' (samosborka i simmetriya nanostruktur belka). Ierusalim; M.: ZL. Milta-PKP GIT, 2002. 257 s. ionarnoj i nestatsionarnoj matematicheskikh modelej techenij v isparyayushhejsya kaple. Komp'yuternye issledovaniya i modelirovanie. 2012 T. 4 № 4 S. 811-825.
- YUshhenko А.А., Daudova А.D., Аyupova А.K., Urlyapova N.G., SHatokhina S.N. Sposoby otsenki obshhetoksicheskogo dejstviya lekarstvennykh sredstv na organizm. Pat. RF 2232387. 2004. B.I. № 17.
- Takhistov P., Chang H. Complex Stain Morphologies // Industrial and Engineering Chemistry Research. 2002. Vol. 41, no. 25. P. 6256-6269.
- Tarasevich Y. Y., Vodolazskaya I.V., Sakharova L.V. Mathematical modeling of pattern formation caused by drying of colloidal film under a mask. Eur. Phys. J. E (2016) 39: 26 DOI 10.1140/epje/i2016-16026-5.
- Bhardwaj R., Longtin J.P., Attinger D. A numerical investigation on the influence of liquid properties and interfacial heat transfer during microdroplet deposition onto a glass substrate. International Journal of Heat and Mass Transfer 50 (2007) 2912-2923. P. 2912 - 2923.
- Maki K. L., Kumar S. Fast Evaporation of Spreading Droplets of Colloidal Suspensions // Langmuir. 2011. Vol. 27, no. 18. P. 11347- 11363.
- ZHukov M.YU., SHiryaeva E.V., Polyakova N.M.Modelirovanie isparenie kapli zhidkosti: monografiya. YUzhnyj federal'nyj universitet. - Rostov-na-Donu: Izdatel'stvo YUzhnogo federal'nogo universiteta, 2015 - 208 s.
