АППРОКСИМАЦИЯ И ИНТЕРПОЛЯЦИЯ ВОЛНОВЫХ СИГНАЛОВ В БАЗИСЕ ОКАЙМЛЯЮЩИХ ФУНКЦИЙ ПРИ ИССЛЕДОВАНИИ МЕХАНИЧЕСКИХ И ИНЫХ ФИЗИЧЕСКИХ ПОЛЕЙ
АППРОКСИМАЦИЯ И ИНТЕРПОЛЯЦИЯ ВОЛНОВЫХ СИГНАЛОВ В БАЗИСЕ ОКАЙМЛЯЮЩИХ ФУНКЦИЙ ПРИ ИССЛЕДОВАНИИ МЕХАНИЧЕСКИХ И ИНЫХ ФИЗИЧЕСКИХ ПОЛЕЙ
Научная статья
Седов А.В. * ORCID: 0000-0001-7515-3886, Федеральный исследовательский центр Южный научный центр Российской академии наук, Ростов на Дону, Россия; Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова, Новочеркасск, Россия
* Корреспондирующий автор (sedov07[at]list.ru)
Аннотация Предложена формула тригонометрической аппроксимации и интерполяции сигналов на основе базиса окаймляющих функций, упрощающая процесс моделирования и восстановления волновых изменений сигналов по измеренным отсчетам. Предложены модификации формулы для одновременной параллельной фильтрации сигналов на основе применения семейств новых окаймляюще-фильтрующих функций. Показаны преимущества применения предложенного подхода и формул перед известными. Показана взаимосвязь формулы с известной теоремой отсчетов. Ключевые слова: тригонометрическая аппроксимация, окаймляющие функции, параллельная фильтрация, теорема отсчетов, волновые сигналы.APPROXIMATION AND INTERPOLATION OF WAVE SIGNALS IN THE BASIS OF BORDERING FUNCTIONS IN THE STUDY OF MECHANICAL AND OTHER PHYSICAL FIELDS
Research article
Sedov A.V. *
ORCID: 0000-0001-7515-3886, Federal Research Center Southern Scientific Center of the Russian Academy of Sciences, Rostov-on-Don, Russia; M.I. Platov South-Russian State Polytechnic University, Novocherkassk, Russia * Corresponding author (sedov07[at]list.ru)
Abstract A formula for trigonometric approximation and interpolation of signals based on the bordering functions is proposed, which simplifies the process of modeling and reconstructing changes of wave signals from measured samples. Proposed modifications of the formula for simultaneous parallel filtering of signals based on the use of families of new bordering and filtering functions. The advantages of using the proposed approach and formulas over the known ones are shown. The interrelation of the formula with the known sampling theorem of is shown. Keywords: trigonometric approximation, bordering functions, parallel filtering, sampling theorem, wave signals.
На разных этапах регистрации и моделирования сигналов волновых и резонансных изменений механических и физических полей используют преобразования сигналов к частотам дискретизации, отличным от используемых при измерении. Решение последней задачи осуществляют на основе интерполяции (аппроксимации) сигналов с преобразованием исходного сигнала, измеренного с частотой дискретизации w1 в идентичный ему сигнал с более высокой частотой дискретизации w2 .При этом задаются требуемым отношением частот L = w1/w2 или коэффициентом интерполяции. К существующим подходам решения указанной задачи относят интерполяцию сигналов с использованием:
- цифровых фильтров с конечной импульсной характеристикой (КИХ) и полифазных структур на основе этих фильтров;
- интерполирующих полиномов Лагранжа, Чебышева, Лежандра, тригонометрических полиномов различного вида, а также иных систем ортогональных базисных функций;
- статистических подходов и моделей;
- базисных функций Котельникова-Шеннона, ядер Дирихле и предлагаемых в [1, С.54] [2, С. 47] окаймляющих функций.
Кратко охарактеризуем перечисленные подходы. Нерекурсивные, симметричные цифровые фильтры с КИХ, описываются передаточной функцией вида
![]() где x (z), xи(z) – z-изображения преобразованного входного x[kT/L], k = 0,1,2,... и xи[kT/L], k = 0,1,2,... сигналов фильтра;
где x (z), xи(z) – z-изображения преобразованного входного x[kT/L], k = 0,1,2,... и xи[kT/L], k = 0,1,2,... сигналов фильтра; ![]() – коэффициенты фильтра низкой частоты, обеспечивающие частоту среза π/T рад/c; – порядок фильтра. Перед использованием фильтра исходный входной сигнал x[kT], k = 0,1,2,... добавляя между его отсчетами по L - 1 нулевому отсчету. Это обстоятельство делает невозможным использование фильтров с КИХ в случае дробного значения L. Кроме того, цифровой фильтр не обеспечивают точного восстановления непрерывного сигнала по дискретным отсчетам или точной интерполяции сигнала, даже в случае выполнения условий теоремы дискретизации Котельникова, из-за не идеальности амплитудно- и фазо-частотных характеристик получаемого фильтра. Использование полифазных структур на основе переключающихся фильтров с КИХ также не решает перечисленных проблем.
Полиномы Лагранжа, Чебышева, Лежандра и другие, а также иные системы ортогональных базисных функций иногда применяются при интерполяции дискретных сигналов, особенно в случае нерегулярной дискретизации и восстановления сигналов. Однако если выбор частоты дискретизации сигналов осуществляют на основе теоремы дискретизации, что связано с гармоническим (частотным) представлением сигналов, использование полиномов для восстановления таких сигналов не вполне логично и в общем случае не обеспечивает точного его восстановления даже при выполнении указанной теоремы. Правомерно и адекватно применение в этом случае тригонометрических полиномов различного вида, в частности, представления в форме ряда Фурье.
Возможны статистические подходы и модели при интерполяции дискретных сигналов, в частности, модели случайных импульсных потоков, однако они применимы только при достаточном статистическом материале о сигнале, позволяющем использовать теорию вероятностей, теорию случайных функций, математическую статистику.
При детерминированной постановке задачи интерполяции наиболее соответствующими условиям теоремы дискретизации являются формулы, построенные на основе базисных функций Котельникова-Шеннона, ядер Дирихле и описываемых окаймляющих функций.
Исследования показали, что лучший результат при интерполяции конечного во времени сигнала x(t) с ограниченным спектром по измеренным равномерным отсчетам
– коэффициенты фильтра низкой частоты, обеспечивающие частоту среза π/T рад/c; – порядок фильтра. Перед использованием фильтра исходный входной сигнал x[kT], k = 0,1,2,... добавляя между его отсчетами по L - 1 нулевому отсчету. Это обстоятельство делает невозможным использование фильтров с КИХ в случае дробного значения L. Кроме того, цифровой фильтр не обеспечивают точного восстановления непрерывного сигнала по дискретным отсчетам или точной интерполяции сигнала, даже в случае выполнения условий теоремы дискретизации Котельникова, из-за не идеальности амплитудно- и фазо-частотных характеристик получаемого фильтра. Использование полифазных структур на основе переключающихся фильтров с КИХ также не решает перечисленных проблем.
Полиномы Лагранжа, Чебышева, Лежандра и другие, а также иные системы ортогональных базисных функций иногда применяются при интерполяции дискретных сигналов, особенно в случае нерегулярной дискретизации и восстановления сигналов. Однако если выбор частоты дискретизации сигналов осуществляют на основе теоремы дискретизации, что связано с гармоническим (частотным) представлением сигналов, использование полиномов для восстановления таких сигналов не вполне логично и в общем случае не обеспечивает точного его восстановления даже при выполнении указанной теоремы. Правомерно и адекватно применение в этом случае тригонометрических полиномов различного вида, в частности, представления в форме ряда Фурье.
Возможны статистические подходы и модели при интерполяции дискретных сигналов, в частности, модели случайных импульсных потоков, однако они применимы только при достаточном статистическом материале о сигнале, позволяющем использовать теорию вероятностей, теорию случайных функций, математическую статистику.
При детерминированной постановке задачи интерполяции наиболее соответствующими условиям теоремы дискретизации являются формулы, построенные на основе базисных функций Котельникова-Шеннона, ядер Дирихле и описываемых окаймляющих функций.
Исследования показали, что лучший результат при интерполяции конечного во времени сигнала x(t) с ограниченным спектром по измеренным равномерным отсчетам ![]() дает использование окаймляющих функций
дает использование окаймляющих функций ![]() , предложенных в [1, С.54] [2, С. 47]. Формула интерполяции в этом случае имеет вид
, предложенных в [1, С.54] [2, С. 47]. Формула интерполяции в этом случае имеет вид
![]()
Основными преимуществами формулы (1) является:
- получение гладкого неразрывного интерполируемого сигнала xint (t) без точек неопределенностей значений (разрывов);
- тригонометрическое представление окаймляющих функций
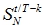 определяет согласованность с условиями теоремы дискретизации;
определяет согласованность с условиями теоремы дискретизации; - возможность быстрой вычислительной реализации интерполяции сигналов без предварительного вычисления спектра или коэффициентов разложения сигнала; подобно интерполирующему полиному Лагранжа, позволяющему осуществлять интерполяцию без предварительного вычисления коэффициентов, непосредственно «по узлам», но только в тригонометрическом базисе.
Выражение (1) условно можно рассматривать, как описывающее цифровой восстанавливающий фильтр не рекурсивного типа. Импульсная характеристика этого фильтра при этом совпадает с окаймляющей функцией ![]() , а амплитудно-частотная характеристика (АЧХ) такого фильтра соответствует АЧХ идеального восстанавливающего фильтра низкой частоты. Это подтверждает, что (1) осуществляет абсолютно точное восстановление (интерполяцию) конечного сигнала по дискретным отсчетам, если они были выбраны в соответствии с условиями теоремы отсчетов Котельникова-Шеннона. В случае не полного выполнения этого условия (наличие не нулевых высокочастотных составляющих выше частоты дискретизации пополам ws/2 формула реализует аппроксимацию сигнала.
Предлагается модификация выражения (1) вида
, а амплитудно-частотная характеристика (АЧХ) такого фильтра соответствует АЧХ идеального восстанавливающего фильтра низкой частоты. Это подтверждает, что (1) осуществляет абсолютно точное восстановление (интерполяцию) конечного сигнала по дискретным отсчетам, если они были выбраны в соответствии с условиями теоремы отсчетов Котельникова-Шеннона. В случае не полного выполнения этого условия (наличие не нулевых высокочастотных составляющих выше частоты дискретизации пополам ws/2 формула реализует аппроксимацию сигнала.
Предлагается модификация выражения (1) вида
![]()
![]() позволяющая помимо точной интерполяции (аппроксимации) осуществлять одновременно фильтрацию сигнала
позволяющая помимо точной интерполяции (аппроксимации) осуществлять одновременно фильтрацию сигнала ![]() , т.е. исключение из сигнала шумовых частотных составляющих. При этом в формуле ƒ1 и ƒ2 – относительные частоты среза фильтра задающие полосу пропускания фильтра (2) из полного частотного диапазона [0,0.5] или [0, ws/2];
, т.е. исключение из сигнала шумовых частотных составляющих. При этом в формуле ƒ1 и ƒ2 – относительные частоты среза фильтра задающие полосу пропускания фильтра (2) из полного частотного диапазона [0,0.5] или [0, ws/2]; ![]() ( ƒ1, ƒ2 ) – окаймляюще-фильтрующая функция первого рода.
Фильтрацию сигнала, осуществляемую с помощью выражения (2), назовем одновременной параллельной фильтрацией, т.к. при фильтрации используются одновременно все отсчеты сигнала отрезка наблюдения [0, Tc].
Выражение (2) определяет полосовой фильтр с полосой пропускания [f1, f2], однако небольшая ее модификация позволяет реализовать многополосные фильтры по формуле вида
( ƒ1, ƒ2 ) – окаймляюще-фильтрующая функция первого рода.
Фильтрацию сигнала, осуществляемую с помощью выражения (2), назовем одновременной параллельной фильтрацией, т.к. при фильтрации используются одновременно все отсчеты сигнала отрезка наблюдения [0, Tc].
Выражение (2) определяет полосовой фильтр с полосой пропускания [f1, f2], однако небольшая ее модификация позволяет реализовать многополосные фильтры по формуле вида
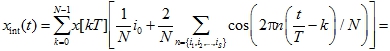
(3)
![]()
где ![]()
![]() – окаймляюще-фильтрующая функция второго рода.
– окаймляюще-фильтрующая функция второго рода.
Индексы ![]() определяют номера гармоник, которые должны оставаться в фильтрованном и интерполированном сигнале. Эти индексы выбираются из диапазона номеров гармоник присутствующих в сигнале
определяют номера гармоник, которые должны оставаться в фильтрованном и интерполированном сигнале. Эти индексы выбираются из диапазона номеров гармоник присутствующих в сигнале ![]() Индекс
Индекс ![]() определяет необходимо ли уничтожить или оставить в сигнале постоянную составляющую. Каждый из индексов
определяет необходимо ли уничтожить или оставить в сигнале постоянную составляющую. Каждый из индексов ![]() определяет присутствие в спектре функции
определяет присутствие в спектре функции![]()
![]() , той или иной частотной составляющей с амплитудой равной единице.
Использование окаймляющих функций позволяет по новому сформулировать теорему отсчетов Котельникова-Шеннона для конечного сигнала x(t) с ограниченным спектром, заданным равноотстоящими отсчетами
, той или иной частотной составляющей с амплитудой равной единице.
Использование окаймляющих функций позволяет по новому сформулировать теорему отсчетов Котельникова-Шеннона для конечного сигнала x(t) с ограниченным спектром, заданным равноотстоящими отсчетами ![]() . В отличие от известной теоремы отсчетов [3, С. 405] [4, С. 160] [5, С. 232] [6, С. 320] [7, С. 260], сформулированной только для бесконечного во времени сигнала x(t) и использующей формулу интерполяции на основе ядра Котельникова-Шеннона (sinc-функции), предложенная формула (1) использующая окаймляющие функции
. В отличие от известной теоремы отсчетов [3, С. 405] [4, С. 160] [5, С. 232] [6, С. 320] [7, С. 260], сформулированной только для бесконечного во времени сигнала x(t) и использующей формулу интерполяции на основе ядра Котельникова-Шеннона (sinc-функции), предложенная формула (1) использующая окаймляющие функции ![]() расширена и на случай интерполяции конечного во времени сигнала.
Более того, не сложно показать, что sinc-функция (ядро Котельникова-Шеннона) является частным предельным случаем предложенной окаймляющей функции
расширена и на случай интерполяции конечного во времени сигнала.
Более того, не сложно показать, что sinc-функция (ядро Котельникова-Шеннона) является частным предельным случаем предложенной окаймляющей функции ![]() при N → ∞ [8, С. 323].
Теорема отсчетов (для конечного во времени сигнала и равно отстоящих отсчетов). Конечный во времени непрерывный сигнал x(t), рассматриваемый на интервале наблюдения t∈[0, Tc). как период бесконечного сигнала x(t) со спектром ограниченным полосой частот [0,ƒв] может быть точно восстановлен по формуле (1) на основе равноотстоящих дискретных значений x[kT], k=0,...,N-1 интервала наблюдения Tc=NT, выбранных с интервалом дискретизации T < 1/(2ƒв) и с использованием окаймляющих базисных функций
при N → ∞ [8, С. 323].
Теорема отсчетов (для конечного во времени сигнала и равно отстоящих отсчетов). Конечный во времени непрерывный сигнал x(t), рассматриваемый на интервале наблюдения t∈[0, Tc). как период бесконечного сигнала x(t) со спектром ограниченным полосой частот [0,ƒв] может быть точно восстановлен по формуле (1) на основе равноотстоящих дискретных значений x[kT], k=0,...,N-1 интервала наблюдения Tc=NT, выбранных с интервалом дискретизации T < 1/(2ƒв) и с использованием окаймляющих базисных функций ![]() .
Из предельной взаимосвязи sinc-функций и окаймляющих функций можно сделать вывод, что и общеизвестная теорема Котельникова-Шеннона [9, С. 402] [10, С. 130] [11, С. 253] может рассматриваться как частный случай при N → ∞ сформулированной выше теоремы отсчетов для конечного во времени сигнала.
.
Из предельной взаимосвязи sinc-функций и окаймляющих функций можно сделать вывод, что и общеизвестная теорема Котельникова-Шеннона [9, С. 402] [10, С. 130] [11, С. 253] может рассматриваться как частный случай при N → ∞ сформулированной выше теоремы отсчетов для конечного во времени сигнала.
| Финансирование Работа выполнена в рамках реализации Государственного задания Южного научного центра РАН, проект 0256-2018-0003, № госрегистрации 01201354242 и гранта РФФИ 18-08-01012. | Funding The work was performed within the framework of the State assignment implementation of the Southern Scientific Center of the Russian Academy of Sciences, project 0256-2018-0003, state registration number 01201354242 and RFBR grant 18-08-01012. |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Седов А. В. Уточнение теоремы дискретизации и формулы восстановления сигнала по дискретным отсчетам / А.В. Седов // Известия вузов. Электромеханика. – 2001. – № 2. – С.52-59.
- Седов А. В. Интерполяция и фильтрация сигналов в многоскоростных микропроцессорных системах моделирования, контроля и управления. / А. В. Седов // Известия вузов. Электромеханика. – 2003. – № 4. – С. 45-50.
- Shannon C. E. A Mathematical Theory of Communication / C .E. Shannon // The Bell System Technical Journal. – 1948. – July, October. – Vol. 27. – P. 379–423, 623–656.
- Горелов Г. В. Нерегулярная дискретизация сигналов / Г. В. Горелов – М.: Радио и связь, 1982. – 255 с.
- Трахтман А. М. Введение в обобщенную спектральную теорию сигналов / А. М. Трахтман – М.: Советское Радио, 1972. – 352 с.
- Smith S. W. The Scientist and Engineer's Guide to Digital Signal Processing / S. W. Smith – California Technical Publishing, 1997 – 630 р.
- Носач В. В. Решение задач аппроксимации с помощью персональных компьютеров / В. В. Носач – М.: МИКАП, 1994. – 382 с.
- Седов А. В. Моделирование объектов с дискретно-распределенными параметрами: декомпозиционный подход / А.В. Седов – М.: Наука, 2010. – 438 с.
- Shannon C. E. A mathematical theory of communication. / C. E. Shannon // Bell System Tech. J. – 1948. – № 27. – P. 379-423.
- Котельников В. А. О пропускной особенности «эфира» и проволоки в электросвязи / В. А. Котельников // Матер. к I Всесоюзн. съезду по вопросу реконструкции дела связи. – Изд. ред. упр. связи РККА, 1933.– C.128-133.
- Whittaker J. M. Interpolatory Function Theory / J. M. Whittaker –Cambridge Univ. Press, Cambridge, 1935. – 320 p.
