КВАНТОВОРАЗМЕРНАЯ МАТЕРИЯ
Научная статья
Жуков Н.Д.*
ООО «НПП Волга», Саратов, Россия
* Корреспондирующий автор (ndzhukov[at]rambler.ru)
АннотацияВ статье сформулировано понятие квантоворазмерной материи как материальной среды, состоящей из элементов, в которых квазисвободные электроны движутся в условиях размерного квантования энергии и импульса в глубокой протяжённой потенциальной яме. Известные современной науке свойства неорганических кристаллических квантоворазмерных частиц предложено применить к элементам «живой» материи, в частности, молекуле ДНК. Предположено, что ДНК присущи волновые свойства и специфическое электромагнитное излучение, позволяя клеткам совершать информационный обмен и обуславливая возможность оперирования информацией сложного порядка. В качестве средства измерений параметров излучения предложено использовать микроструктуры с квантоворазмерными полупроводниковыми частицами, для создания которых требуются исследования и отработка технологий при вариациях составов, форм, наноразмеров, наноразмещений.
Ключевые слова: размерное квантование, глубокая протяжённая квантовая яма, квантоворазмерная частица, квантовая структура, волна де Бройля, туннельный электронный транспорт, квантовый осциллятор, инфракрасное излучение, терагерцевое излучение, информационный процесс.
QUANTUM-DIMENSIONAL MATTER
Research article
Zhukov N.D.*
NPP Volga LLC, Saratov, Russia
* Corresponding author (ndzhukov[at]rambler.ru)
AbstractThe article formulates the concept of quantum-dimensional matter as a material medium consisting of elements in which quasi-free electrons move under the conditions of dimensional quantization of energy and momentum in a deep extended potential well. The properties of inorganic crystalline quantum-sized particles known to modern science are proposed to be applied to the elements of "living" matter, in particular, the DNA molecule. It is assumed that DNA has wave properties and specific electromagnetic radiation allowing cells to exchange information and making it possible to operate with information of a complex order. As a means of measuring radiation parameters, it is proposed to use microstructures with quantum-sized semiconductor particles, the creation of which requires research and development of technologies with variations in compositions, shapes, nanoscale sizes, and nanoschemes.
Keywords: dimensional quantization, deep extended quantum well, quantum-dimensional particle, quantum structure, de Broglie wave, tunneling electron transport, quantum oscillator, infrared radiation, terahertz radiation, information process.
ВведениеОпределение материи расширялось с развитием различных областей науки. В доквантовое время материальные объекты можно было описать классическими свойствами – масса, температура, делимость и т. п. С развитием электродинамики, а затем теории относительности и квантовой механики это понятие дополнилось его связями с гравитацией и волнами [1].
Вещество в классическом понимании состоит из фермионов (для случая данного рассмотрения – электронов, протонов, нейтронов), доминирующих, как форма материи, в Солнечной и ближайших звёздных системах [1]. Свойства веществ зависят от состава и движения фермионов в широком смысле этих слов.
Состояние и свойства веществ определяются внутренними размерными параметрами и временными процессами, обусловленными квантуемым движением фермионов. Квантование происходит по определяющим параметрам движения – энергии Ẽ и волнового вектора k, связанного с вектором импульса квантовым соотношением p=hk (h – постоянная Планка) – и состоит в том, что их значения принимают дискретный ряд, определяемый структурой и свойствами вещества, например, кристалла.
В конкретном смысле состояние вещества всегда ограничено размерами. Открытие в 17-м веке микроскопа (Леонардо да Винчи, Левенгук) и его развитие в 18-м веке (Кулибин, Ломоносов) [2] позволило различить микронные размеры и, тем самым, начать эпоху микрометрии, завершившуюся в 20-м веке фундаментальным направлением – микроэлектроникой.
К концу 20-го века на размерной шкале материальных объектов были «перекрыты» практически все интервалы, кроме области наноразмеров. Однако, еще в начале XX века немецкий биохимик В. Оствальд опубликовал книгу «Мир обойденных величин», в которой шла речь о новой в то время области химии — коллоидной химии, которая и имела дело именно с частицами нанометровых размеров (хотя тогда еще этот термин не употреблялся). Уже тогда он отмечал, что дробление материи в какой-то момент приводит к новым свойствам, что от размера частицы зависят свойства и всего материала [3].
Первое упоминание методов, которые впоследствии будут названы нанотехнологией, многие источники связывают с выступлением Р. Фейнмана «Внизу полным-полно места», сделанным им в 1959 году в Калифорнийском технологическом институте, где он предположил о возможности механического манипулирования одиночными атомами. В 1981 г. Г. Бинниг и Г. Рорер создали сканирующий туннельный микроскоп, что дало возможность не только получать изображения отдельных атомов, но и манипулировать ими [4]. Впервые термин «нанотехнология» употребил Норио Танигути в 1974 году. Он назвал этим термином производство изделий нанометровых размеров [5]. В начале 21-го века чётко сформировались понятия нанотехнологии [6, 7], нанонауки [8], наноиндустрии [9].
За 20 последних лет 20-го века, однако, существенных достижений не произошло ни в нанотехнологии, ни в нанонауке. Первые же 20 лет 21-го века стали прорывными для нанотехнологии, начиная с национальной нанотехнологической инициативы (NNI) США. Первое десятилетие, однако, не увенчалось существенными результатами [10]. За 20 же лет, в целом, произошли огромные перемены в информационной части – опубликовано около 100 тысяч научных статей и получено более 10 тысяч патентов [11]. В 2020 году издано более 50 монографий на темы наноматериалов, наноструктур и их применений. Практические же результаты, в основном, связаны с созданием и развитием производств пассивных (нанокомпоненты, нанопорошки, нанокомпозиты) и относительно простых активных (светодиоды, лазеры, микроэлектроника, биосенсоры) наноструктур. Сложные активные наноструктуры (молекулярные, модульные, интеллектуальные наносистемы) находятся в начале пути своего развития [11].
Современные практические нанотехнологические результаты получены на наноструктурах с размерностью 10 – 100 нм. Последующее развитие связано с освоением технологий наноструктур квантовой размерности – менее 10 нм. Решаемые при этом проблемы связаны с управлением составом, формой, размерами, способами синтеза и интегрирования квантоворазмерных элементов [12], [13], [14], [15].
Квантоворазмерные свойства и явления Движение квантовой частицы массы m в потенциальном поле V(r,t) четырёхмерного пространства описывается уравнением Шредингера, которое в нерелятивистском случае и координатно-векторном представлении имеет вид [16]: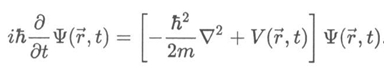 (1)
(1)
Решением уравнения Шредингера является волновая функция Ψ(r,t), интеграл от произведения квадрата модуля которой на параметр состояния определяет вероятность нахождения квантовой частицы в этом состоянии. Решение уравнения Шредингера в общем случае является сложной физико-математической задачей, решаемой, как правило, при принимаемых упрощениях.
В данной статье рассматриваются электронные свойства материальных структур, определяющие огромный спектр физических явлений и приборных свойств. При этом исследуется определяющая задача движения электрона в периодическом потенциальном поле конденсированной среды, когда становятся возможными ряд существенно упрощающих ограничений – атомы решётки неподвижны (адиабатическое приближение), многоэлектронная задача сводится к одноэлектронной (метод Хартри-Фока), волновая функция в объёмном кристалле представляется в виде суперпозиции отдельных атомных (метод Гайтлера-Лондона-Гайзенберга) и др. [17].
Для подавляющего числа случаев рассматриваются установившиеся во времени (стационарные) процессы. В этих случаях левая часть уравнения (1) равна нулю, а его решение относительно Ψ(r) выглядит как периодическая функция. При этом энергия электрона, вычисляемая как собственное значение волновой функции Ψ, в самом простом случае кубической формы квантоворазмерной частицы с ребром куба a, выражается в аналитическом виде [18]: Ẽglp = h2(8ma2)-1(g2 +l2 + p2), где: g, l, p = 1,2,3,…– квантовые числа, тройные совокупности которых соответствуют номерам квантованных уровней.
Волна́ де Бро́йля [19] — волна, определяющая плотность вероятности обнаружения нерелятивистской квантовой частицы в заданной точке конфигурационного пространства. В соответствии с принятой терминологией говорят, что волны де Бройля связаны с любыми квантовыми частицами и отражают их волновую природу. Длина волны де Бройля квантовой частицы определяется формулой Λ=h/p, из которой можно получить её выражение через кинетическую энергию и массу частицы:
| Λ= h(2mẼ)-1/2 | (2) |
Исходя из вышеизложенного, можно определить квантовый размер а материальной частицы и условие квантовой размерности по соотношению величин а и Λ.
Математический формализм решения уравнения Шредингера позволяет сформулировать ряд важных свойств квантовых частиц в квантовой материальной среде, занимающей ограниченную область пространства [16].
Решение уравнения Шредингера существует только для счётного множества значений энергии Ẽn и представляет собой счётное квантовыми числами n множество волновых функций Ψn, создающих общее решение как аддитивную суперпозицию элементов множества. Для одномерного движения квантовой частицы волновая функция Ψn дискретного спектра Ẽn, обращается в ноль (при конечных значениях координаты х) n раз (осцилляционная теорема).
Эти свойства позволяют упростить задачу их исследования, сведя её к частному одномерному линейному случаю дистанции х0 и прямоугольного потенциала V0. Тогда уравнение (1) примет простую легко решаемую форму:
| h2(8π2m)-1(d2Ψ/dx2) = V0Ψ 2 | (3) |
| Ψn = 8mV0(h2n2)-1sin(nx/x0) | (4) |
| En ~ h2n2(8mx02)-1 | (5) |
Исходя из всего вышеизложенного, можно заключить, что в рассматриваемой квантовой среде происходит отбор устойчивых состояний квантовой частицы (электрона) так, чтобы на линейной дистанции её движения укладывалось целое число полуволн. При этом устойчивым является состояние минимальной энергии, определяемое квантовым числом n=1. Всякие воздействия на квантовую частицу приводят к выводу из этого в другое адекватно устойчивое состояние. Устойчивость состояния движущейся квантовой частицы (электрона) в глубокой потенциальной яме и её стоячая волновая функция могут означать, что её движение имеет резонансный характер.
Здесь, таким образом, рассмотрен случай одиночной одномерной потенциальной прямоугольной ямы для электрона. На самом деле, в яме может быть много атомов, составляющих некую последовательность своих потенциалов на дистанции движения электрона. Понятно, что эти потенциалы будут создавать возмущение-препятствие движению электрона, а его иное устойчивое состояние возникнет в случае их закономерно регулярного (периодического) расположения. Как принято в физике твёрдого тела, в этом случае можно ввести понятие эффективной массы электрона, чтобы рассматривать его как квазисвободную квантовую частицу в протяжённой глубокой потенциальной яме.
Таким образом, квантоворазмерную материальную среду мы рассматриваем состоящей из некоторого числа дискретных квантоворазмерных частиц (QP), каждая из которых имеет закономерно-регулярное объёмное строение составных элементов (атомов и молекул), и в которой движение электрона происходит при закономерном отборе волнового процесса и электронных состояний по энергии и волновому вектору. Благодаря этому отбору, движение электрона можно рассматривать как состоящее из аддитивной совокупности линейных резонансных движений в закономерных направлениях QP.
Квантоворазмерные материальные структуры
К настоящему времени квантоворазмерные структуры – quantum dimensional structure (QDS) – хорошо классифицированы: нульмерные – квантовые точки (QD); одномерные – квантовые нити; двумерные – квантоворазмерные слои, плёнки, ленты; трёхмерные – квантоворазмерные частицы (QP) [12], [13].
Как передовой край науки и техники в последние годы развиваются различные варианты квантоворазмерных конфигуративных структур, например, графенов, для целей наноэлектроники [14].
Наибольшее развитие за последние несколько десятилетий получили технологии и применение квантоворазмерных слоёв в светодиодах и гетеролазерах, создавших гигантский поворот в науке, технике, быту.
В последние 10 лет активно исследуются коллоидные квантовые точки, и успешно освоены люминофоры на их основе. Сейчас в интернете они иллюстрируются, как общее достижение науки и техники [20] – рисунок 1 демонстрирует весь спектр видимого света, полученный на одном типе QD при вариации только их размера. Хорошо известно, что получение квантоворазмерных светодиодных гетероструктур на каждый узкий спектральный интервал – большая технологическая проблема, обусловленная использованием разных полупроводников и технологий, подходящих для каждого случая. Например, за синие гетероструктурные светодиоды (рис. 1, 2) в 2014 году была присуждена Нобелевская премия.

Рис. 1 – Люминофоры на коллоидных квантовых точках перекрывают весь спектр видимого света

Рис. 2 – Нобелевский светодиод
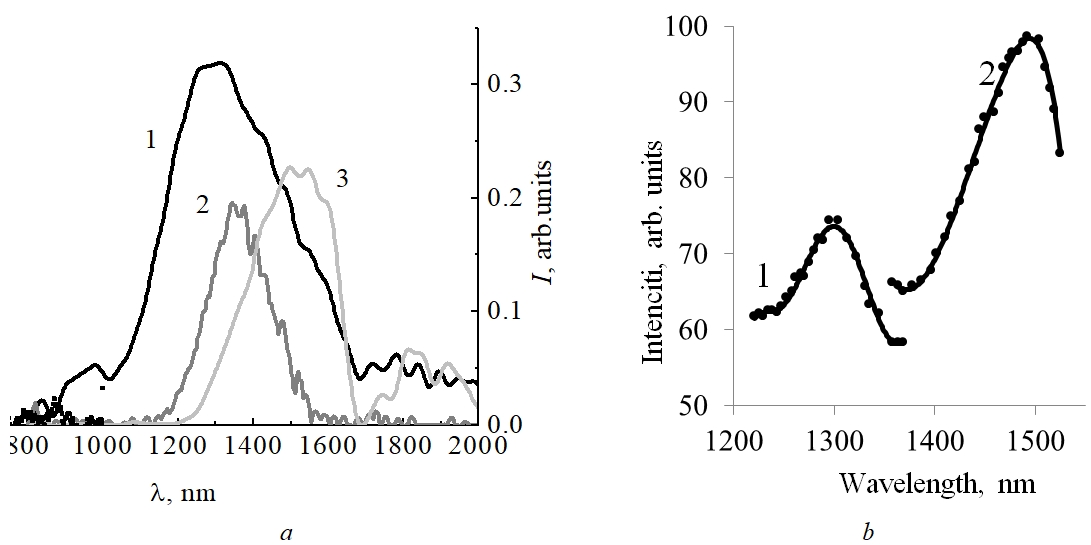
На рис. 3 приведены наши данные по инфракрасной фотолюминесценции на коллоидных квантовых точках узкозонных полупроводников [21].
Следующий исследуемый и технологически осваиваемый спектральный интервал излучений – инфракрасный длинноволновый и терагерцевый, о чём в следующем разделе.
Рис. 3 – Спектры инфракрасной фотолюминесценции:
a – QD-PbS/CdS (1,2,3); b – QD-InSb без оболочки (1) и с оболочкой CdS (2)
Осцилляции и волныВажнейшей спецификой прохождения электрона проводимости через квантоворазмерную частицу является проявление квазипериодических осцилляций коэффициента прохождения при изменении его энергии [18]. Экспериментально это выражается в пульсациях (осцилляциях) тока. При этом осцилляции проявляются как при внутрибарьерном (Ẽn<V0, финитное движение), так и надбарьерном (Ẽn>V0, инфинитное движение) прохождении. Физически это можно трактовать, как результат интерференции волн де Бройля, отражённых от скачков потенциала на границах потенциальной ямы, и то, что на её геометрической ширине укладывается целое число полуволн. Размерное квантование энергии и импульса электрона проявляется как отбор состояний резонансного движения электрона и стоячих волн де Бройля. Математически это выражается как результат решения уравнения Шредингера (в простейшем, но наглядном случае) в виде формулы (5). Частота пульсаций считается из формулы ν ~ En/h~ hn2(8md~2)-1 и значится в терагерцевом диапазоне.
При финитном движении электрона в QP теоретически возможны блоховские осцилляции [22]. При этом известно, что основным препятствием для их наблюдения и практических применений является их малое время жизни, обусловленное рассеянием электронов на дефектах кристаллической решётки и фононах. В квантоворазмерной частице с размерами а≤Λ электрон движется баллистически и резонансно, как бы, не реагируя на структурные помехи. Кроме того, путь движения электрона в структуре трёхмерной QP «выбирается» квантовым отбором. Эти обстоятельства могут свидетельствовать о реальной возможности действия осцилляций в QP при протекании тока или каких-то других энергетических воздействий на электрон. При этом электрон имеет свойства квантового осциллятора, то есть может проявлять электромагнитную волну.
Мы использовали вариант эмиссионно-инжекционного механизма возбуждения в мультизёренной микроструктуре, описанный в наших работах [15], [23]. Под действием приложенного к микроструктуре поля электрон претерпевает эмиссию из той или иной QP в нанозазор, а затем – инжекцию в соседнюю QP, в которой он термализуется, переходя в равновесное состояние. Мы предполагаем, что в этом процессе должна излучиться «лишняя» энергия в виде квантов hν = Ɛi ≈ (m/m0)-1ai-2. Например, при a=5 nm длина волны излучения должна быть ~20 μm – для QP-InSb. В связи с этим, интересно было получить излучение в длинноволновом диапазоне, для чего использованы QP-InSb с относительно большими размерами, синтезированные и исследованные нами в работе [24].
В случае, если предложенная нами микроструктура излучает, то, на основе принципа взаимности, она должна на это же излучение и реагировать, то есть быть адекватным фоторегистратором. Нами были проведены соответствующие эксперименты.
Экспериментально были взяты два одинаковых образца QP-InSb, изготовленных по методу, описанному в нашей работе [15], из которых один выполнял роль излучателя, а второй – приёмника. На излучатель подавали постоянное питающее напряжение V=, а на приёмнике – измеряли вольтамперные характеристики (ВАХ) методом, описанным в работе [15]. Было обеспечено и проверено отсутствие нежелательного (электрического и ёмкостного) взаимодействия образцов с гарантией того, что влияние одного на другой могло происходить только благодаря электромагнитному излучению. Была проведена оценка влияния тепловой радиации за счёт нагрева излучателя и установлено, что оно, в нашем случае пренебрежимо мало.
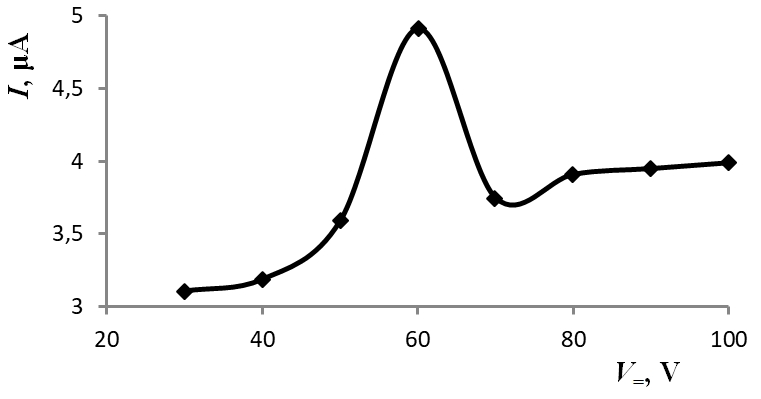
Наблюдались заметное повышение тока приёмника при повышении питающего напряжения V= на излучателе с 30 до 100 V и всплеск тока при напряжении V= = 60 V (рис 3). Этот выброс тока приёмника мы объясняем увеличением интенсивности излучения за счёт возможного энергетического перехода квантового осциллятора с нулевой энергии Ɛ0 (n=0) на первый резонансный уровень (n=1). По формуле энергии квантового осциллятора [25] Ɛ=Ɛ0(n + 1/2) интенсивность излучения, в нашем случае – тока приёмника, должна вырасти примерно в 1.5 раза, что и наблюдается по рис. 4 – отношение величин тока для случаев V= = 60 и V= = 30 равно ~5:3.
Рис. 4 – Зависимость тока приёмника при V=50 V от напряжения V= на излучателе
«Живая» материя
Живая материя, так же как и неживая, имеет размерное дробление. При этом базовой является биоклетка – элементарная единица строения, функционирования, размножения и развития всех живых организмов [26]. Всего в теле взрослого человека насчитывается около 230 различных типов клеток. Несмотря, однако, на многообразие форм, организация клеток всех живых организмов подчинена единым структурным принципам. Размеры клеток колеблются от единиц до десятков микрон. Клетки состоят из малых и больших молекул, выполняющих самые разные функции.
Дезоксирибонуклеи́новая кислота́ (ДНК) — макромолекула (одна из трёх основных, две другие — РНК и белки), обеспечивающая хранение, передачу из поколения в поколение и реализацию генетической программы развития и функционирования живых организмов [27].
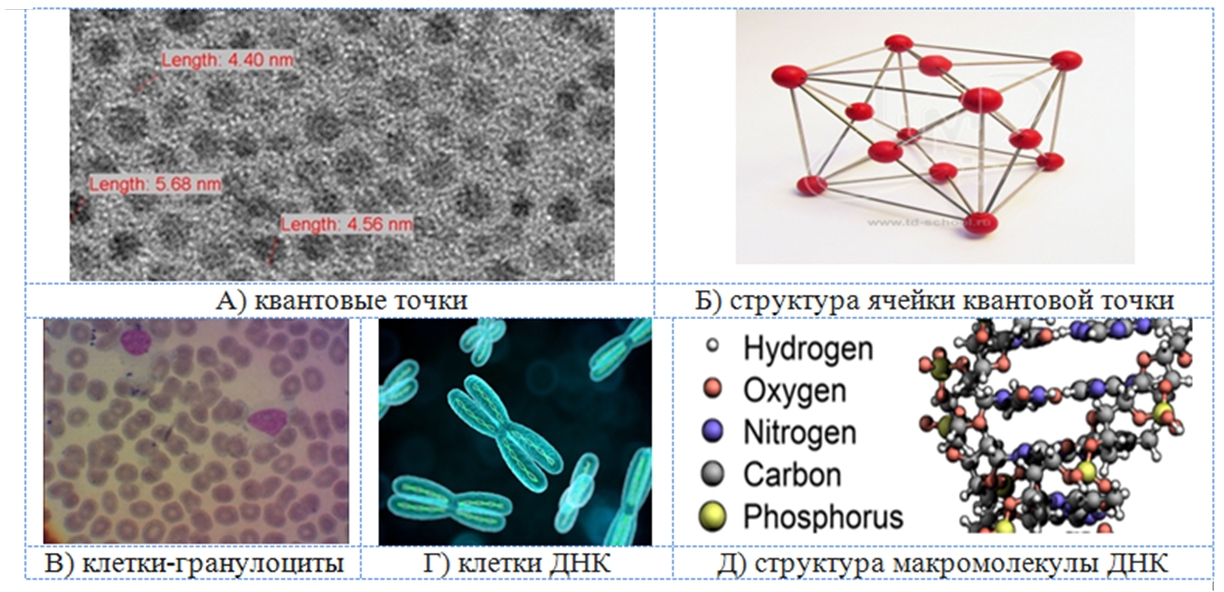
На рисунке 5 представлены ТЕМ-снимки и структурные схемы наиболее типичных наночастиц «живой» и, для сравнения, «неживой» материи, взятые из разных интернет-источников. Принципиально, наночастицы схожи по форме и размерам и отличаются сильно своей структурой – у «живой» она значительно сложнее.
Рис. 5 – Снимки в просвечивающем электронном микроскопе и структуры разных наночастиц
На рисунке 6 приведена структурная картина пространственного представления ДНК [28]. Полимерная молекула состоит из двух скрученных нитей-спиралей, соединённых поперечными связями из, примерно, 20 атомов каждая, и состоящих из мономерных звеньев – нуклеотидов.
Диаметр цилиндра, объемлющего двойную спираль, примерно, 2-3 нм, расстояние между соседними парами нуклеотидов вдоль спирали – 0,34 нм. Полный оборот двойная спираль делает через 10 пар. Длина нити-молекулы зависит от того, какому организму ДНК принадлежит: простейшим вирусам – несколько тысяч звеньев, бактериям – несколько миллионов, а высшим – миллиарды. Длина вытянутой молекулы – около двух метров. Но главная «причуда» заключена в том, что эта гигантская молекула «уложена» в одной клетке-частице размером не более десятков микрон.
Рис. 6 – Структурная картина представления ДНК [28]
С позиции нанонауки ДНК представляет собой длинную квантовую нить, состоящую из элементов – квантовых точек (нуклеотидов), связанных короткими (2-3 нм) квантовыми нитями. Понятно, что во всех этих элементах происходит квантоворазмерное движение электронов. Мы предполагаем, что в этих элементах электроны находятся как в глубоких потенциальных ямах и двигаются прямолинейно и резонансно, так, как было описано выше в случаях неорганических веществ. В этом случае электроны действуют как квантовые осцилляторы, излучая и поглощая электромагнитные волны.
Вычисления, подобные тем, что были проведены выше для квантоворазмерной частицы по формуле hν = Ɛi ≈ (m/m0)-1ai-2, приводят к значениям длины волны порядка 15 мкм (дальне-инфракрасный диапазон). На самом деле, для протяжённой квантовой нити геометрический размер резонансного движения электрона может быть равен длине волны де Бройля для электрона и превышать размер её поперечника. Тогда значения длины волны электромагнитных волн будут более рассчитанных 15 мкм и войдут в терагерцевый диапазон.
ЗаключениеИдея данной статьи заключается в том, чтобы сформулировать понятие квантоворазмерной материи, как среды, состоящей из квантоворазмерных электронных элементов живой и неживой природы, и предложить способ измерения информационных параметров наиболее важной для жизни биомолекулы – ДНК.
В основе такого способа может быть физическое явление линейного резонансного движения электрона в глубокой протяжённой квантоворазмерной потенциальной яме, приводящее к квантовой осцилляции электромагнитного излучения длинноволнового (дальнеинфракрасного и терагерцевого) спектрального диапазона. Мы предполагаем, что волновые свойства, присущие ДНК, позволяют клеткам совершать информационный обмен на уровне электромагнитных сигналов, обуславливая возможность оперирования информацией сложного порядка. Это излучение отличается от среднеинфракрасного теплового и люминесцентного сверхвысокой спектральной избирательностью, частичной или полной поляризацией и сверхмалым энергетическим уровнем. Доказательство существования и измерение такого излучения является непростой научно-технической задачей, возможность решения которой, однако, лежит на пути использования принципа обратимости явлений излучения и его регистрации в одинаковой физической структуре.
Техническое осуществление такой регистрирующей структуры лежит на пути создания реальной приборной микроструктуры из квантоворазмерных полупроводниковых частиц абсолютно одинаковых состава, формы, размеров и их закономерного наноструктурного расположения. Решение этой задачи потребует широкой вариации состава квантоворазмерных частиц, соответствующей отработки технологий их изготовления и структуры-носителя для них, методов самоорганизации приемлемого расположения наночастиц в приборной структуре.
Решение задачи, однако, позволит получать важную генетическую информацию и развивать методы генной аналитики и инженерии.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Материя // Вики – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki/ Материя(физика) (дата обращения 17.09.2021)
- История микроскопа // 4 глаза – [Электронный ресурс] – URL: https://4glaza-irkutsk.ru/ stati/kratkaya-istoriya-mikroskopa (дата обращения 17.09.2021)
- Мир обойдённых величин // Андронум – [Электронный ресурс] – URL: https: //andronum.com/product/ostvald-v-mir-oboydennyh-velichin/ (дата обращения 17.09.2021)
- Нанотехнология // Вики – [Электронный ресурс] – URL: https://ru.wikipedia. org/wiki/Нанотехнология (дата обращения 17.09.2021)
- Танигути_Норио // Вики – [Электронный ресурс] – URL: https://ru.wikipedia. org/wiki/Танигути_Норио (дата обращения 17.09.2021)
- Наноматериал // Вики – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki/Наноматериал (дата обращения 17.09.2021)
- Нанотехнология // Нефтегаз – [Электронный ресурс] – URL: https://neftegaz.ru/tech-library/tekhnologii/141844-nanotekhnologii/Нанотехнология (дата обращения 17.09.2021)
- Нанонаука // Вики – [Электронный ресурс] – URL: https://ru.wiktionary.org/wiki/Нанонаука (дата обращения 17.09.2021)
- Глухова О.Е. Основы наноиндустрии / Глухова О.Е., Гороховский А.В., Жуков Н.Д. и др. – Саратов: Изд-во Сара ун-та, 2009. – 384 с. ISBN 978-5-292-03982-2.
- Lok C. Nanotechnology: Small wonders / C. Lok // Nature 467, 18 (2010).
- Roco M.C. Nanotechnology Frontiers at 20 years of NNI / M.C. Roco. [Electronic resource]. URL: www.nseresearch.org/2020/ (accessed 17.09.2021)
- Alizadeh-Ghodsi M. State-of-the-Art and Trends in Synthesis, Properties, and Application of Quantum Dots-Based Nanomaterials / M.Alizadeh-Ghodsi, M. Pourhassan-Moghaddam, A. Zavari-Nematabad et al. // Part. Syst. Charact. – 2019. – № 36. – P. 1800302–1800322.
- Бричкин С.Б. Коллоидные квантовые точки: синтез, свойства и применение / Бричкин С.Б., Разумов В.Ф. // Успехи химии. – 2016. –Т. 85. – № 12. – С. 1297-1312.
- Porotnikov D. Progress and Prospects of Solution-Processed Two-Dimensional Semiconductor Nanocrystals / Porotnikov D., Zamkov M. // J. Phys. Chem. C. – 2020. – V. 124. – № 40. – P. 21895–21932.
- Жуков Н.Д. Исследование квантовых точек в мультизеренном слое планарно-торцевой микроструктуры / Жуков Н.Д., Ягудин И.Т., Абаньшин Н.П. и др. // Письма в ЖТФ. – 2020. – Том 46. – Вып. 21. – С. 40 – 43.
- Уравнение Шрёдингера // – [Электронный ресурс] – URL: https://ru.wikipedia. org/wiki/Уравнение Шрёдингера (дата обращения 17.09.2021)
- Kittel C. Qwantum Theory of Solids / C. Kittel. John Wiley & Sons, INC. New-York – London. 1963.
- Драгунов В.П. Основы наноэлектроники / Драгунов В.П., Неизвестный И.Г., Гридчин В.А. – Логос, М., 2006. – 495 с.
- Волна де Бройля // Вики – [Электронный ресурс] – URL: https://ru.wikipedia. org/wiki/Волна де Бройля (дата обращения 17.09.2021)
- Метод МРРК // Гугл-наука – [Электронный ресурс] – URL: https://www.google. com/search?q=...=baMRRKp (дата обращения 17.09.2021)
- Жуков Н.Д. Синтез, фото- и катодолюминесцентные свойства коллоидных квантовых точек CdSe, CdTe, PbS, InSb, GaAs. / Жуков Н.Д., Крыльский Д.В., Шишкин М.И. и др. // Физика и техника полупроводников. – 2019. – Том 53. – Вып. 8. – С. 1103-1109. DOI: 10.21883/FTP.2019.08.48002.9037
- Сурис Р.А. Блоховские осцилляции в сверхрешетках из квантовых точек. / Сурис Р.А., Дмитриев И.А. // Успехи физических наук . – Том 173. – № 7. – С. 769 – 776.
- 23 Жуков Н.Д. Особенности свойств полупроводников АIIIВV в мультизеренной наноструктуре / Жуков Н.Д., Кабанов В.Ф., Михайлов А.И. и др. // Физика и техника полупроводников. – 2018. – Том 52. – Вып. 1. – С. 83 – 88.
- Крыльский Д.В. Синтез и свойства больших квантовых точек антимонида индия / Крыльский Д.В., Жуков Н.Д. // Письма в ЖТФ. – 2020. – Том 46. – Вып. 18. – С. 15 – 18.
- Мартинсон Л.К. Квантовая физика / Мартинсон Л.К., Смирнов Е.В. – [Электронный ресурс] – URL: http://fn.bmstu.ru/data-physics/library/physbook/tom5/ch4/texthtml/ch4_5.htm (дата обращения 17.09.2021)
- Клетка // Вики – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki/Клетка (дата обращения 17.09.2021)
- Франк‑Каменецкий М.Д. Самая главная молекула. От структуры ДНК к биомедицине XXI века / Франк‑Каменецкий М.Д. – М: Альпина нон‑фикшн, 2017. ISBN 978‑5‑9614‑4522‑0.
- ДНК // Яблик – [Электронный ресурс] – URL: https://yablyk.com/005155-what-is-dna-in-simple-words/ (дата обращения 17.09.2021)
Список литературы на английском языке / References in English
- Materija [Matter] // Wiki - [Electronic resource] - URL: https://ru.wikipedia.org/wiki / Matter(physics) (accessed 17.09.2021) [in Russian]
- Istorija mikroskopa [The history of the microscope] // 4 eyes - [Electronic resource] - URL: https://4glaza-irkutsk.ru / statistics/brief-history-of the microscope (accessed 17.09.2021) [in Russian]
- Mir obojdjonnyh velichin [The world of bypassed quantities] // Andronum - [Electronic resource] - URL: https: //andronum.com/product/ostvald-v-mir-oboydennyh-velichin / (accessed 17.09.2021) [in Russian]
- Nanotehnologija [Nanotechnology] // Wiki - [Electronic resource] - URL: https://ru.wikipedia.org/wiki/Nanotechnology (accessed 17.09.2021) [in Russian]
- TanigutiNorio // Wiki - [Electronic resource] – URL: https://ru.wikipedia . org/wiki/ <url> (09/17/2021) [in Russian]
- Nanomaterial [Nanomaterial] // Wiki - [Electronic resource] – URL: https://ru.wikipedia.org/wiki/Nanomaterial (accessed 17.09.2021) [in Russian]
- Nanotehnologija [Nanotechnology] // Neftegaz – [Electronic resource] - URL: https://neftegaz.ru/tech-library/tekhnologii/141844-nanotekhnologii/Nanotechnology (accessed 17.09.2021) [in Russian]
- Nanonauka [Nanoscience] // Wiki - [Electronic resource] - URL: https://ru.wiktionary.org/wiki/Nanoscience (accessed 17.09.2021) [in Russian]
- Glukhova O.E. Osnovy nanoindustrii [Fundamentals of Nanoindustry] / Glukhova O.E., Gorokhovsky A.V., Zhukov N.D. et al. - Saratov: Publishing house of Sara unita, 2009. - 384 p. ISBN 978-5-292-03982-2. [in Russian]
- Lok S. Nanotechnology: Small miracles / C. Lok // Nature 467, 18 (2010).
- Roco M.C. Nanotechnology Frontiers at 20 years of NNI / M.C. Roco. [Electronic resource]. URL: www.nseresearch.org/2020/ (accessed 17.09.2021)
- Alizadeh-Ghodsi M. State-of-the-Art and Trends in Synthesis, Properties, and Application of Quantum Dots-Based Nanomaterials / M.Alizadeh-Ghodsi, M. Pourhassan-Moghaddam, A. Zavari-Nematabad et al. // Part. Syst. Charact. – 2019. – № 36. – P. 1800302–1800322.
- Brichkin S.B. Kolloidnye kvantovye tochki: sintez, svojstva i primenenie [Colloidal quantum dots: synthesis, properties and application] / Brichkin S.B., Razumov V.F. // Uspehi himii [Successes of Chemistry]. - 2016. -VOL. 85. - No. 12. - pp. 1297-1312. [in Russian]
- Porotnikov D. Progress and Prospects of Solution-Processed Two-Dimensional Semiconductor Nanocrystals / Porotnikov D., Zamkov M. // J. Phys. Chem. C. – 2020. – V. 124. – № 40. – P. 21895–21932.
- Zhukov N. D. Issledovanie kvantovyh tochek v mul'tizerennom sloe planarno-torcevoj mikrostruktury [Study of quantum dots in a planar layer multiarena the end of microstructure] / Zhukov N. D., Yagudin I. T., Amonsin N. P. et al. – 2020. – Vol. 46. – Vol. 21. – P. 40 – 43. [in Russian]
- Uravnenie Shrjodingera [The Schrodinger equation] - [Electronic resource] - URL: https://ru.wikipedia . org/wiki/Schrodinger equation (accessed 17.09.2021) [in Russian]
- Kittel C. Qwantum Theory of Solids / C. Kittel. John Wiley & Sons, INC. New-York – London. 1963.
- Dragunov V.P. Osnovy nanojelektroniki [Fundamentals of nanoelectronics] / Dragunov V.P., Unknown I.G., Gridchin V.A. - Logos, M., 2006. - 495 p. [in Russian]
- Volna de Brojlja [De Broglie Wave] // Wiki - [Electronic resource] - URL: https://ru.wikipedia . org/wiki/De Broglie Wave (accessed 17.09.2021) [in Russian]
- Metod MRRK [MRRK method] // Google-science - [Electronic resource] - URL: https://www.google.com/search?q=...=bamrrkp (accessed 17.09.2021) [in Russian]
- Zhukov N.D. Sintez, foto- i katodoljuminescentnye svojstva kolloidnyh kvantovyh tochek CdSe, CdTe, PbS, InSb, GaAs [Synthesis, photo- and cathodoluminescent properties of colloidal quantum dots of cadmium selenide, cadmium telluride, PBX-based, gallium arsenide-based]. / Zhukov N.D., Dorsky.V., M Shishkin.I. et al. // Physics and technology of semiconductors. - 2019. - Volume 53. - Issue 8. - pp. 1103-1109. DOI: 10.21883/FTP.2019.08.48002.9037 [in Russian]
- Souris R.A. Blohovskie oscilljacii v sverhreshetkah iz kvantovyh tochek [Blokhov oscillations in quantum dot superlattices] / Suris R.A., Dmitriev I.A. // Uspehi fizicheskih nauk [Successes of physical sciences]. - Volume 173. - No. 7. - pp. 769-776. [in Russian]
- 23 Zhukov N.D. Osobennosti svojstv poluprovodnikov AIIIVV v mul'tizerennoj nanostrukture [Features of the properties of aiiibv semiconductors of compounds, compounds in a multigrain nanostructure] / Zhukov N.D., V. Kabanov.F., Mikhailov A.I. et al. // Fizika i tehnika poluprovodnikov [Physics and Technology of semiconductors]. - 2018. - Volume 52. - Issue 1. - pp. 83 - 88. [in Russian]
- Krylsky D.V. Sintez i svojstva bol'shih kvantovyh tochek antimonida indija [Synthesis and properties of large quantum dots of indium antimonide] / Krylsky D.V., Zhukov N.D. // Pis'ma v ZhTF [Letters in ZhTF]. - 2020. - Volume 46. - Issue 18. - pp. 15-18. [in Russian]
- L Martinson.K. Kvantovaja fizika [Quantum physics] / L Martinson.K., Smirnov E.V. - [Electronic resource] – URL-address: http://fn.bmstu.ru/data-physics/library/physbook/tom5/ch4/texthtml/ch4_5.htm (accessed 17.09.2021) [in Russian]
- Kletka [Cell] // Wiki - [Electronic resource] - URL: https://ru.wikipedia.org/wiki/Cell (accessed 17.09.2021) [in Russian]
- Frank Kamenetsky M.D. Samaja glavnaja molekula. Ot struktury DNK k biomedicine XXI veka [The most important molecule. From the structure of DNA to the biomedicine of the XXI century of the century] / Frank Kamenetsky M.D. - M: Alpina non-fiction, 2017. ISBN 978 5 9614 4522 0. [in Russian]
- DNK [DNA] // Yablik - [Electronic resource] - URL: https://yablyk.com/005155-what-is-dna-in-simple-words / (accessed 17.09.2021) [in Russian]