ВОЗМОЖНОСТИ ДИСТАНЦИОННОГО ОБУЧЕНИЯ В ПРЕПОДАВАНИИ ГЕОМЕТРИИ УЧАЩИМСЯ С ОСОБЫМИ ОБРАЗОВАТЕЛЬНЫМИ ПОТРЕБНОСТЯМИ
Быков А.А.1, Сенчилов В.В.2, Тимофеева Н.М.3, Киселева О.М.4, Тимофеева Т.И.5
1кандидат педагогических наук, доцент, 2кандидат физико-математических наук, 3кандидат педагогических наук, доцент, 4кандидат педагогических наук, доцент, 5магистрант,
1ФГБОУ ВО «Национальный исследовательский университет МЭИ» филиал в г. Смоленске,
2,3,4,5ФГБОУ ВО «Смоленский государственный университет»
Работа выполнена при поддержке гранта РФФИ № 17-16-67015
ВОЗМОЖНОСТИ ДИСТАНЦИОННОГО ОБУЧЕНИЯ В ПРЕПОДАВАНИИ ГЕОМЕТРИИ УЧАЩИМСЯ С ОСОБЫМИ ОБРАЗОВАТЕЛЬНЫМИ ПОТРЕБНОСТЯМИ
Аннотация
В статье описаны составляющие авторского дистанционного курса по геометрии для учащихся одиннадцатых классов с особыми образовательными потребностями. Представлены результаты педагогического эксперимента по его внедрению в ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска», демонстрирующие повышение эффективности преподавания школьного курса геометрии с опорой на разработанный курс. Изложены особенности разработки и применения заданий диалогового типа с использованием бесплатно распространяемых программ.
Ключевые слова: преподавание геометрии, дистанционное обучение, интерактивные технологии, обучение детей с ограниченными возможностями здоровья, развитие мышления.
Bykov A.A.1, Senchilov V.V.2, Timofeeva N.M.3, Kiseleva O.M.4, Timofeeva T.I.5
1PhD in Pedagogy, Associate professor, 2PhD in Physics and Mathematics, 3PhD in Pedagogy, 4Associate professor; PhD in Pedagogy, Associate professor, 5Master's Degree Student,
1FSBEI of HE National Research University MPEI, Smolensk branch
2,3,4,5FSBEI of HE Smolensk State University
POSSIBILITIES OF REMOTE TRAINING IN TEACHING GEOMETRY WITH STUDENTS WITH SPECIAL EDUCATIONAL NEEDS
Abstract
The article describes the components of the author's e-learning course on geometry for eleventh-grade students with special educational needs, presents the results of a pedagogical experiment on its implementation. The specifics of the development and application of interactive tasks using free distribution programs are described.
Keywords: teaching geometry, e-learning, interactive technologies, teaching children with disabilities, development of thinking.
В современной системе образования в последнее время широкое применение получило дистанционное обучение. Оно особенно важно для тех, кто в силу обстоятельств не может овладевать знаниями, используя классические традиционные формы и методы. Независимость от места и времени, возможность индивидуальных консультаций с преподавателем и максимального использования мультимедийных ресурсов – неоспоримые преимущества дистанционного образования. Однако его реализация требует разработки современных методических подходов, так как зачастую традиционные не дают желаемых результатов. Рассмотрим возможности применения дистанционного обучения в преподавании школьного курса геометрии.
К основным проблемам школьной геометрии, которая напрямую связана с формированием у учащихся наглядно-образного и абстрактно-логического мышления, помимо нехватки учебного времени можно отнести трудности у школьников при решении геометрических задач, так как они требуют в совокупности использования теоретических знаний, применения формул, доказательства утверждений, правильное построение чертежа. Дистанционное обучение обладает интерактивными и визуальными возможностями, обеспечивающими решение данных проблем. Использование дистанционного курса сокращает время на повторение материала за счет использования мультимедийных технологий, позволяет повысить наглядность и ускорить изучение теоретического материала на основе применения анимационных иллюстраций, обеспечивает формирование навыков самостоятельной работы на основе использования контролирующих тестов и проектных заданий.
Несмотря на преимущества дистанционного образования в преподавании школьной геометрии, существует ряд проблем. [1, С. 52] Во-первых, учащиеся обладают правом самостоятельно выбирать количество часов на изучение курса геометрии, во-вторых, уровень подготовки и уровень возможностей у разных обучающихся различный, в-третьих, необходимо обеспечить взаимодействие учителя и ученика, в-четвертых, обеспечить наглядность изучаемого материала. Только решение всех поставленных задач сделает уроки геометрии в дистанционном обучении продуктивными.
Решение первой и второй проблем обеспечивается разделением заданий на уровни сложности и учитель может выбрать необходимый ему материал в зависимости от выбранного объема обучения учащегося. Так, в начале каждой темы предлагается теоретический материал, представленный двумя уровнями сложности изучения. Первый уровень состоит из изложения основных понятий и теорем, а также разбора нескольких стандартных задач по данной теме. Второй предполагает изложение доказательства теорем и разбор задач не только стандартных, но и повышенного уровня сложности.
Проверка знаний учащихся также имеет многоуровневое построение. [2, C. 5] Так, тестов по проверке теоретического материала представлено два вида, первый проверяет только знание основных понятий и формул, а второй особенности усвоения доказательств основных теорем изучаемой темы. Тестирование по решению задач также разделено на два уровня. Каждая тема содержит домашнее задание и задачи из ЕГЭ по математике. [3] Такая концепция построения позволяет учителю обеспечить многоуровневое и всестороннее изучение курса геометрии, а также обеспечивает возможность освоения курса в зависимости от выбранного количества часов.
Наибольшие трудности с методической точки зрения представляют третья и четвертая проблемы. При дистанционном обучении нет возможности совместно с вызванным к доске учащимся производить по ходу решения задачи дополнительные построения, как это делается, например, в традиционном образовании. Существующие в сети Интернет дистанционные курсы по геометрии при решении задач содержат готовые чертежи и возможностью «дорисовать» не обладают. Поэтому, разрабатывая курс, на первом уровне необходимо обеспечить наглядность путем внедрения в учебный курс уже готовых тщательно продуманных геометрических чертежей. [4, C. 30] Второй уровень объяснения теоретического материала содержит стереометрические чертежи, при чем несколько. В начале представлен стандартный рисунок, на котором указаны первоначальные данные, потом по ходу доказательства теоремы представлены чертежи с нанесенными дополнительными построениями и в разных проекциях для лучшего представления и понимания проблемы. Такие заранее созданные рисунки позволяют экономить время на изучение материала, формируют пространственное воображение и оказывают серьезную помощь в работе учителя.
Задачи для самостоятельного решения на уроке также должны быть снабжены соответствующими чертежами, иллюстрирующими ход решения задачи. Разработанные геометрические иллюстрации позволят не только экономить время, но и оказывают помощь в решении задач, уменьшая количество ошибок, ликвидируя боязнь ошибиться, и обеспечивают помощь в развитии логического и пространственного мышления. Задачи для домашнего задания снабжать чертежами не надо, наоборот учащиеся самостоятельно должны сделать необходимые построения с помощью компьютерных программ или на обычном листе по их желанию, т.к. дистанционный курс обеспечивает возможность загрузки файлов с решением в систему для проверки их учителем.
При разработке готовых чертежей помощь могут оказать такие программы как наглядная математика, наглядная геометрия, сервисы Google Skitch, LearningApps и многие другие. [5] К тому же можно подобрать такие программные средства, которые позволяют делать трехмерные модели. Большинство приложений распространяются бесплатно, просты в управлении и не требуют от учителя дополнительных навыков работы и легко усваиваются при использовании.
Для решения проблемы организации взаимодействия учителя и ученика в каждом занятии курса представлены задания диалогового типа. [6, C. 69] Каждое такое задание представляет собой поэтапное решение задачи, причем лишь некоторые моменты решения уже указаны, а учащийся дописывает недостающие компоненты. Задания снабжены поэтапными чертежами, иллюстрирующими решение стереометрических задач. Сами чертежи можно выполнить с помощью любых графических программ, но после этого задача должна быть представлена на основе документа интерактивной доски. Интерактивная доска позволяет вносить записи в решение учащемуся и учителю одновременно, дорисовывать чертежи. [7, C. 111] Для решения стереометрических задач оптимальным является использование программ, позволяющих создавать трехмерные модели. Такую модель можно вращать, в результате это способствует формированию у учащегося пространственного воображения, а также позволяет лучше понять особенности задачи и тем самым быстрее подобрать необходимое решение. Кроме того, учитель обладает возможностью спрятать от ученика определенные компоненты решения, используя технологию слоев, которой обладают многие интерактивные доски, а потом сделать слой активным, чтобы учащийся проверил свое решение, сверив его с правильным. Диалоговые задания являются основой авторского дистанционного курса и позволили повысить его эффективность.
Эффективность разработанного дистанционного курса была проверена с помощью педагогического эксперимента. [8] В эксперименте были задействованы 36 учеников 11 класса дистанционного центра и 8 учителей математики. При проведении эксперимента учащиеся были поделены на две группы, одним курс геометрии одиннадцатого класса преподавался традиционными методами с использованием разработанных учителями презентаций и курсов, а обучение второй группы осуществлялось на основе описанного выше курса. В каждой группе были учащиеся, выбравшие разное количество часов в неделю и различный уровень подготовки, кроме того, все учителя в ходе эксперимента проводили занятия обычными методами и на основе разработанного курса, т.е. каждый учитель получил учеников из первой и второй группы. [9] Используемая система обеспечила чистоту эксперимента. Эксперимент осуществлялся в течение всего учебного года.
Для подтверждения эффективности разработанного курса знания учащихся проверялись контрольными, самостоятельными работами и срезами знаний, предложенными администрацией образовательного центра и департаментом образования области.
На основе результатов контрольных работ и срезов знаний были получены следующие данные, представленные в таблице 1.
Таблица 1 – Результаты формирующего этапа педагогического эксперимента по определению эффективности авторского дистанционного курса (%)
| Низкий уровень | Средний уровень | Уровень выше среднего | Высокий уровень | |
| Экспериментальная группа | ||||
| Теоретические знания | 0 | 2 | 9 | 7 |
| Практические умения | 0 | 3 | 9 | 6 |
| Мотивационный компонент | 0 | 1 | 7 | 10 |
| Контрольная группа | ||||
| Теоретические знания | 5 | 8 | 4 | 1 |
| Практические умения | 6 | 9 | 3 | 0 |
| Мотивационный компонент | 5 | 6 | 5 | 2 |

Рис. 1 – Сравнительный анализ уровня теоретических знаний в экспериментальной и контрольной группах
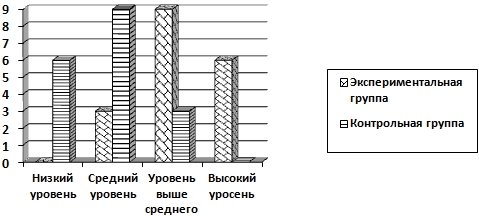
Рис. 2 – Сравнительный анализ уровня сформированности практических умений экспериментальной и контрольной групп
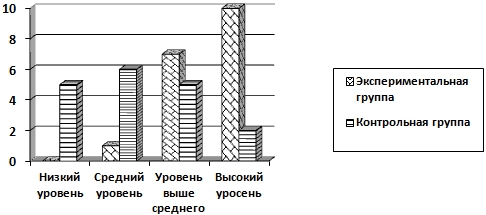
Рис. 3 – Сравнительный анализ уровня сформированности мотивационного компонента экспериментальной и контрольной групп
Представленные диаграммы показывают, что количественные показатели высокого и выше среднего уровней наличия знаний у учащихся контрольной группы ниже, чем в экспериментальной группе.
В экспериментальной группе по сравнению с контрольной на 33,2% больше количество обучающихся с высоким уровнем теоретической подготовленности, на 33,6% больше учеников с высоким уровнем практической подготовленности. Общий уровень мотивационного компонента также оказался выше в экспериментальной группе, чем в контрольной.
Для оценки достоверности результата эксперимента воспользуемся двусторонним критерием 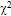 (хи-квадрат). [10, С. 122]
(хи-квадрат). [10, С. 122]
Обозначим Р1i вероятность достижения учащимися экспериментальной группы уровня сформированности знаний i, Р2i – вероятность достижения учащимися контрольной группы уровня i сформированности знаний.
Сформулируем нулевую гипотезу Н0: Р1i = Р2i, i = {1,2,3,4}. Нулевая гипотеза будет звучать так: в экспериментальных и контрольных группах учащиеся добились одинаковых результатов формирования знаний и умений. Альтернативная гипотеза Н1: Р1i ≠ Р2i – эксперимент дает положительный результат.
Рассчитаем наблюдаемое ![]() по формуле:
по формуле:
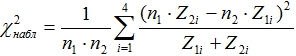
Число категорий мы берем равное 4, потому что у нас есть четыре уровня формирования знаний. Z1i – количество учащихся экспериментальной группы, достигших уровня i, Z2i – количество учащихся контрольной группы, достигших уровня i; n1 и n2 – количество элементов выборки экспериментальной и контрольной групп.
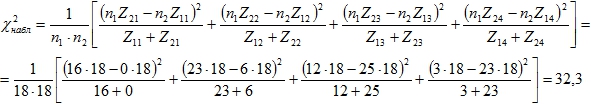
Число степеней свободы m = с – 1, с – число категорий (с = 4), а критическая область определяется неравенством ![]() , α в нашем случае 0,05. Наблюдаемое значение
, α в нашем случае 0,05. Наблюдаемое значение ![]() больше критического значения
больше критического значения ![]() , взятого из таблицы распределения, в результате гипотеза Н0 отвергается с вероятностью ошибки 0,05.
, взятого из таблицы распределения, в результате гипотеза Н0 отвергается с вероятностью ошибки 0,05.
Таким образом, мы получили достаточно оснований утверждать, что разработанный нами дистанционный курс положительно влияет на уровень знаний и умений учащихся.
Список литературы / References
- Ильина,Т.А. Структурно-системный подход к организации обучения / Т. А. Ильина. – М.: Знание, 1971. – Вып. 1. – 72 с.
- Козлов, С.В. Использование возможностей интеллектуальных информационных систем при организации дистанционного обучения / С. В.Козлов // NovaInfo.Ru – 2017. – Т. 2. – № 63. – С. 1–6.
- Сенчилов, В.В. Проблема организации совместной работы при дистанционном обучении математике детей с ограниченными возможностями здоровья / В.В. Сенчилов, А.А. Быков, О.М.Киселева, Н.М. Тимофеева // Постулат. – – № 9 (23). – С. 11. – URL: http://e-postulat.ru/index.php/Postulat/article/view/805/830 (дата обращения 15.11.2017).
- Сенчилов, В.В. Программное обеспечение дистанционного обучения математике детей с ограниченными возможностями здоровья / В.В.Сенчилов, А.А. Быков, Н.М. Тимофеева, О.М. Киселева // Научное обозрение: гуманитарные исследования. – 2017. – № 7. – С. 29-34.
- Киселева, М.П. Принципы интеграции информационных технологий в образовательный процесс / М.П. Киселева // Постулат. – 2017. – № 8 (22). – С. 6. – URL: http://e-postulat.ru/index.php/Postulat/article/view/777/800 (дата обращения 15.11.2017).
- Козлов, С.В. О подготовке школьников к участию в олимпиадах по информатике / С.В. Козлов // Психология, социология и педагогика. – 2015. – №1 (40). – С. 68-74.
- Сенчилов, В.В. Возможности программного обеспечения при дистанционном обучении математике детей с особыми образовательными потребностями / В.В. Сенчилов, А.А. Быков, О.М. Киселева, Н.М. Тимофеева // Евразийское научное объединение. – 2017. – Т. 2. – № 8 (30). – С. 111–112.
- Сенчилов, В.В. Модель подготовленности педагогов к преподаванию математики на основе дистанционного образования для детей с ограниченными возможностями здоровья / В.В. Сенчилов, А.А. Быков, О.М.Киселева, Н.М. Тимофеева // Постулат. – 2017. – №7. – С. 2. – URL: http://e-postulat.ru/index.php/Postulat/article/view/743/766 (дата обращения 15.11.2017).
- Сенчилов, В.В. Подходы к проектированию дистанционных курсов по обучению математике детей с ограниченными возможностями здоровья / В.В. Сенчилов, Н.М. Тимофеева, О.М. Киселева, А.А. Быков // Мир науки. – 2017. – Т. 5. –№ 4. – С. 7. – URL: https://mir-nauki.com/PDF/07PDMNpdf (дата обращения 15.11.2017).
- Алимухамбетова Г.Е. Теория педагогического процесса как основа формирования готовности школьников к познавательной деятельности / Г.Е. Алимухамбетова. – Алматы, 1994. – 134 с.
Список литературы на английском языке / References in English
- Il'ina, T.A. Strukturno-sistemniy podkhod k organizatsii obucheniya [Structurally-system Approach to Organization of Training] / T.A. Il'ina. - M.: Knowledge, 1971. - Is. 1. 72 p. [in Russian]
- Kozlov, S.V. Ispolzovaniye vozmozhnostey intellektualnykh informatsionnykh sistem pri organizatsii distantsionnogo obucheniya [Use of Capabilities of Intelligent Information Systems in Organization of Distance Learning] / S.V. Kozlov // NovaInfo.Ru - 2017. - Vol. 2. - No. 63. - P. 1-6. [in Russian]
- Senchilov, V.V. Problema organizatsii sovmestnoy raboty pri distantsionnom obuchenii matematike detey s ogranichennymi vozmozhnostiami zdorovya [Problem of Organization of Joint Work in E-learning of Mathematics of Children with Disabilities] / V.V. Senchilov, A.A. Bykov, O.M. Kiseleva, N.M. Timofeeva // Postulate. - 2017. - No. 9 (23). - P. 11. - URL: http://e-postulat.ru/index.php/Postulat/article/view/805/830 (Reference date: 15.11.2017). [in Russian]
- Senchilov, V.V. Programmnoye obespecheniye distantsionnogo obucheniya matematike detey s ogranichennymi vozmozhnostiami zdoroviya [Software for E-learning of Mathematics of Children with Disabilities] / V.V. Senchilov, A.A. Bykov, N.M. Timofeeva, O.M. Kiseleva // Scientific review: humanitarian research. - 2017. - No. 7. - P. 29-34. [in Russian]
- Kiseleva, M.P. Printsipy integratsii informatsionnykh tekhnologiy v obrazovatelniy protsess [Integration Principles of Informational Technologies in Educational Process] / M.P. Kiseleva // Postulate. - 2017. - No. 8 (22). - P. 6. - URL: http://e-postulat.ru/index.php/Postulat/article/view/777/800 (Reference date 15.11.2017). [in Russian]
- Kozlov, S.V. O podgotovke shkolnikov k uchastiyu v olimpiadakh po informatike [On Preparing of Students for Participation in Academic Competition on Computer Science] / S.V. Kozlov // Psychology, sociology and pedagogy. - 2015. - No. 1 (40). - P. 68-74. [in Russian]
- Senchilov, V.V. Vozmozhnosti programmnogo obespecheniya pri distantsionnon obuchenii matematike detey s osobymi obrazovatelnimi potrebnostiyami [Possibilities of Software for E-learning on Mathematics for Children with Special Educational Needs] / V.V. Senchilov, A.A. Bykov, O.M. Kiseleva, N.M. Timofeeva // Eurasian scientific association. - 2017. - T. 2. - No. 8 (30). - P. 111-112. [in Russian]
- Senchilov, V.V. Model podgotovlennosti pedagogov k prepodavaniye matematiki na osnove distantsionnogo obrazovaniya dlia detey s ogranichennimi vozmozhnostiami zdoroviya [Model of Teachers' Preparedness for Teaching Mathematics Based on E-learning of Children with Disabilities] / V.V. Senchilov, A.A. Bykov, O.M. Kiseleva, N.M. Timofeeva // Postulate. - 2017. - No. 7. - P. 2. - URL: http://e-postulat.ru/index.php/Postulat/article/view/743/766 (Reference date: 15.11.2017). [in Russian]
- Senchilov, V.V. Podkhody k proektirovaniyu distantsionnykh kursov po obucheniyu matematike detey s ogranichennymi vozmozhnostiami zdoroviya [Approaches to Development of E-learning Courses in Teaching of Mathematics for Children with Disabilities] / V.V. Senchilov, N.M. Timofeeva, O.M. Kiseleva, A.A. Bykov // The World of Science. - 2017. - T. 5. - No. 4. - P. 7. - URL: https://mir-nauki.com/PDF/07PDMN417.pdf (Reference date: 15.11.2017). [In Russian
- Alimukhambetova G.E. Teoriya pedagogicheskogo protsessa kak osnova formirovaniya gotovnosti shkolnikov k poznavatelnoy deyatelnosti [Theory of Pedagogical Process as Basis for Formation of Students' Readiness for Cognitive Activity] / G.E. Alimukhambetov. - Almaty, 1994. - 134 p. [in Russian]
