Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА ПО ДИСЦИПЛИНАМ МАТЕМАТИЧЕСКОГО ЦИКЛА

Научная статья
Булычева Ю.В.
Ильясова А.К.
DOI:
https://doi.org/10.23670/IRJ.2018.67.055
Выпуск: № 1 (67), 2018
Опубликована:
2017/12/29
PDF

Булычева Ю.В.1, Ильясова А.К.2

1Кандидат педагогических наук, 2кандидат физико-математических наук,

Астраханский государственный технический университет

УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА ПО ДИСЦИПЛИНАМ МАТЕМАТИЧЕСКОГО ЦИКЛА

Аннотация

При организации учебного процесса по дисциплинам математического цикла в технических университетах возникла острая необходимость внедрения в него системной самостоятельной работы студентов и создания её качественного учебно-методического сопровождения, включающего актуальные для направления подготовки и специальности формы и методы. В статье рассматриваются некоторые формы внеаудиторной самостоятельной работы студентов, обосновывается их эффективность для развития потенциальных возможностей мышления будущих специалистов. Приводятся учебно-методические разработки авторов для выполнения самостоятельной работы при изучении теоретического материала по алгебре и геометрии и математическому анализу студентами информационных направлений. Ключевые слова: математические дисциплины, самостоятельная работа, формы обучения, опрос, собеседование.

Bulycheva Yu.V.1, Ilyasova A.K.2

1PhD in Pedagogy, 2PhD in Physics and Mathematics,

Astrakhan State Technical University

EDUCATIONAL AND METHODOLOICAL SUPPORT FOR STUDENTS' INDIVIDUAL WORK IN TECHNICAL UNIVERSITY ON DISCIPLINES OF MATHEMATICAL CYCLE

Abstract

When organizing the educational process on the disciplines of the mathematical cycle in technical universities, there is an urgent need to introduce a systematic students' individual work and the to develop its qualitative educational and methodological support, including forms and methods relevant for the speciality and specialization program. The article describes some forms of students' individual work, their effectiveness is proved for development of potential thinking possibilities of  future specialists. The educational and methodical development of the authors for performing individual work is presented in the study of theoretical material on algebra and geometry and mathematical analysis by students of information directions. Keywords: mathematical disciplines, individaul work, forms of education, interview. Поддержание и повышение качества профессионального образования остаются приоритетными задачами Высшей школы, продиктованными  современными тенденциями развития экономики страны. Российскому рынку нужны специалисты, готовые к саморазвитию, самообразованию, профессионалы, умеющие самостоятельно принимать правильные производственные решения, чаще всего в условиях неопределенности.  Реформа образования, проводимая в настоящее время, подразумевает переход от модели обучения к модели образования. Преподаватель выступает не только проводником знаний и координатором учебного процесса, но и мотиватором в системе этих знаний. В условиях быстро растущего научно-технического прогресса, доступности информации, когда приобретенные за время обучения знания могут потерять в любой момент свою актуальность, способность самостоятельно и быстро получать их, имеет огромное значение для будущего специалиста. Учебные планы и рабочие программы дисциплин, изучаемых в университете и предполагающих их самостоятельное освоение студентами, составляются на основе федеральных и локальных нормативных документов. В настоящий момент объём самостоятельной работы студентов (в академических часах), определяемый учебными планами по образовательным программам высшего образования, составляет более половины общей трудоемкости дисциплины. Тенденция к сокращению общего количества часов, и, в частности, аудиторных часов на изучение математических дисциплин в технических вузах имеет устойчивый характер (табл. 1).  

Таблица 1 – Динамика изменения трудоемкости дисциплин математического цикла с 2014 по 2017 г.г. на примере направления подготовки 09.03.01 «Информатика и вычислительная техника»  в Астраханском государственном техническом университете

Дисциплина Год начала подготовки Общая трудоемкость Внеаудиторная самостоятельная работа студентов (с учетом подготовки к экзамену)
Математический анализ 2014 9 зачетных единиц (324 часа) 144 часа
2015-2017 гг. 9 зачетных единиц (324 часа) 200 часов
Алгебра и геометрия 2014 5 зачетных единиц (180 часов) 90 часов
2015 – 2017 гг. 5 зачетных единиц (180 часов) 126 часов
Теория вероятностей и математическая статистика 2014 4 зачетных единицы (144 часа) 72 часа
2015-2017 г.г. 3 зачетных единицы (108 часов) 58 часов
Дискретная математика 2014 4 зачетных единицы (144 часа) 72 часа
2015-2017 г.г. 4 зачетных единицы (144 часа) 92 часа
  Эффективность относительно небольшого количества аудиторных занятий и правильная организация внеаудиторной самостоятельной работы студентов, учитывающая принцип вариативности обучения, потенциальные возможности обучающихся - основная задача для преподавателя университета сегодня. На практике внеаудиторная самостоятельная работа студентов является наиболее неорганизованной формой обучения [1], не имеет системного подхода и включает много традиционных методов изучения математического материала, таких, например, как подготовка к опросу и решение задач. В 2017 году в Астраханском государственном техническом университете преподавателями начата работа по разработке и размещению на образовательном портале методических указаний для студентов по выполнению самостоятельной работы. Методические указания являются приложением к рабочей программе каждой изучаемой дисциплины и отражают все виды внеаудиторной работы, запланированные в этой программе [2].  Описание каждого задания внеаудиторной самостоятельной работы включает: тему, требования к выполнению данного задания, порядок выполнения задания, требования к оформлению задания, рекомендуемые источники. Приводим некоторые наши разработки по дисциплинам «Математический анализ» и «Алгебра и геометрия» для студентов направления подготовки 09.03.01 «Информатика и вычислительная техника». Задание: подготовить ответы на контрольные вопросы к собеседованию по теме «Основные алгебраические структуры. Алгебраическая бинарная операция на множестве. Группа». Контрольные вопросы к собеседованию.
  1. Приведите пример множества и операции, которая не является алгебраической операцией на этом множестве.
  2. Является ли операция умножения вектора на число алгебраической операцией на множестве векторов плоскости? Ответ аргументируйте.
  3. Является ли пересечение множеств алгебраической операцией на множестве всех подмножеств некоторого множества А? Ответ аргументируйте.
  4. Объясните, почему сложение по модулю 4 не является алгебраической операцией на множестве {0,1,2,}
  5. Существует ли нейтральный элемент на множестве всех подмножеств множества А относительно операции пересечения? Ответ аргументируйте.
  6. Существует ли нейтральный элемент на множестве всех подмножеств множества А относительно операции объединения? Ответ аргументируйте.
  7. Для какого элемента во множестве всех подмножеств данного множества существует симметричный элемент относительно операции объединения?
  8. Приведите пример операции, которая не является алгебраической бинарной операцией на множестве всех подмножеств.
  9. Приведите пример операции, которая не является алгебраической операцией на множестве всех векторов плоскости.
  10. Можно ли говорить о существовании симметричного элемента для какого – либо элемента на множестве всех подмножеств множества А относительно операции пересечения? Ответ аргументируйте.
  11. Может ли существовать 2 нейтральных элемента на множестве А относительно операции «*»?
  12. Сколько всего существует нейтральных элементов на множестве А относительно операции «*»?
  13. Сколько существует симметричных элементов для элемента множества А относительно операции «*»?
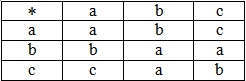
  14. Является ли операция «*», заданная на множестве {a,b,c} таблично (табл. 2), коммутативной.

Таблица 2 – Операция, определенная на множестве {a,b,c}

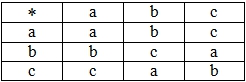
01-03-2018 18-37-05

  1. Является ли множество {0} группой относительно операции умножения?
  2. Образует ли группу множество нечетных чисел относительно операции сложения?
  3. Является ли множество {0} подгруппой группы {0,1,2} относительно операции сложения по модулю 3?
  4. Проверьте, является ли группой множество {a,b,c}относительно операции «*», заданной таблично (табл. 2).
  5. Приведите пример группы, которая не является абелевой.
  6. Найдите подгруппы первого и второго порядков для множества {a,b,c,d} относительно операции«*», заданной таблично (табл. 3).

Таблица 3 – Операция, определенная на множестве {a,b,c,d}

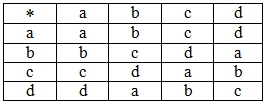
01-03-2018 18-39-53

  1. Алгебраическая операция задана таблично (табл. 4).
 

Таблица 4 – Операция, определенная на множестве {a,b,c}

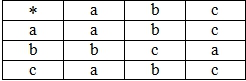
01-03-2018 18-40-39

Образует ли группу множество {a,b,c} относительно этой операции? Есть ли на этом множестве нейтральный элемент? Ответ аргументируйте.
  1. Алгебраическая операция задана таблично (табл. 5).

Таблица 5 – Операция, определенная на множестве {a,b,c}

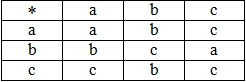
01-03-2018 18-41-36

Образует ли группу множество {a,b,c} относительно этой операции? Есть ли на этом множестве симметричный элемент для с?
  1. Алгебраическая операция задана таблично (табл. 6).

Таблица 6 – Операция, определенная на множестве {a,b,c}

01-03-2018 18-42-20

Образует ли группу множество {a,b,c} относительно этой операции? Требования к выполнению данного задания:
  1. Прочитайте конспект лекций, учебные пособия по темам, выносимым на собеседование.
  2. Осмыслите основное содержание математического текста, включая определения понятий и доказательства утверждений, разбор примеров.
  3. Читая изучаемый материал, подразделяйте его на основные смысловые части, выделяйте главные мысли, выводы. Постарайтесь привести собственные примеры и контрпримеры.
  4. Выделите в тексте существенные положения изучаемого материала, включая примеры и контрпримеры.
Порядок выполнения задания:
  1. Изучите рекомендованные источники информации по теме собеседования.
  2. Подготовьте ответы на контрольные вопросы по теме собеседования с подробным описанием.
Требования к оформлению задания: Оформление ответов на контрольные вопросы собеседования необходимо проводить в письменной форме. Рекомендуемые источники: (указываются информационные источники, прописанные в рабочей программе). В качестве альтернативы традиционной форме контроля усвоения теоретического материала – опроса определений понятий, утверждений теорем мы предлагаем собеседование со студентами по вопросам - заданиям, выданным заранее. Особенно это касается тем и разделов «совсем новых» для студентов, того математического материала, с которым они не сталкивались в школе. Например, тема «Основные алгебраические структуры» программы дисциплины «Алгебра и геометрия» очень сложна для восприятия студентов, поскольку требует от них непривычного взгляда на алгебру как науку о множествах с операциями, понимания возможности взглянуть с единой точки зрения на различные по своей природе, но одинаковые по структуре математические объекты. Предлагаемые нами вопросы к собеседованию не требуют формулировок понятий или утверждений, они требуют понимания этих понятий. Мы предлагаем вопросы, на которые студенты не найдут ответы в интернете. Они мотивируют думать, отвечать не односложно, математически грамотно аргументировать ответ и реализуют, на наш взгляд, принципы неопределенности, сложности и разнообразия в обучении. Многие из этих вопросов связаны с абстрактными множествами объектов, их свойствами, что помогает студенту выяснить глубину понимания изучаемого материала. Для некоторых вопросов, возможно, понадобятся вопросы – «подсказки», помогающие студенту в самостоятельных поисках правильного ответа или объяснения. Например, вопрос 23 из выше приведенного перечня можно сопроводить следующими вопросами: существует ли на множестве {a,b,c} нейтральный элемент; существует ли симметричный элемент для  b; сколько симметричных элементов для b можно указать; какая аксиома группы нарушается для множества {a,b,c}. Далее можно предложить следующие задания: 1) найдите элементы множества {a,b,c}, для которых не выполняется ассоциативность операции; 2) проверьте ассоциативность операции для трех различных элементов множества; для трех элементов, из которых  только два являются одинаковыми; для трех одинаковых элементов;  3) сделайте вывод, почему в любой группе существует только один симметричный элемент для каждого. Описанная выше форма работы с теоретическим материалом используется и при изучении математического анализа. Приведем фрагмент задания по теме «Дифференциальное исчисление функции одной переменной», содержащий  вопросы для собеседования.
  1. Применима ли теорема производной сложной функции к функции 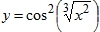01-03-2018 18-44-13в точке x=0?Ответ аргументируйте.
  2. Может ли существовать вторая производная 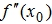01-03-2018 18-45-27, если не существует первая производная 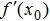01-03-2018 18-45-48? Ответ аргументируйте.
  3. Верно ли утверждение: если u(x) является дифференцируемой в точке x0, а v(x) не является дифференцируемой в точке x0, то функция u(x)+v(x) является дифференцируемой в точке x0? Ответ аргументируйте.
  4. Верно ли утверждение: если u(x) является дифференцируемой в точке x0, а v(x) не является дифференцируемой в точке x0, то функция  u(x)*v(x) не является дифференцируемой в точке x0 ? Ответ аргументируйте.
  5. Верно ли утверждение: если u(x) и v(x)не являются дифференцируемыми в точке x0, то функция u(x)+v(x)не является дифференцируемой в точке x0? Если утверждение неверно, привести соответствующий пример.
  6. Верно ли утверждение: если u(x) и v(x) не являются дифференцируемыми в точке x0, то функция  u(x)*v(x) не является дифференцируемой в точке x0? Если утверждение неверно, привести соответствующий пример.
Для того чтобы достичь желаемой результативности от самостоятельной работы студентов, преподавателю необходимо использовать дифференцированный подход к выбору форм и содержания заданий [3].  Они должны быть направлены не только на формирование объявленных в рабочих программах компетенций, но и учитывать индивидуальную траекторию развития студента [4]. Для этого нами начата работа по созданию банка задач и заданий различной сложности: репродуктивных и продуктивных вопросов по теоретическому материалу, открытых и закрытых тестовых заданий разного уровня, расчетно-графических и контрольных работ. Поскольку рабочие программы изучаемых в университете дисциплин  и методические указания к ним   составляются для каждого направления подготовки и специальности, эта работа требует колоссальных ресурсов времени и труда преподавателя. С другой стороны, благодаря ей, появляется реальная возможность избежать унификации в преподавании одних и тех же математических дисциплин для студентов разных направлений подготовки и специальностей.

Список литературы / References

  1. Леушин И.О. Некоторые проблемы организации самостоятельной работы студентов в техническом вузе/ И.О. Леушин, И.В. Леушина //Высшее образование в России. – 2017. - № 6 (213). - С. 51-56.
  2. Булычева Ю.В. Проектирование содержания рабочей программы дисциплины математического цикла в техническом вузе на основе результатов обучения/ Ю.В. Булычева, О.Н. Шамайло//Европейский журнал социальных наук. – 2016.- № 12. Том 2. - С. 173-180.
  3. Третьякова Е.М. Организация самостоятельной работы студентов как формы учебного процесса в вузе/ Е.М. Третьякова//Вектор науки ТГУ. Серия: Педагогика, психология. – 2015. - № 4(23). – С. 200 – 204.
  4. Булычева Ю.В. Классификация целей изучения дисциплин математического цикла в техническом университете на примере направления «Информационная безопасность» / Ю.В. Булычева, О.Н. Шамайло //Европейский журнал социальных наук. - 2015. - № 7. - С. 182 -188.
  5. Шахова Е.Ю. Анализ процесса формирования компетенций в ООП направления подготовки по ФГОС ВПО/ Е.Ю. Шахова, Л.В. Васильева//Достижения вузовской науки. – 2013. - № 7. – С. 157 – 163.
  6. Токтарова В. И. Математическая подготовка студентов: причины негативных тенденций/ В.И. Токтарова, С.Н. Федорова//Высшее образование в России. – 2017. - № 208(1). – С. 85 – 92.
  7. Булычева Ю.В. Организация самостоятельной работы студентов вузов при подготовке к тестированию по математике/Ю.В. Булычева, Т.В. Васильева//Вестник Астраханского государственного технического университета. – 2012. - № 2 (53). – С. 130 – 134.
  8. Сидняев Н.И. Концептуальные основы математического образования в техническом вузе / Н.И. Сидняев, С.К. Соболев // Высшее образование в России. - 2015. -  №7. – С. 36 – 41.
  9. Шамайло О.Н. Опыт использования деятельностного подхода в процессе обучения математике студентов технических вузов / О.Н. Шамайло, В.В. Серёгина // Европейский журнал социальных наук. - 2014. – Т.2. - № 10 – С. 455 – 461.
  10. Пак Ю.Н. Проблемы модернизации высшей школы в формате компетентностного подхода/Ю.Н. Пак, Ж.С. Нугужинов, Д.Ю. Пак // Высшее образование сегодня. - 2017. - № 10. – С. 48 – 52.

Список литературы на английском языке / References in English

  1. Leushin I.O. Nekotorye problemy organizacii samostojatel'noj raboty studentov v tehnicheskom vuze [Some problems of student individual work organization at the technical university] / I.O. Leushin, I.V. Leushina //Vysshee obrazovanie v Rossii [Higher Education in Russia]. – 2017. - No 6 (213). -  pp. 51-56. [in Russian]
  2. Bulycheva Y.V. Proektirovanie soderzhanija rabochej programmy discipliny matematicheskogo cikla v tehnicheskom vuze na osnove rezul'tatov obuchenija [ Projecting of the programme’s content of discipline of mathematical cycle at the technical institution of higher education on the basis of the results of teaching]/ Y.V. Bulycheva, O. N. Shamaylo// Evropejskij zhurnal social'nyh nauk [European Social Science Journal].  – 2016.- № 12.  V. 2. - P. 173-180. [in Russian]
  3. Tretyakova E.M. Organizacija samostojatel'noj raboty studentov kak formy uchebnogo processa v vuze [Organization of individual work of students as a form of educational process in the university] / Е.М. Tretyakova // Vektor nauki TGU. Serija: Pedagogika, psihologija [Vector of Science of Togliatti State University. Series: Pedagogy, Psychology]. – 2015. - № 4(23). – P. 200 – 204. [in Russian]
  4. Bulycheva Y.V. Klassifikacija celej izuchenija disciplin matematicheskogo cikla v tehnicheskom universitete na primere napravlenija «Informacionnaja bezopasnost'» [Classification of the purposes of studying disciplines of mathematical cycle at the Technical University on the example of course "Information Security"] / Y.V. Bulycheva, O. N. Shamaylo // Evropejskij zhurnal social'nyh nauk [European Social Science Journal]. - 2015. - № 7. - P. 182 -188. [in Russian]
  5. Shahova E.Ju. Analiz processa formirovanija kompetencij v OOP napravlenija podgotovki po FGOS VPO [Analysis of the process of forming competencies in basic educational program of the direction of training for the federal state educational standards of higher professional education]/ E.Ju. Shahova, L.V. Vasilyeva//Dostizhenija vuzovskoj nauki [Achievement of high school science]. – 2013. - № 7. – P. 157 – 163. [in Russian]
  6. Toktarova V.I. Matematicheskaja podgotovka studentov: prichiny negativnyh tendencij [Students’ Background in Mathematics: The causes of Negative Trends]/ V.I. Toktarova, S.N. Fedorova// Vysshee obrazovanie v Rossii [Higher Education in Russia]. – 2017. – No 208(1) - pp. 85 – 92. [in Russian]
  7. Bulycheva Y.V. Organizacija samostojatel'noj raboty studentov vuzov pri podgotovke k testirovaniju po matematike [Organization of individual work of students of a higher educational institution in preparation for testing in mathematics] / Y.V. Bulycheva, T.V. Vasilyeva//Vestnik Astrahanskogo gosudarstvennogo tehnicheskogo universiteta [Vestnik of Astrakhan state technical university]. – 2012. - № 2 (53). – P. 130 – 134. [in Russian]
  8. Sidnyaev N.I. Konceptual'nye osnovy matematichesko-go obrazovanija v tehnicheskom vuze [Conceptual basis for the improvement of mathematics education at technical university] / N.I. Sidnyaev, S.K. Sobolev // Vysshee obrazovanie v Rossii  [Higher Education in Russia].  -  2015. -  №7. – P. 36 – 41. [in Russian]
  9. Shamaylo O. N. Opyt ispol'zovanija dejatel'nostnogo podhoda v processe obuchenija matematike studentov tehnicheskih vuzov [Experience of using the activity approach in the process of teaching mathematics to the students of technical universities] / O. N. Shamaylo, V.V. Seregina // Evropejskij zhurnal social'nyh nauk [European Social Science Journal]. -  2014. – V. 2. - № 10. – P. 455 – 461. [in Russian]
  10. Pak Ju.N. Problemy modernizacii vysshej shkoly v formate kompetentnostnogo podhoda [Higher school modernization related issues in the format of a competency-based approach] / Ju.N. Pak, Zh.S. Nuguzhinov, D. Ju. Pak// Vysshee obrazovanie segodnja [Higher education today]. –  2017. – № 10. – P. 48 – 52. [in Russian]