ТЕСТИРОВАНИЕ ПРОГРАММ С УЧЕТОМ ГРАНИЧНЫХ УСЛОВИЙ и НЕКОРРЕКТНОСТИ ВХОДНЫХ ДАННЫХ
Наймушина О.Э.
Кандидат педагогических наук, Технологический институт-филиал «Национальный исследовательский ядерный университет «МИФИ»
ТЕСТИРОВАНИЕ ПРОГРАММ С УЧЕТОМ ГРАНИЧНЫХ УСЛОВИЙ и НЕКОРРЕКТНОСТИ ВХОДНЫХ ДАННЫХ
Аннотация
В статье рассмотрен порядок освоения студентами базовых конструкций алгоритмов: репродуктивный уровень и последующая модификация. Особое внимание уделяется тестированию программ, при котором проверяются граничные условия и работоспособность программы при некорректных входных данных.
Ключевые слова: алгоритм, программа, тестирование.
Naymushina O.E.
Pedagogical Sciences candidate, Technology Institute-branch «National Research Nuclear University MEPhI»
PROGRAMS TESTING TAKING INTO ACCOUNT THE BOUNDARY CONDITIONS AND INCORRECTNESS OF THE INPUT DATA
Abstract
The article considers the development order of the algorithms basic design by students: reproductive level and subsequent modification. Special attention is given to programs testing, checking boundary conditions and the efficiency of the program in case of incorrect input data.
Keywords: algorithm, program, testing.
Для многих специальностей и направлений бакалавриата вузов в пределах дисциплины «Информатика» производится обучение составлению программ на каком-либо языке, как правило, высокого уровня (Паскаль. VBA, C++ и т.д.). При этом предполагается, что студенты знакомы с основными принципами создания алгоритмов, рассмотренных в школе. Однако чаще всего при составлении программ студенты испытывают трудности именно при написании алгоритма, а не при его реализации на языке. Поэтому обучению умения составления алгоритмов перед (или параллельно с) обучением написания программ должно быть уделено большое внимание.
Пять особенностей алгоритмов и их отличие от методов вычислений подробно рассмотрены Д. Кнутом [1]:
- конечность;
- определенность;
- ввод;
- вывод;
- эффективность.
Постепенное усложнение задач, начиная с репродуктивного этапа, способствует лучшему пониманию алгоритмов, что непосредственно влияет на правильность составления программ. Репродуктивный уровень (уровень воспроизведения, знания-копии) является первым (иногда вторым) уровнем обучения согласно классификациям И. Я. Лернера, В.П. Беспалько и многих других авторов. Следующий уровень – творческий (знания-умения, применение), и он основывается на предыдущем [2, 3, 4, 5, 6]. Поэтому задачи, решение которых строится на базовых конструкциях и модификации ранее рассмотренных решений, легче осваиваются студентами.
После реализации программы на каком-либо языке необходимо провести ее тестирование. Согласно определению в программировании, тест – это процедура, которая позволяет либо подтвердить, либо опровергнуть работоспособность программы [7]. Тесты должны быть простыми и в то же время функциональными. Подход к тестированию, при котором известна структура тестируемого объекта, называется структурным; еще одно название такого подхода – метод белого, или стеклянного, ящика. В общем случае Международные стандарты DO-178B [8] устанавливают покрытие операторов (каждый оператор должен выполняться хотя бы один раз), покрытие решений (каждая точка входа и выхода программы должна быть пройдена хотя бы один раз) и модифицированное покрытие условий/решений (выполнение каждого условия — термы — в составе решения) [9].
Тестирование программы не рекомендуется осуществлять на завершающем этапе. Как только готов отдельный модуль программы, он должен быть протестирован; это способствует выявлению проблем на ранних этапах процесса разработки программного продукта, и обозначению рамок системного тестирования [10]. Итеративный (инкрементальный) процесс разработки, который обеспечивает постепенное наращивание программы (во многих источниках этот процесс носит название «итеративное расширение»), используется не только для разработки программных продуктов, но и при обучении основам алгоритмизации и программирования.
Как показывает практика, большинство ошибок, выявленных при тестировании программы, связано с неправильно составленным (или неполным) алгоритмом решения задачи. При составлении первых программ студенты должны научиться правильно составлять тесты; особое внимание необходимо уделять проверке граничных условий задач, которая является одним из важнейших методов тестирования [11]. Значение этого метода увеличивается при создании приложений, однако и на первых шагах обучения программированию необходимо предусматривать составление соответствующих тестов. Программы должны быть так же проверены на работоспособность при вводе некорректных данных, которые могут привести к ее прерыванию.
Как правило, изучение алгоритмов начинается с самого простого – линейной структуры. Обычно в задачах этой темы проверяется умение выражать нужную величину из формулы, которое формируется в результате освоения таких школьных предметов, как математика и физика.
Пусть необходимо написать программу для решения следующей задачи:
(1) По заданной площади грани куба найти его объем.
Если это первая программа студента, он может испытывать трудности при составлении алгоритма (и, соответственно, программы). Однако в том случае, если предварительно он ознакомлен с алгоритмом (или программой ввиду ее легкости) нижеприведенного задания, то трудности при написании программы практически будут отсутствовать:
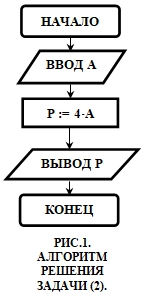
(2) Дана сторона квадрата а. Найти его периметр Р = 4 · а. [12, с. 10].
В данной задаче используется прямая формула (без преобразований), указанная в самом задании. Пример алгоритма решения задачи приведен на рис. 1, его реализация на VBA приведена ниже.
Sub p2()
Dim A As Integer, P As Integer
A = CInt(InputBox("Введите сторону квадрата а: "))
P = 4 * A
MsgBox ("Периметр равен " + CStr(P))End Sub
Тестирование программы сводится к вводу любого числа и проверке выходного значения как произведения введенного числа на 4. При вводе положительного числа ответ будет верен. Граничные условия следующие: 0 и большое положительное число. Некорректный ввод – отрицательное входное данное. Ввод отрицательных чисел и нуля не нарушает работоспособность программы, поэтому для пользователя необходимо предусмотреть вывод сообщения о таком значении, например: End Sub
…P = 4 * A If A < 0 Then MsgBox ("Введено отрицательное значение. Ответ некорректен.") End If MsgBox ("Периметр равен " + CStr(P))… При введении больших чисел (например, 9000 при базовых настройках) появляется предупреждение о переполнении и происходит прерывание программы. Поэтому необходимо ввести проверку и переход в конец программы: …A = CInt(InputBox("Введите сторону квадрата а: ")) If A > 900 Then MsgBox ("Введено большое число") GoTo Line1 End If… …Line1: End Sub Рассмотрев алгоритм решения этой задачи, решение задания (1) (рис.2) будет сводиться к модификации алгоритма (рис.1) и программы задания (2) (для упрощения программы объем вычисляется непосредственно через площадь): Sub p1() Dim S As Integer, V As Integer S = CInt(InputBox("Введите площадь S: ")) V = S ^ (3 / 2) MsgBox ("Объем равен " + CStr(V)) End Sub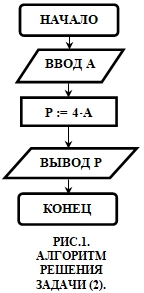
Легкость решения этой задачи при предварительном рассмотрении задачи (2) объясняется тем, что алгоритмы решения задач примерно одинаковы, и работа происходит на репродуктивном уровне.
При составлении алгоритмов и написании программ следует обратить внимание на присваивание переменным общепринятых имен. Он облегчает чтение программы другим человеком или самим автором, если прошло некоторое время после написания программы (в предыдущих листингах это стандартные обозначения периметра Р, стороны квадрата а, площади S и объема V). В дальнейшем это правило используется и развивается в коллективных разработках сложных программ и их комплексов.
Тестирование сводится к вводу корректных и некорректных значений и граничных условий. Если принять для задания (1) сторону куба, равной трем, то при вводе числа 9 (32) должен быть выведен результат 27 (33). Ввод значения 0 не изменяет ход работы программы. Аналогично рассмотренному выше примеру находится предельное наибольшее значение вводимого числа и путем проверки устанавливается переход в конец программы.
Ввод отрицательного значения площади также прерывает ход выполнения программы. Во избежание этого необходима проверка введенного значения S на положительность:
Sub p21()
Dim A As Integer, S As Integer, V As Integer
S = CInt(InputBox("Введите площадь S: "))
If S < 0 Then
MsgBox ("Введено отрицательное значение площади " + CStr(S))
GoTo Line1 End If If S > 1000 Then MsgBox ("Введено слишком большое число") GoTo Line1 End If V = S ^ (3 / 2) MsgBox ("Объем равен " + CStr(V)) Line1: End Sub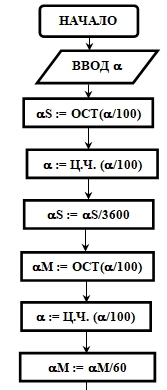
В начале освоения программирования при составлении тестовых наборов входных данных необходимо предусматривать все виды покрытий, о которых говорилось выше. Однако ввиду большого количества времени, затрачиваемого на такую процедуру, впоследствии, при приобретении опыта, при составлении алгоритмов решения не очень сложных программ особое внимание следует уделять покрытию решений.
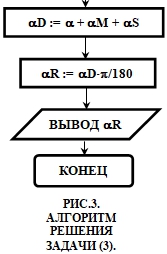
(3) Угол α задан в градусах, минутах и секундах. Найти его величину в радианах (с максимально возможной точностью). Тестирование: рекомендуется проверить работоспособность программы для углов, больших развернутого, а также для отрицательных углов [13, с. 19]. Автор заранее оговаривает условия тестирования, что имеет большое значение на начальных этапах освоения составления тестов. Если алгоритм будет предусматривать при считывании целого числа градусов только две позиции-цифры (до 99°), то очевидны ошибки при переводе в радианы углов, больших развернутого. Если в алгоритме предусмотрены операции деления величин углов или их частей в градусах, минутах или секундах, то это скажется на некорректной работе с отрицательными углами.
Один из вариантов алгоритма приведен на рис. 3, реализация решения на VBA будет иметь следующий вид:
Sub p3()
Dim pi
Dim AlphaD As Single, AlphaR As Single, AlphaS As Single, AlphaM As Single
Alpha = CSng(InputBox("Введите угол в формате (г)ггммсс: "))
AlphaS = Alpha Mod 100
Alpha = Alpha \ 100
AlphaS = AlphaS / 3600
AlphaM = Alpha Mod 100
Alpha = Alpha \ 100
AlphaM = AlphaM / 60
AlphaD = Alpha + AlphaM + AlphaS
pi = 4 * Atn(1)
AlphaR = AlphaD * pi / 180
MsgBox ("Угол в радианах равен " + CStr(AlphaR))
End Sub
Для тестирования, как предложено автором, можно взять такие углы, как 500°45¢45¢¢ и –500°45¢45¢¢. Но будут ли полученные результаты верными? Для контроля полученных значений желательно встроить в программу дополнительную проверку правильности преобразования величины угла (в градусах) в десятичную дробь:
…AlphaD = Alpha + AlphaM + AlphaS
MsgBox ("Угол в градусах равен " + CStr(AlphaD))
pi = 4 * Atn(1)…
Промежуточный вывод результатов покажет числа 500,7625 и -500,7625 соответственно. Согласно Д. Кнуту, алгоритм «считается эффективным, если все его операторы достаточно просты для того, чтобы их можно было точно выполнить в течение конечного промежутка времени с помощью карандаша и бумаги» [1, с.24]. Но если можно избежать «карандаша и бумаги» и использовать встроенный калькулятор, то проверять значения лучше (и точнее) с его помощью: набрав число 500,7625, нажать кнопку dms и получить исходные числа 500,4545 и –500,4545.
Таким образом, при обучении составления алгоритмов и их реализации в программах наилучшим путем является освоение базовых конструкций алгоритмов, и на их основе – постепенное усложнение задач; на первых этапах желательно предлагать модифицировать данные ранее алгоритмы (программы). Завершающим этапом составления любой программы является ее тестирование, которое должно предусматривать проверку граничных условий и работоспособность при некорректных входных данных.
Литература
- Кнут, Д.Э. Искусство программирования: в 3 т. – М. : Изд. дом Вильямс, 2012. – Т. 1: Основные алгоритмы. – 720 с.
- Лернер, И. Я. Дидактические основы методов обучения / И. Я. Лернер. – М. : Педагогика, 1981. – 186 с.
- Беспалько, В. П. Слагаемые педагогической технологии / В. П. Беспалько. – М. : Педагогика, 1989. – 192 с.
- Bloom, B. S. Taxonomy of Educational Objectives: The Classification of Educational Goals / B. S. Bloom. – Susan Fauer Company, Inc., 1956. – pp. 201-207.
- Симонов В.П. Диагностика личности и профессионального мастерства преподавателя. Учебное пособие для студентов педвузов, учителей и слушателей ФПК. – М.: Международная педагогическая академия, 1995. – 192 с.
- Симонов В.П. Проблема селективного подхода в образовании России и возможные пути его преодоления. [Электрон. ресурс]. Режим доступа: http://www.socpolitika.ru/rus/conferences/9300/9301/9303/document9366.shtml
- Бек, К. Экстремальное программирование: разработка через тестирование. Библиотека программиста / К. Бек. – С-Пб. : Питер, 2003. – 224 с.
- Библиографическое описание документа: Международный стандарт RTCA/DO-178B; введ. Dec. 1992 — RTCA Inc.
- Дастин, Э. Автоматизированное тестирование программного обеспечения. Внедрение, управление и эксплуатация /Э. Дастин, Д. Рэшка, Д. Пол. – М. : Издательство «Лори», 2003. – 568 с.
- Макгрегор, Д. Тестирование объектно-ориентированного программного обеспечения. Практическое пособие /Д. Макгрегор, Д. Сайкс. – К. : ООО «ТИД «ДС», 2002. – 432 с.
- Бейзер, Б. Тестирование черного ящика. Технологии функционального тестирования программного обеспечения и систем / Б. Бейзер. – С-Пб. : Питер, 2004. – 318 с.
- Абрамян, М. Э. 1000 задач по программированию. Ч.1. Скалярные типы данных, управляющие операторы, процедуры и функции / М. Э. Абрамян ; Ростовский гос. ун-т. – Ростов-на-Дону, 2004. – 43 с.
- Юркин, А. Г. Задачник по программированию / А.Г. Юркин. – СПб. : Питер, 2002. – 192 с.
