ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ШКОЛЬНОГО КУРСА МАТЕМАТИКИ НА ПОДГОТОВИТЕЛЬНЫХ КУРСАХ
ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ШКОЛЬНОГО КУРСА МАТЕМАТИКИ НА ПОДГОТОВИТЕЛЬНЫХ КУРСАХ
Научная статья
Бочкарев С.В.1, Кононенко Н.В. 2, *, Токарева Ю.С.3
2 ORCID: 0000-0002-0925-3624;
1 Читинский институт (филиал) Байкальского государственного университета, г. Чита, Россия;
2 Забайкальский государственный университет, г. Чита, Россия
* Корреспондирующий автор (kononenko.52[at]list.ru)
АннотацияВ работе предложена структурно-логическая модель обобщения и систематизации школьного курса математики. Модель представлена в виде трехмерной матрицы и имеет в своей основе блоки, полученные с помощью трех обобщающих признаков: вид объекта, вид задачи и уровень сложности. Более подробно в статье рассматривается описание уровней обобщающих признаков для курса алгебры и начал математического анализа. Данная модель апробирована на курсах по подготовке к ЕГЭ и позволяет увеличивать продуктивность обучения, создает предпосылки для выбора индивидуальной траектории обучения, расширяет возможности организации самостоятельной работы и способствует формированию основных универсальных учебных действий.
Ключевые слова: школьный курс математики, структурно-логическая модель, систематизация.
SUMMARISING AND SYSTEMISING SCHOOL MATHEMATICS COURSE DURING THE PRE-ENTRY COURSES
Research article
Bochkarev S. V.1, Kononenko N. V. 2, *, Tokareva Yu. S.3
2 ORCID: 0000-0002-0925-3624;
1 Chita Institute Baikal State University, Chita, Russia;
2 Transbaikal State University, Chita, Russia
* Correspondent author (kononenko.52[at]list.ru)
AbstractThis paper suggests a structural logical model for summarising and systematising the school Mathematics course. The model is submitted as a three-dimensional matrix based on the units acquired through three corporate features: object type, problem type, and complexity level. The article closely considers the description of the levels of the corporate features for the course of Algebra and Elements of Calculus. The model was tested during the preparation classes for the Unified State Exam [ЕГЭ]. It enables the increase in productivity of learning, creates the premises for choosing personal learning path, enhances the possibilities of organising the unsupervised study, and contributes to the development of the basic universal learning skills.
Keywords: school Mathematics course, structural logical model, systematising.
ВведениеАктуальность проблемы обобщения и систематизации содержания школьного курса математики обуславливается необходимостью сдавать обязательный единый государственный экзамен (ЕГЭ) по математике, слабой математической подготовкой многих выпускников, возможностью поступать в престижные вузы страны при наличии высоких баллов по ЕГЭ, тенденцией цифровизации процесса образования. Решение вопросов в данном направлении может быть использовано для целенаправленной работы по выявлению пробелов в знаниях учащихся, построения индивидуальных траекторий обучения в соответствии с имеющимися запросами и возможностями, разработки рабочих программ подготовительных курсов, создания компьютерных тренажеров, сайтов, порталов по подготовке к единому государственному экзамену и т. д.
Для подготовки к единому государственному экзамену значительная часть выпускников школ использует подготовительные курсы в очном, заочном или онлайн форматах. При такой форме подготовки необходимо учитывать следующие особенности.
Во-первых, подготовительные курсы не заменяют, а дополняют, продолжают, корректируют процесс обучения школьников. Поэтому, материал подготовительных курсов должен быть органично встроен в школьную программу и учитывать последовательность изучения тем в школьных программах [1], [2].
Во-вторых, основной целью подготовительных курсов является подготовка к сдаче ЕГЭ по математике, а, следовательно, они должны учитывать структуру контрольно-измерительных материалов, перечень проверяемых элементов, методические рекомендации по решению задач различного вида [3], [4], [6].
В-третьих, необходимо учитывать разнородный состав группы учащихся. Это, как правило, обучающиеся:
– с разным уровнем подготовки (слабые, средних способностей, сильные);
– с разной мотивацией (родители заставляют, достаточно пройти минимальный порог, получить как можно больше баллов для поступления в престижные вузы);
– с разными физиологическими особенностями и чертами характера (память, привычки, усердие, работоспособность, способы восприятия информации, дисциплинированность и др.);
– с разной систематичностью посещения занятий и отношением к выполнению домашних заданий (редкие или частые пропуски, выполняют или не выполняют домашние задания).
Следует отметить, что в открытых источниках информации слабо представлена систематизирующая составляющая, позволяющая установить и проследить различные структурно-логические связи между элементами школьного курса математики. Современные выпускники школ сталкиваются с определенными проблемами: при ориентации в большом массиве учебной информации; в понимании предлагаемых решений некоторых задач, использующих сведения из других разделов математики; в организации самостоятельной работы и т. п. На решение такого рода проблем направлены исследования по установлению понятных взаимосвязей между различными обобщенными блоками школьного курса математики, в том числе по созданию системы обобщенных блоков вместо их простого перечня.
Методы и принципы исследования
Целью данного исследования является разработка структурно-логической модели школьного курса математики.
При проведении исследовании использовались следующие теоретические методы: анализ литературы по теме исследования, методы анализа и синтеза, методы обобщения и классификации. В рамках исследования был проведен эксперимент с участием слушателей подготовительных курсов Читинского института Байкальского государственного университета.
Основные результатыРассмотрим, что необходимо учесть в разрабатываемой системе школьного курса математики, чтобы она была полезна при формировании универсальных учебных действий и применении различных методических систем обучения в условиях сетевого пространства. В. А. Тестов считает, что «процесс восприятия учеником нового материала в современных условиях становится все чаще нелинейным... Главной задачей школы становится нелинейное упорядочивание информации, приведение ее в систему» [7, С. 54].
Разрабатываемая в настоящее время система школьного курса математики призвана в какой-то мере помочь решить технологическую проблему новой парадигмы образования, заключающуюся в наполнении конкретным содержанием школьного курса математики в соответствии с общими неконкретизированными целями образования.
Это позволяет сформулировать следующие требования к разрабатываемой системе школьного курса математики [8], [10], [12]:
- нелинейность структуры курса математики;
- обучение через задачи;
- возможность формирования универсальных учебных действий через связь с другими дисциплинами, различные постановки математических задач и применение различных методов решения;
- наличие различных уровней сложности учебного материала;
- наличие системы взаимосвязей элементов содержания конкретного раздела математики, позволяющей как строить индивидуальную траекторию обучения, так и проводить диагностику возможных пробелов в знаниях;
- наличие стабильной системы обобщенных блоков учебного материала при динамичном изменении и совершенствовании их содержания в зависимости от поставленных целей;
- возможность самостоятельного обучения или в партнерстве с учителем.
Предлагаемая структурно-логическая модель обобщения и систематизации школьного курса математики в своей основе имеет обобщенные блоки, полученные с помощью трех обобщающих признаков: вид объекта, вид задачи и уровень сложности.
Более удачным вариантом модели представляется трехмерная матрица, которая позволяет максимально компактно накладывать уровни классификаций по рассматриваемым признакам друг на друга и обеспечивает, насколько это возможно, короткий путь между элементами. Для удобства ориентации в структуре матрицы проведем оси, содержащие соответствующие обобщающие признаки. Пусть ось Х отражает виды объектов, которые задают соответствующие строки матрицы; ось Y отражает виды задач, соответствующие столбцам матрицы; ось Z – уровни сложности, определяющие высоту расположения матрицы.
Итак, имеем следующий вид структуры модели, представленный на рисунке 1.
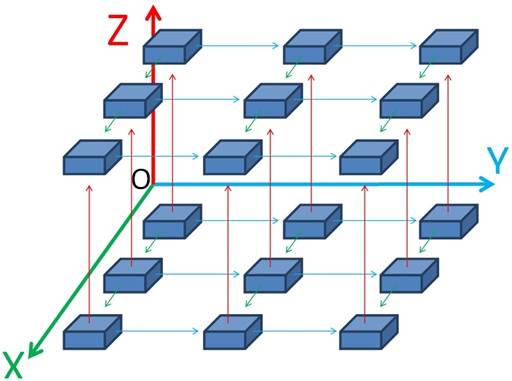
Рис. 1 – Структура модели обобщения и систематизации школьного курса математики
Достоинством модели данного вида является возможность применять линейную логику построения взаимосвязей между блоками в разрезе каждого обобщающего признака, что существенно упрощает процесс содержательного наполнения соответствующих блоков и позволяет не запутаться в назначении каждого перехода. В то же время модель позволяет строить нелинейную индивидуальную траекторию обучения, меняя направления переходов в зависимости от поставленных целей, или многократно повторять материал одного и того же блока, рассматривая его с точки зрения различных обобщающих признаков.
Предполагается построение трехмерной матрицы отдельно для алгебры и начал математического анализа, планиметрии и стереометрии. По сути, рассматриваемый раздел математики – это четвертый обобщающий признак, уровни которого не могут быть отражены в общей модели ввиду невозможности отображения четырехмерного пространства. Желательная последовательность переходов между уровнями этого признака следующая: алгебра и начала математического анализа планиметрия стереометрия.
Рассмотрим описание уровней обобщающих признаков для курса алгебры и начал математического анализа, так как в описании моделей обобщения и систематизации школьного курса планиметрии и стереометрии наблюдается гораздо меньше определенности.
Ось Х – виды объектов (выражений, уравнений, неравенств, функций):
- Линейные…
- Рациональные…
- Содержащие переменную под знаком модуля…
- Степенные с целыми показателями…
- Степенные с рациональными показателями...
- Показательные…
- Логарифмические…
- Тригонометрические...
Этот список остается неизменным при изучении объектов, прописанных в скобках.
Ось Y – виды задач:
- Вычислить…
- Преобразовать выражение…
- Решить уравнение…
- Решить неравенство…
- Решить систему уравнений (неравенств)...
- Решить задачу с параметрами алгебраическим методом…
- Решить задачу с параметрами функционально-графическим методом...
- Решить задачу с параметрами функциональным методом…
Предлагаемый перечень видов задач обусловлен необходимостью изучения соответствующих разделов.
Ось Z – уровни сложности:
- Простейшие задачи.
- Задачи, которые заменой переменной, разложением на множители, сопоставлением областей возможных значений сводятся к простейшим задачам.
- Задачи, которые с помощью предварительных преобразований, использующих свойства соответствующих функций, приводятся к задачам первых двух видов.
- Смешанные задачи, одновременно содержащие разные виды функций.
- Текстовые задачи, которые приводятся к решению задач предыдущих уровней.
Представленные уровни сложности в целом соответствуют выводам, полученным А. А. Прокофьевым [13], но с некоторыми поправками. Во-первых, задачи с параметрами и решение уравнений в целых числах были включены в состав всех уровней сложностей. В результате на последнем уровне сложности основной акцент делается на перевод текстовых задач на математический язык, т. е. по сути это уровень моделирования. Поскольку для некоторых функций достаточно сложно найти много текстовых задач, доступных пониманию школьнику, то предлагается включить в этот уровень также задачи предыдущих уровней сложности, но сформулированные словесно, без использования математических символов. Это тоже способ изучения математического языка через правильное использование математических терминов, понятий, понятное и однозначное описание порядка действий и т. п.
Во-вторых, средний уровень сложности предлагается разбить на три уровня ввиду большого объема материала, который может быть отражен на этом уровне. Это связано в основном с большим количеством формул, отражающих свойства соответствующих функций. Однако основных методов решения уравнений и неравенств, которые предлагается положить в основу при наполнении конкретным содержанием обобщенных блоков, немного.
Предлагается выделить три средних уровня сложности. Первый уровень нацелен на развитие навыков решения уравнений и неравенств с помощью замены переменной, разложения на множители или сопоставления областей значений. Второй – на тренировку применения формул для заданного вида функций. Третий – на развитие умений работать с формулами для разных видов функций в рамках одного уравнения или неравенства.
Таким образом, описание модели обобщения и систематизации школьного курса алгебры и начал математического анализа можно считать законченным. Во-первых, определена структура модели, имеющая три измерения. Во-вторых, для каждого измерения описаны его уровни. В-третьих, объяснена логика линейных взаимосвязей между обобщенными блоками этой трехмерной модели. Вдоль оси Х рассматривается применение одних и тех же методов, приемов, действий для разных видов объектов (выражений, уравнений, неравенств, функций). Вдоль оси Y рассматривается эволюция видов задач от простых вычислений до задач с параметрами для заданного вида объектов. Вдоль оси Z идет постепенное повышение уровня сложности для заданного вида задач и заданного вида объектов: простейшие варианты – использование различных формул и приемов для получения простейших вариантов – перевод текстовых задач на язык математических задач, которые с помощью формул и приемов приводятся к простейшим вариантам.
Приведем пример наполнения предметным содержанием обобщенных блоков этой модели в соответствии с предполагаемыми логическими взаимосвязями между ними.
В качестве ядра системы предлагается выбрать линию уравнений второго уровня сложности. Например, выберем метод замены переменной, приводящий к квадратному уравнению ![]() , тогда линия уравнений второго уровня сложности по видам объектов может иметь вид:
, тогда линия уравнений второго уровня сложности по видам объектов может иметь вид:
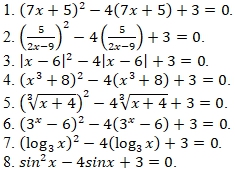
Далее преобразовываем эти уравнения с точки зрения различных уровней сложности. Первый уровень сложности – простейшие уравнения. Корни квадратного уравнения ![]() равны 1 и 3, поэтому рассматриваемые уравнения приводятся к соответствующим простейшим уравнениям. Третий уровень сложности – рассмотренные уравнения второго уровня дополняются необходимостью применения соответствующих формул. Четвертый уровень сложности – полученные уравнения второго уровня сложности дополняются функциями другого вида, причем полученные уравнения могут дублироваться для каждого вида функций. Пятый уровень сложности – уравнения третьего или четвертого уровня сложности формулируются словесно.
равны 1 и 3, поэтому рассматриваемые уравнения приводятся к соответствующим простейшим уравнениям. Третий уровень сложности – рассмотренные уравнения второго уровня дополняются необходимостью применения соответствующих формул. Четвертый уровень сложности – полученные уравнения второго уровня сложности дополняются функциями другого вида, причем полученные уравнения могут дублироваться для каждого вида функций. Пятый уровень сложности – уравнения третьего или четвертого уровня сложности формулируются словесно.
Таким образом, в модели оказываются заполненными (пока что по одному уравнению) 40 блоков, относящихся к уравнениям в разрезе всех видов этих уравнений и всех уровней сложности. Далее через каждый заполненный блок строится логическая цепочка задач вдоль оси Y, причем вначале отражаются вычисления и преобразования, используемые при решении уравнения, а после задачи усложняются путем перехода к соответствующим неравенствам и задачам с параметрами. В результате получатся 40 логических цепочек по 8 задач в каждой.
Предлагаемая теоретическая модель может быть заполнена конкретным предметным содержанием в соответствии с предполагаемыми взаимосвязями между обобщенными блоками. Очевидно, что это очень большая скрупулезная работа, результаты которой требуют хранения большого объема информации с возможностью доступа к ней в требуемой последовательности, в том числе в виде случайной выборки задач из каждого блока заданной последовательности. Все это обуславливает необходимость использования компьютерных программ и соответствующей базы данных, т.е. окончательная практическая реализация модели возможна только на стыке двух областей знания – математики и информатики. Данная модель может быть положена в основу структуры некоторого сайта, где посетители ресурса могли бы не только использовать готовую информацию, но и совершенствовать данную систему путем: предложения новых задач в рамках уже созданных логических цепочек; написания опорных конспектов для материала соответствующего обобщенного блока или всей цепочки; корректировки теоретического описания элементов структуры модели; оформления решений имеющихся в модели задач; предложения оптимальных способов маркировки задач с целью быстрого создания выборки, наиболее полно соответствующей запросам учащегося и т. п.
В рамках исследования в течение 2015-2019 гг. на базе подготовительных курсов при Читинском институте (филиале) ФГБОУ ВО «Байкальский государственный университет» проводились два этапа эксперимента: констатирующий и обучающий. В рамках проведенного эксперимента обучающимся предлагалось решить четыре группы задач.
I группа. Задачи на решение уравнений, расположенные в модели вдоль оси Z, между которыми существуют описанные взаимосвязи. Это: уравнения, которые с помощью замены переменной сводятся к квадратному уравнению и далее к простейшим; уравнения, которые с помощью преобразований сводятся к уравнениям предыдущих видов; уравнения, отличающиеся, от предыдущих, наличием двух видов функций. Всего было предложено шесть видов уравнений: рациональные, степенные, уравнения с корнями, показательные, логарифмические, тригонометрические. Для каждого вида приведены четыре взаимосвязанных уравнения, приводящихся к одному и тому же квадратному уравнению. От обучающихся требовалось решить как можно больше задач за ограниченное время.
II группа. Задачи с решениями, содержащими ошибку. От обучающихся требовалось определить, где сделана ошибка, и задачи какого вида надо решить, чтобы в дальнейшем не делать такой ошибки.
III группа. Задачи на решение шести простейших уравнений разных видов, расположенные в модели вдоль оси X. В этом случае требовалось решить каждое простейшее уравнение тремя разными способами.
IV группа. Задачи второго уровня сложности для шести видов функций: рациональные, степенные, функции с корнями, показательные, логарифмические, тригонометрические. Для каждого вида функций даны восемь взаимосвязанных задач, расположенных в модели вдоль оси Y. Это вычисления – преобразования – уравнения, неравенства и их системы – задачи с параметром. Обучающиеся должны были решить как можно больше задач за ограниченное время.
В помощь обучающимся предлагался справочный материал, содержащий сведения по решению простейших и квадратных уравнений и необходимые для решения свойства функций. Для решения задач каждой группы выделялось ограниченное время, недостаточное, чтобы успеть решить все задачи. Задачи были приведены в случайном порядке без соблюдения их логической последовательности в соответствующих цепочках и разбиения по видам. Задачи для констатирующего и обучающего экспериментов по методу решения и смыслу взаимосвязей были одинаковыми, но отличались коэффициентами соответствующих уравнений и применяемыми свойствами функций.
Условия проведения констатирующего и обучающего эксперимента отличались только тем, что при проведении обучающего эксперимента участникам была предварительно продемонстрирована на других примерах возможность построения цепочек взаимосвязанных задач и объяснена суть этих взаимосвязей. Всего в экспериментах участвовало 49 человек, обучающихся в мини-группах на курсах по подготовке к ЕГЭ. Полученные результаты по количеству решенных задач приведены в таблице 1.
Таблица 1 – Среднее количество решенных задач на одного участника
| Группа задач | Констатирующий эксперимент | Обучающий эксперимент |
| I | 9 | 15 |
| II | 11 | 19 |
| III | 7 | 9 |
| IV | 12 | 14 |
Результаты проведенных экспериментов показали существенный рост производительности при решении участниками задач первой группы. Здесь наблюдалось активное использование участниками возможности объединения задач в логически связанные «цепочки», что увеличивало скорость их решения. Причем некоторые участники решали сначала простые задачи, а потом переходили к более сложным задачам составленной «цепочки». А некоторые, наоборот, решали самую сложную задачу и на основе полученного решения сразу выписывали ответы для всех предыдущих уравнений соответствующей «цепочки». Полученный опыт работы составления последовательности задач позволил увеличить скорость решения задач и второй группы за счет возможности быстро указать требуемый вид уравнения в составленной «цепочке». При констатирующем эксперименте обучающиеся плохо понимали, как надо указать требуемый вид уравнения, и теряли много времени на его описание.
Небольшое увеличение решенных задач третьей и четвертой группы объясняется тем, что участники обучающего эксперимента уже встречались с соответствующей постановкой задач при проведении констатирующего эксперимента и поэтому психологически были лучше к ним готовы. Возможность построения логической последовательности задач здесь использовалась частично. При решении задач третьей группы участники, по-прежнему, старались использовать привычные для них методы, не понимая, зачем надо применять для решения этих задач другие, менее удобные для них методы. При решении задач четвертой группы большинство участников старались сначала решить наиболее простые задачи разных видов, а потом уже пробовали найти подходы к более сложным задачам, в том числе с помощью построения соответствующей «цепочки» задач. При этом попыток распространить последовательность на задачи с параметрами не наблюдалось.
Результаты исследования позволяют сделать следующие выводы.
- Эффективность самообучения и самодиагностики существенно возрастает, когда обучающиеся решают задачи с понятной для них логикой взаимосвязей между ними. Для сильных учеников можно предлагать решать сразу последние задачи последовательностей и, в случае их успешного решения, считать пройденным материал всех обобщенных блоков соответствующей последовательности. Это позволит определить уровень подготовки обучающегося и подобрать для него наиболее подходящую индивидуальную траекторию обучения.
- При разработке различных последовательностей задач надо учитывать необходимость предубеждения некоторых обучающихся в их неспособности решить задачи определенного вида. Поэтому требуется обязательное использование различных постановок задач, методов и способов их решения.
- При создании банка задач предлагаемой модели необходимо сразу предусмотреть многоуровневую систему учета, позволяющую осуществлять выборку заданий в разрезе требуемых последовательностей задач, постановок, методов и способов их решения, разделов, тем, формируемых универсальных учебных действий и т.д.
Обобщение и систематизацию содержания школьного курса математики предлагается проводить на основе трехмерной структурно-логической модели отдельно для алгебры и математического анализа, планиметрии и стереометрии. В работе определен состав качественных уровней каждого из трех измерений. Постоянный состав выделенных уровней обеспечивает стабильность структуры модели при возможности ее динамичного изменения и совершенствования содержания ее обобщенных блоков. Свойство динамичности модели предлагается использовать для создания различных логических последовательностей элементов модели, относящихся к разным блокам. Это позволит увеличить продуктивность обучения, создаст предпосылки для выбора индивидуальной траектории обучения для каждого обучающегося, расширит возможности организации самостоятельной работы, будет способствовать формированию основных универсальных учебных действий.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Беляева Е.А. Дидактические принципы построения комплексов учебных заданий, ориентированных на достижение личностных результатов школьников / Е.А. Беляева // Вестник Владимирского государственного университета имени Александра Григорьевича и Николая Григорьевича Столетовых. – 2019. – № 37 (56). – С. 123–133.
- Монатова А.А. Аналогия как принцип формирования содержания учебного материала в процессе математического образования / А.А. Монатова, М. В. Родионова // Вестник Владимирского государственного университета имени Александра Григорьевича и Николая Григорьевича Столетовых. – 2019. – № 38 (57). – С. 81–86.
- Лыкова К.Г. О проблемах внедрения элективного курса по математике в системе общего образования для развития вероятностного стиля мышления в условиях глобальной информатизации / К.Г. Лыкова // Continuum. Математика. Информатика. Образование. – 2019. – № 2 (14). – С. 82–90.
- Павлова Т.А. Подготовка к ЕГЭ по математике в малых группах / Т.А. Павлова, М. Н. Уварова // Ученые записки Орловского государственного университета. – 2019. – № 2 (83). – С. 296–300.
- Санина Е.И. Контекстные задачи по математике как средство развития функциональной грамотности обучающихся / Е.И. Санина, И. В. Насикан // Ученые записки Орловского государственного университета. – 2019. – № 1 (82). – С. 308–310.
- Соломахо Т.Б. Элективный курс «Различные методы решения уравнений и неравенств» для учащихся 11 класса / Т.Б. Соломахо //Державинский форум. – 2019. – Т. 3. – № – С. 111–116.
- Тестов В.А. Переход к новой образовательной парадигме в условиях сетевого пространства / В.А. Тестов // Инновации в образовании. Вестник Нижегородского университета им. Н.И. Лобачевского. – 2012. – № 4 (1). – С. 50–56.
- Гусев В.А.Теоретические основы обучения математике в средней школе: психология математического образования: учеб. пособие для вузов / В. А. Гусев. – М.: Дрофа, 2010. – 473 с.
- Кононенко Н.В. Реализация внутрипредметных связей в рамках содержательно-методических линий школьного курса математики / Н.В. Кононенко, Ю. С. Токарева, П. А. Чухрий // Самарский научный вестник. – 2019. – Т. 8. – № 3 (28). – С. 290–295.
- КурбановФ. Дидактические принципы в обучении математике / Ф.Курбанов // Гуманитарный трактат. – 2019. – № – С. 71–73.
- Поладова В.В. Краткий обзор педагогических технологий (в помощь молодому учителю математики) / В.В. Поладова // Sciences of Europe. – 2019. – № 43-2 (43). – С. 36–48.
- Попова Т.С. Обобщение знаний в процессе обучения математике как условие личностного развития учащихся / Т.С. Попова // Успехи современной науки. – 2017. – Т. 1. – № – С. 103–106.
- Прокофьев А. А. Рекомендации по выполнению заданий [Электронный ресурс] / А.А.Прокофьев. – URL: http://alexlarin.net/egehtml (дата обращения: 10.06.2019).
Список литературы на английском языке / References in English
- Belyaeva E. A. Didakticheskie principy postroeniya kompleksov uchebnyh zadanij, orientirovannyh na dostizhenie lichnostnyh rezul'tatov shkol'nikov [Didactic principles of construction of training tasks complexes focused on the achievement of personal learning outcomes] / E. A. Belyaeva // Vestnik Vladimirskogo gosudarstvennogo universiteta imeni Aleksandra Grigor'evicha i Nikolaya Grigor'evicha Stoletovyh [Bulletin of the Vladimir State University named after Alexander Grigorievich and Nikolai Grigorievich Stoletov]. – 2019. – № 37 (56). – P. 123–133. [in Russian]
- Monatova A. A. Analogiya kak princip formirovaniya soderzhaniya uchebnogo materiala v processe matematicheskogo obrazovaniya [Analogy as a principle of formation of content of educational material in the process of mathematical education] / A. A. Monatova, M. V. Rodionova // Vestnik Vladimirskogo gosudarstvennogo universiteta imeni Aleksandra Grigor'evicha i Nikolaya Grigor'evicha Stoletovyh [Bulletin of the Vladimir State University named after Alexander Grigorievich and Nikolai Grigorievich Stoletov]. – 2019. – № 38 (57). – P. 81–86. [in Russian]
- Lycova K. G. On the problems of introducing an elective course in mathematics in the general education system for the development of a probabilistic style of thinking in the context of global informatization [On the problems of implementation of elective course in mathematics in the system general education for the development of a probabilistic style of thinking in the terms of global informatization] / Lycova K. G. // Continuum. Matematika. Informatika. Obrazovanie [Continuum. Maths. Informatics. Education]. – 2019. – № 2 (14). – P. 82–90. [in Russian]
- Pavlova T. A. Podgotovka k EGE po matematike v malyh gruppah [Preparation for the math exam in small groups] / T. A. Pavlova , M. N. Uvarova // Uchenye zapiski Orlovskogo gosudarstvennogo universiteta [Scientific notes of Orel State University]. – 2019. – № 2 (83). – P. 296–300. [in Russian]
- Sanina E. I. Kontekstnye zadachi po matematike kak sredstvo razvitiya funkcional'noj gramotnosti obuchayushchihsya [Contextual tasks on mathematics as a means of development of functional literacy of students] / E. I. Sanina, I. V. Nasikan // Uchenye zapiski Orlovskogo gosudarstvennogo universiteta [Scientific notes of Orel State University]. – 2019. – № 1 (82). – P. 308–310. [in Russian]
- Solomakho T. B. Elektivnyj kurs "Razlichnye metody resheniya uravnenij i neravenstv" dlya uchashchihsya 11 klassa [Elective course "different methods of solving equations and inequations" for 11th grade students] / T. B. Solomakho // Derzhavinskij forum [Derzhavin Forum]. – 2019. – Т. 3. – № 10. – P. 111–116. [in Russian]
- Testov V. A. Perekhod k novoj obrazovatel'noj paradigme v usloviyah setevogo prostranstva [Transition to a new educational paradigm in the network space] / V. A. Testov // Innovacii v obrazovanii. Vestnik Nizhegorodskogo universiteta im. N.I. Lobachevskogo [Innovation in education. Bulletin of Nizhny Novgorod University named after N.I. Lobachevsky].– 2012. – № 4 (1). – P. 50–56. [in Russian]
- Gusev V. A. Teoreticheskie osnovy obucheniya matematike v srednej shkole: psihologiya matematicheskogo obrazovaniya: ucheb. posobie dlya vuzov [Theoretical foundations of teaching mathematics in secondary school: psychology of mathematical education: a textbook for universities] / V. A. Gusev. – М.: Drofa, 2010. – 473 p. [in Russian]
- Kononenko N. V. Realizaciya vnutripredmetnyh svyazej v ramkah soderzhatel'no-metodicheskih linij shkol'nogo kursa matematiki [Inter-subject links within the content-methodical lines of math school course] / N. V. Kononenko, J. S.Tokareva, P. A. Chukhriy // Samarskij nauchnyj vestnik [Samara Scientific Bulletin]. – 2019. – Т. 8. – № 3 (28). – P. 290–295. [in Russian]
- Kurbanov F. Didakticheskie principy v obuchenii matematike [Didactic principles in teaching mathematics] / F. Kurbanov // Gumanitarnyj traktat [Humanitarian treatise]. – 2019. – № 61. – P. 71–73. [in Russian]
- Poladova V. V. Kratkij obzor pedagogicheskih tekhnologij (v pomoshch' molodomu uchitelyu matematiki) [A brief overview of pedagogical technologies (to help a young mathematics teacher)] / V. V. Poladova // Sciences of Europe. – 2019. – № 43-2 (43). – P. 36–48. [in Russian]
- Popova T. S. Obobshchenie znanij v processe obucheniya matematike kak uslovie lichnostnogo razvitiya uchashchihsya [The synthesis of knowledge in the process of learning mathematics as a condition of personal development of students] / T. S. Popova // Uspekhi sovremennoj nauki [Advances in modern science]. – 2017. – Т. 1. – № 4. – P. 103–106. [in Russian]
- Prokof'ev A. A. Rekomendacii po vypolneniyu zadanij [Recommendations for completing tasks] [Electronic resource] / A. A. Prokof'ev. – URL: http://alexlarin.net/ege19.html (accessed: 10.06.2019). [in Russian]
