О ПРОВЕДЕНИИ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ТОПОЛОГИИ В ПЕДАГОГИЧЕСКОМ ВУЗЕ
О ПРОВЕДЕНИИ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ТОПОЛОГИИ В ПЕДАГОГИЧЕСКОМ ВУЗЕ
Научная статья
Ушаков А.В. *
ORCID: 0000-0002-7665-2086,
Московский городской педагогический Университет, Москва, Россия
* Корреспондирующий автор (oushakov1974[at]yandex.ru)
АннотацияДанная статья посвящена роли курса топологии для подготовки будущих учителей математики. Здесь рассматриваются различные аспекты педагогической направленности указанного курса. Особое внимание уделяется профессионализации обучения на практических занятиях по топологии. В статье приведены примеры задач, призванных оказать студентам педагогических вузов помощь в приобретении практических навыков, проиллюстрировать идеи и методы топологического исследования, обеспечить тем самым целостное усвоение всего материала.
Ключевые слова: высшая математика, топология, обучение, преподавание.
ON CONDUCTING PRACTICAL CLASSES IN TOPOLOGY IN PEDAGOGICAL UNIVERSITY
Research article
Ushakov A.V. *
ORCID: 0000-0002-7665-2086,
Moscow City University, Moscow, Russia
* Corresponding author (oushakov1974[at]yandex.ru)
AbstractThis article considers the role of a topology course in training future teachers of mathematics. Various aspects of a pedagogical orientation of the specified course are considered in the paper. Particular attention is paid to the professionalization of education in practical exercises on topology. The article presents examples of tasks intended to assist students of pedagogical universities in the acquisition of practical skills, to illustrate ideas and methods of topological research, thereby ensuring a holistic mastery of all the material.
Keywords: higher mathematics, topology, training, teaching.
Раздел «элементы топологии» играет весьма значительную роль для подготовки математиков вообще и учителей математики в частности. Вряд ли можно построить курсы математического анализа, дифференциальной геометрии, теории функций, отвечающие современному состоянию этих дисциплин, без привлечения топологических понятий. Кроме того, с ними постоянно приходится иметь дело в курсе элементарной геометрии: граничные и внутренние точки, геометрическое тело и его поверхность и т.п. Точное определение этим понятиям в школе, как правило, не дается, однако учитель должен иметь возможность обсудить их с учащимися старших классов на доступном уровне. Преподавать элементы топологии школьникам можно в рамках специального элективного курса, целесообразность проведения которого обусловлена следующими факторами: расширение кругозора учащихся; стимулирование интереса к математике в целом; повышение уровня строгости курса; развитие логического и абстрактного мышления; осуществление пропедевтики вузовского курса высшей математики. Необходимо также отметить большое прикладное значение топологических исследований, поэтому в процессе знакомства даже с простейшими топологическими структурами, учащиеся приходят к осознанию единой естественно-научной картины мира. Таким образом, топологию нужно изучать на различных уровнях математического образования:
- в школе на элективном курсе по наглядной топологии;
- в бакалавриате на различных спецкурсах;
- в магистратуре как базовый курс;
- в аспирантуре или на курсах повышения квалификации.
Нам представляется весьма актуальным, чтобы у школьников уже была сформирована база для топологического восприятия мира, а студенты – будущие учителя могли решать эту задачу. Основные направления для такой профессиональной ориентации вузовского курса топологии мы видим в явном выделении его методологической составляющей, в усилении внимания к различным приложениям топологии, а также в осуществлении пропедевтической линии, владение которой важно для учителя.
В итоге, цель курса топологии педагогического вуза состоит в освоении фундаментальных понятий и фактов соответствующего раздела геометрии, а также демонстрации их приложений к школьному курсу элементарной математики. Достижение этой цели предполагает решение следующих задач: сформировать систему базовых знаний по общей топологии; выработать навыки их практического применения в учебной или профессиональной деятельности; ознакомить с основными концепциями и направлениями развития современной геометрии; развить представления о топологической структуре окружающего мира.
Большим потенциалом для усиления для усиления профессионально-педагогической направленности обучения обладают практические занятия по топологии. Профессионализация обучения здесь может осуществляться через применение различных методов обучения; разбор примеров из школьных учебников по теме, связанной с текущим практическим занятием; моделирования ситуаций будущей профессиональной деятельности учителя.
На практические занятия по разделу «элементы топологии» традиционно выносятся следующие темы:
- Метрические пространства.
- Топологические пространства.
- Непрерывные отображения и гомеоморфизмы.
- Отделимость, компактность и связность.
- Топологические многообразия.
Остановимся на каждом из этих вопросов подробнее:
- Студенты должны знать определение и примеры метрических пространств (числовое пространство Rn с естественной метрикой). Уметь доказывать, что пространство является метрическим, т.е. проверять выполнение аксиом метрического пространства в каждом конкретном случае.
Знать определение открытых подмножеств метрического пространства, уметь доказывать их свойства.
Знать определение и признак непрерывного отображения метрических пространств.
- Знать определение и примеры топологических пространств (топология порожденная метрикой; дискретная и антидискретная топологии; примеры топологий на множестве из двух элементов).
Знать определения открытого и замкнутого множества; окрестности точки и множества; внутренней, внешней и граничной точек; внутренности, замыкания и границы множества. Уметь оперировать этими понятиями, строить соответствующие примеры, а также доказывать простейшие свойства типа:
дополнение замыкания множества совпадает с внутренностью дополнения этого множества;
замыкание множества есть объединение его внутренности с границей;
множество открыто тогда и только тогда, когда оно совпадает со своей внутренностью;
множество замкнуто тогда и только тогда, когда оно содержит свою границу и т.п.
Знать определение подпространства топологического пространства. Уметь строить топологию, индуцированную на подмножестве из пространства.
- Знать определение и признаки непрерывных отображений топологических пространств. Уметь проверять является ли данное отображение непрерывным или нет; доказывать непрерывность композиции непрерывных отображений и ограничения непрерывного отображения на подпространство.
Знать определение гомеоморфизма топологических пространств. Иметь представление о предмете топологии, как науки, изучающей свойства пространств, сохраняющиеся при гомеоморфизмах (или топологические инварианты).
- Знать определение таких топологических инвариантов, как отделимость, компактность и связность. Уметь проверять их наличие или отсутствие для конкретных пространств.
- Знать определение двумерного топологического многообразия и связанных с ним понятий: клеточного разложения, ориентируемости и эйлеровой характеристики.
Знать примеры многообразий (диск, сфера) и способ получения новых многообразий при помощи операции склеивания (лист Мебиуса, ручка, тор, бутылка Клейна, проективная плоскость). Уметь определять ориентируемо или нет каждое из построенных многообразий и подсчитывать их эйлерову характеристику. Иметь представление о классификации многообразий.
Практические занятия по топологии строятся, в основном, на решении задач, тщательный подбор которых играет важнейшую роль, особенно на уровне первоначального знакомства с этой дисциплиной. Дело в том, что строгие определения многих топологических понятий весьма громоздки, а содержательные теоремы появляются только после большой предварительной работы. Поэтому при разработке курса «элементы топологии» постоянно приходится решать вопросы, касающиеся отбора материала, зачастую ограничиваясь минимально необходимыми сведениями. В частности, на практических занятиях можно использовать лишь несколько сравнительно простых примеров топологических пространств и с их помощью проиллюстрировать все изученные теоретические факты. В результате одни и те же пространства становятся объектами серий задач, примеры которых приведены ниже.
Задача 1. Множество X состоит из трех элементов:
![]() . Под открытыми множествами будем понимать пустое множество, множество X и его подмножества
. Под открытыми множествами будем понимать пустое множество, множество X и его подмножества ![]()
- Доказать, что тем самым на множестве X задана топология τ.
- Найти все замкнутые множества топологического пространства (X, τ)
- Указать множества, которые являются одновременно открытыми и замкнутыми в X
- Найти границу, внутреннюю и внешнюю части множества
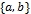
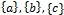 , а также замыкания множеств .
, а также замыкания множеств . - Является ли непрерывным отображение
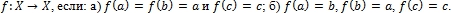
- Является ли пространство X отделимым или связным.
Решение. Оформим результаты выполнения операций объединения и пересечения элементов совокупности t в виде таблицы:
Таблица 1 – Операции над множествами в топологическом пространстве
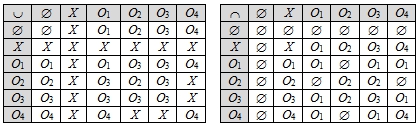
Таким образом, совокупность t замкнута относительно указанных операций, а значит, является топологией на множестве X.
Замкнутыми множествами являются пустое множество, само множество X, а также множества ![]() При этом множества O2 и O4 одновременно открыты и замкнуты.
При этом множества O2 и O4 одновременно открыты и замкнуты.
Множество открыто, а всякая окрестность точки c имеет с ним непустое пересечение, поэтому: ![]()
![]()
Замыкание множества есть наименьшее содержащее его замкнутое множество. В ходе решения задания 2) мы нашли все замкнутые множества пространства X. Теперь можно сразу записать, что: ![]()
Отображение а) является непрерывным, поскольку прообразы ![]() открытых множеств, открыты в X. Аналогично доказывается, что отображение б) не является непрерывным.
открытых множеств, открыты в X. Аналогично доказывается, что отображение б) не является непрерывным.
Пространство X можно представить в виде объединения ![]() двух непустых непересекающихся открытых множеств, поэтому оно является несвязным. Далее, любая окрестность точки c содержит точку a, поэтому у этих точек не существует непересекающихся окрестностей и пространство X не является отделимым.
двух непустых непересекающихся открытых множеств, поэтому оно является несвязным. Далее, любая окрестность точки c содержит точку a, поэтому у этих точек не существует непересекающихся окрестностей и пространство X не является отделимым.
Задача 2. Дана евклидова плоскость E2, на которой выбрана прямоугольная декартова система координат. Подмножество плоскости назовем открытым, если оно является пустым или вместе с каждой своей точкой содержит открытый круг ![]() , которому принадлежит точка.
, которому принадлежит точка.
- Доказать, что тем самым на плоскости задана топология (она называется концентрической)
- Доказать, что концентрическая топология обладает счетной базой.
- Выяснить, какие из множеств являются открытыми, какие замкнутыми, а какие ни открытыми, ни замкнутыми:
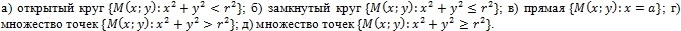
- Найти
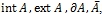 , если множество:
, если множество: 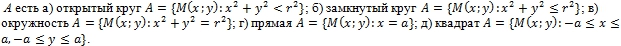
- Пусть на плоскости E2 даны три точки
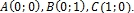 Найти все открытые множества пространства
Найти все открытые множества пространства 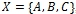 , топология которого индуцирована концентрической.
, топология которого индуцирована концентрической. - Выяснить, является ли непрерывным отображением: а) поворот вокруг начала координат; б) гомотетия с центром в начале координат; в) осевая симметрия, ось которой проходит через начало координат; г) параллельный перенос на ненулевой вектор.
- Пусть на плоскости E2 даны два луча
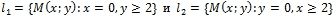 . Будет ли подпространство
. Будет ли подпространство 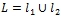 связным?
связным?
Решение. Из условия следует, что пустое множество и вся плоскость E2 являются открытыми множествами. Рассмотрим произвольную совокупность ![]() открытых множеств и точку
открытых множеств и точку ![]() . Тогда M0 принадлежит некоторому множеству
. Тогда M0 принадлежит некоторому множеству ![]() из рассматриваемой совокупности. По определению открытого множества, найдется открытый круг
из рассматриваемой совокупности. По определению открытого множества, найдется открытый круг ![]() со свойством:
со свойством: ![]() . Но
. Но ![]() , поэтому
, поэтому ![]() . Таким образом, множество O вместе со своей точкой M0 содержит открытый круг
. Таким образом, множество O вместе со своей точкой M0 содержит открытый круг ![]() , т.е. является открытым. Возьмем любые два открытых множества O1 и O2. Рассмотрим точку
, т.е. является открытым. Возьмем любые два открытых множества O1 и O2. Рассмотрим точку ![]() . Так как множества O1 и O2 открыты, то каждое из них вместе с точкой M0 содержит открытый круг
. Так как множества O1 и O2 открыты, то каждое из них вместе с точкой M0 содержит открытый круг ![]() соответственно. Пусть
соответственно. Пусть ![]() . Тогда
. Тогда ![]() . Таким образом, множество
. Таким образом, множество ![]() открыто.
открыто.
Ясно, что концентрическая топология обладает счетной базой, которая состоит из всех открытых кругов ![]() рационального радиуса r.
рационального радиуса r.
Задание 3) решим в случаях б) и г). Обозначим ![]()
![]() . Рассмотрим произвольно точку и содержащий ее открытый круг
. Рассмотрим произвольно точку и содержащий ее открытый круг ![]() с центром в начале координат. Тогда
с центром в начале координат. Тогда ![]() , следовательно,
, следовательно, ![]() . Для любого такого r0 множество
. Для любого такого r0 множество ![]() не содержится во множествах
не содержится во множествах ![]() . Таким образом, множество
. Таким образом, множество ![]() и его дополнение
и его дополнение ![]() не открыто и не замкнуто. Ответы для остальных пунктов задания 3): множество а) открыто; множество д) замкнуто, а множество в) не открыто и не замкнуто.
не открыто и не замкнуто. Ответы для остальных пунктов задания 3): множество а) открыто; множество д) замкнуто, а множество в) не открыто и не замкнуто.
Пусть ![]() . Ясно, что все точки открытого круга
. Ясно, что все точки открытого круга ![]() являются внешними точками множества A, так как в качестве их окрестности, содержащейся в
являются внешними точками множества A, так как в качестве их окрестности, содержащейся в ![]() , можно взять
, можно взять ![]() . Таким образом,
. Таким образом, ![]() . Рассмотрим произвольно точку
. Рассмотрим произвольно точку ![]() и ее окрестность O. Найдется открытый круг
и ее окрестность O. Найдется открытый круг ![]() со свойством
со свойством ![]() . В этом случае
. В этом случае ![]() , следовательно,
, следовательно, ![]() , а значит
, а значит ![]() . Окончательно имеем:
. Окончательно имеем: ![]() . Ответы для остальных пунктов задания
. Ответы для остальных пунктов задания
Точки B и C находятся на одинаковом расстоянии, равном единице, от начала координат A. Поэтому любое открытое множество, содержащее точку B, содержит также точки A и C. Далее, открытый круг с центром в начале координат и радиусом, меньшем единицы, содержит точку A, но не содержит точек B и C. Таким образом, открытыми множествами пространства X являются ![]()
![]() .
.
При гомотетии с центром в начале координат и коэффициентом k прообразом открытого круга радиуса r является открытый круг радиуса ![]() . Поэтому прообраз каждого открытого множества открыт и указанная гомотетия является непрерывным отображением. Ответы для остальных пунктов задания 6): отображения а), в) являются непрерывными; отображение г) не является непрерывным.
. Поэтому прообраз каждого открытого множества открыт и указанная гомотетия является непрерывным отображением. Ответы для остальных пунктов задания 6): отображения а), в) являются непрерывными; отображение г) не является непрерывным.
Ясно, что точки ![]() принадлежат всякому непустому открытому в L множеству, поскольку оно содержит пересечение множества L и открытого круга
принадлежат всякому непустому открытому в L множеству, поскольку оно содержит пересечение множества L и открытого круга ![]() с центром в начале координат радиуса
с центром в начале координат радиуса ![]() . Таким образом, любые два непустые открытые в L множества имеют непустое пересечение, поэтому пространство L связно.
. Таким образом, любые два непустые открытые в L множества имеют непустое пересечение, поэтому пространство L связно.
Задача 3. Пусть X есть бесконечное множество. Его подмножество назовем открытым, если оно либо пустое, либо совпадает с X, либо его дополнение до X является конечным множеством.
- Доказать, что тем самым на множестве X задана топология (она называется топологией Зарисского).
- Доказать, что в случае несчетного множества X, топология Зариского не имеет счетной базы.
- Для открытого в X множества A найти
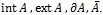 .
. - Доказать, что всякое непрерывное отображение пространства X на прямую E1 является постоянным.
- Доказать, что пространство X является компактным, но не отделимым.
Решение. Возьмем любые два открытых множества O1 и O2. Если одно из этих множеств пустое, то их пересечение этих пусто. Пусть теперь данные множества непустые. Тогда множество ![]() либо конечно, либо пусто, если
либо конечно, либо пусто, если ![]() . В любом случае заключаем, что множество
. В любом случае заключаем, что множество ![]() открыто в X. Рассмотрим произвольную совокупность
открыто в X. Рассмотрим произвольную совокупность ![]() открытых множеств. Без ограничения общности рассуждений, будем считать хоть одно из этих множеств непустым. Тогда множество
открытых множеств. Без ограничения общности рассуждений, будем считать хоть одно из этих множеств непустым. Тогда множество ![]() конечно или пусто, а значит множество
конечно или пусто, а значит множество ![]() открыто.
открыто.
Пусть множество X несчетно. Доказательство утверждения из задания 2) проведем методом от противного: предположим, что β есть счетная база в X. Выберем произвольно точку ![]() и определим множество
и определим множество ![]() . Если существует отличная от x точка
. Если существует отличная от x точка ![]() , то для открытого множества
, то для открытого множества ![]() найдется такое множество
найдется такое множество ![]() , что
, что ![]() . Это значит, что все множество M, а стало быть и точка y содержатся в V, что противоречит построению этого множества. Таким образом доказано, что
. Это значит, что все множество M, а стало быть и точка y содержатся в V, что противоречит построению этого множества. Таким образом доказано, что ![]() . Рассмотрим теперь дополнение
. Рассмотрим теперь дополнение ![]() и заметим, что в правой части этого равенства стоит счетное множество (как счетное объединение конечных множеств вида
и заметим, что в правой части этого равенства стоит счетное множество (как счетное объединение конечных множеств вида ![]() ), тогда как слева имеется несчетное множество
), тогда как слева имеется несчетное множество ![]() .
.
В ходе решения задания 1), мы видели, что любые два непустые открытые в X множества имеют непустое пересечение. Учитывая это замечание и свойства указанных в задании 3) операций, получаем: ![]() .
.
Предположим, что найдутся две различные точки ![]() и обозначим
и обозначим ![]() . Тогда ε – окрестности точек M и N не пересекаются, поэтому их прообразы при отображении f представляют собой непустые непересекающиеся открытые в X множества. С другой стороны, в пространстве с топологией Зариского любые два непустые открытые множества пересекаются. Таким образом, множество
. Тогда ε – окрестности точек M и N не пересекаются, поэтому их прообразы при отображении f представляют собой непустые непересекающиеся открытые в X множества. С другой стороны, в пространстве с топологией Зариского любые два непустые открытые множества пересекаются. Таким образом, множество ![]() состоит из одной точки, а само отображение f является постоянным.
состоит из одной точки, а само отображение f является постоянным.
Рассмотрим произвольное открытое покрытие Ω пространства X и множество ![]() . Тогда множество
. Тогда множество ![]() является конечным:
является конечным: ![]() . Обозначим через Oi такой элемент покрытия Ω, что
. Обозначим через Oi такой элемент покрытия Ω, что ![]() . Тогда
. Тогда ![]() есть конечное подпокрытие покрытия Ω.
есть конечное подпокрытие покрытия Ω.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Атанасян С. Л. Сборник задач по геометрии: учебное пособие для студентов III – IV курсов физико-математических факультетов педагогических вузов. В 2 ч. Ч. 2. / С. Л. Атанасян, Н. В. Шевелева, В. Г. Покровский. – М.: ЭКСМО, 2008. – 320 с.
- Атанасян С. Л. Геометрия 2: учебное пособие для вузов / С. Л. Атанасян, В. Г. Покровский, А. В. Ушаков. – М.: БИНОМ, 2015. – 544 с.
- Глизбург В. И. Гуманитарный потенциал обучения топологии и дифференциальной геометрии при подготовке учителя математики: Монография / В.И. Глизбург. – М.: МГСУ, М.: МГПУ, 2009. – 335 с.
- Ушаков А. В. Элементы топологии: методическое пособие для студентов 5 курса математического факультета / А.В. Ушаков. – М.: МГПУ, 2005. – 30 с.
- Ушаков А. В. Элементы топологии и дифференциальной геометрии: учебное пособие / А. В. Ушаков. – М.: МГПУ, 2010. – 144 с.
- Ушаков А. В. Из опыта проведения практических занятий по топологии со студентами педагогических вузов / А.В. Ушаков // Педагогические науки. – 2005. – № 5 (15). – С. 152-156.
- Ушаков А. В. О роли примеров на лекциях по топологии в педагогическом вузе / А. В. Ушаков // Педагогические науки. – 2012. – № 3 (54). – С. 74-84.
- Ушаков А. В. О роли примеров на лекциях по дифференциальной геометрии в педагогическом вузе / А. В. Ушаков // Педагогические науки. – 2014. – № 3 (66). – С. 31-34.
- Ушаков А. В. Использование информационных технологий при изучении геометрии в педагогическом вузе / А. В. Ушаков // Педагогические науки. – 2015. – № 2 (71). – С. 55-57.
- Педагогическая направленность математических дисциплин в подготовке будущих учителей математики: Монография / А. В. Ушаков, Ю. А. Семеняченко, В. Г. Покровский и др. – М.: Издательство «Спутник+», 2016. – 144 с.
Список литературы на английском языке / References in English
- Atanasyan S. L. Sbornik zadach po geometrii: uchebnoe posobie dlya studentov III – IV kursov fiziko-matematicheskih fakul'tetov pedagogicheskih vuzov. In 2 h the P. 2. [Compilation problems on geometry: a manual for students of III-IV courses of physics and mathematics faculties of pedagogy. In 2-x h.] / S. L. Atanasyan, N. V. SHeveleva, V. G. Pokrovskij. – M.: EHKSMO, 2008. – 320 p. [in Russian]
- Atanasyan S. Geometriya 2: uchebnoe posobie dlya vuzov [Geometry 2: textbook for high schools] / S.L. Atanasyan, V. G. Pokrovskij, A. V. Ushakov. – M.: BINOM, 2015. – 544 p. [in Russian]
- Glizburg V. I. Gumanitarnyj potencial obucheniya topologii i differencial'noj geometrii pri podgotovke uchitelya matematiki: Monografija [The humanitarian potential of learning topology and differential geometry in the preparation of teachers of Mathematics: Monograph] / I. Glizburg. – M.: MGSU, M.: MGPU, 2009. – 335 p. [in Russian]
- Ushakov A. V. Ehlementy topologii: metodicheskoe posobie dlya studentov 5 kursa matematicheskogo fakul'teta [Elements of the topology: a manual for students of the Faculty of mathematics course 5] / A. V. Ushakov. – M.: MGPU, 2005. – 30 p. [in Russian]
- Ushakov A. V. EHlementy topologii i differencial'noj geometrii: uchebnoe posobie [Elements of topology and differential geometry: a tutorial] / A. V. Ushakov. – M.: MGPU, 2010. – 144 p. [in Russian]
- Ushakov A. V. Iz opyta provedeniya prakticheskih zanyatij po topologii so studentami pedagogicheskih vuzov [From the experience of the practical lessons of the topology with the students of teachers colleges] / A. V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences]. – 2005. – № 5 (15). – P. 152-156. [in Russian]
- Ushakov A. V. O roli primerov na lekcijah po topologii v pedagogicheskom vuze [On the role of examples in lectures on topology in pedagogical university] / A. V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences]. – 2012. – № 3 (54). – P. 74-84. [in Russian]
- Ushakov A. V. O roli primerov na lekcijah po differencial'noj geometrii v pedagogicheskom vuze [On the role of examples in lectures on differential geometry in the pedagogical university] / A. V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences]. – 2014. – № 3 (66). – P. 31-34. [in Russian]
- Ushakov A. V. Ispol'zovanie informacionnyh tehnologij pri izuchenii geometrii v pedagogicheskom vuze [The use of information technology in studying geometry at the pedagogical university] / A. V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences]. – 2015. – № 2 (71). – P. 55-57. [in Russian]
- Pedagogicheskaja napravlennost' matematicheskih disciplin v podgotovke budushhih uchitelej matematiki: Monografija [Pedagogical orientation of the mathematical sciences in preparation of future teachers of mathematics: Monograph] / A. V. Ushakov, Ju. A. Semenjachenko, V. G. Pokrovskij and others – M.: Izdatel'stvo «Sputnik+», 2016. – 144 p. [in Russian]
