МЕТОД, ФОРМИРУЕМЫЙ В РАМКАХ ГРУППОВОЙ ФОРМЫ РАБОТЫ С СОЧЕТАНИЕМ ИНДИВИДУАЛЬНОГО ПОДХОДА
МЕТОД, ФОРМИРУЕМЫЙ В РАМКАХ ГРУППОВОЙ ФОРМЫ РАБОТЫ С СОЧЕТАНИЕМ ИНДИВИДУАЛЬНОГО ПОДХОДА
Научная статья
Акматкулов А.А.1, *, Абакирова Г.Ж.2, Мухтарбекова Р.М.3
1 ORCID: 0000-0002-5498-0281;
2 Кыргызский национальный университет им.Дж.Баласагына, Бишкек, Кыргызстан;
1, 3 Кыргызский государственный технический университет им. И.Раззакова, Бишкек, Кыргызстан
* Корреспондирующий автор (aakmatkulov[at]inbox.ru)
АннотацияВ статье отражены вопросы преподавания на примере обучения методам математического моделирования в экономике. Подтверждено, что при использовании групповой формы работы, эффективность обучения зависит от комплекса субъективных факторов, определяемых объемом работы и отношением студентов к практической деятельности. Выявлено, что групповая форма работы с сочетанием индивидуального подхода оказывает большое влияние на мотивацию учебной деятельности. Несомненным достоинством, применяемой формы работы является гибкое сочетание самостоятельной учебной деятельности студентов с различными источниками информации, их оперативное и систематическое взаимодействия с преподавателями. В этом же плане применение синтеза традиционных методик с созданием оптимальной среды для учебного труда студентов может рассматриваться как средство оптимизации учебного процесса. Практика проведения занятий на основе групповой формы работы с сочетанием индивидуального подхода подтвердила широкие возможности коллективно-личностной деятельности в деле формирования профессиональных и социальных качеств личности студентов.
Ключевые слова: групповая форма работы с сочетанием индивидуального подхода, математические методы, моделирование, «дерево» решений, ожидаемый эффект решения.
METHOD FORMED WITHIN THE FRAMEWORK OF GROUP WORK COMBINED WITH INDIVIDUAL APPROACH
Research article
Akmatkulov A.A.1, *, Abakirova G.Zh.2, Mukhtarbekova R.M.3
1 ORCID: 0000-0002-5498-0281;
2 Kyrgyz National University named after Jusup Balasagyn, Bishkek, Kyrgyzstan;
1, 3 Kyrgyz State Technical University, Bishkek, Kyrgyzstan
* Corresponding author (aakmatkulov[at]inbox.ru)
AbstractThe article addresses the issues of teaching on the example of teaching methods of mathematical modeling in economics. It was confirmed that when applying for group work, the effectiveness of training depended on a complex of subjective factors determined by the volume of work and the attitude of students to practical activities. It was revealed that the group work form with a combination of an individual approach had a great influence on the motivation of learning activities. The undoubted advantage of this form of work was the flexible combination of students' independent learning activities with various sources of information, their prompt and systematic interaction with teachers. At the same time, the application of the synthesis of traditional methods with the creation of an optimal environment for students' academic work can be considered as a means of optimizing the educational process. The practice of conducting classes on the basis of a group form of work with a combination of an individual approach confirmed the wide possibilities of collective personal activities in the formation of the professional and social qualities of the students' personality.
Keywords: group work with a combination of an individual approach, mathematical methods, modeling, decision tree, expected effect of a decision.
Выбранную тему можно рассматривать с точки зрения определения потребностей и ожиданий студентов в области организации практики, с точки зрения пожеланий, высказываемых ими в адрес преподавателей, осуществляющих образовательный процесс. Насколько процесс обучения отвечает информационным основам избранной специальности, зависит и от отношения студентов к программе и содержанию преподаваемой дисциплины, методам ее реализации.
В педагогических трудах образовательный процесс значительно реже рассматривается с позиций студенчества. В конечном счете это сказывается на эффективности всей учебной работы высшей школы. Содержания учебно-воспитательной работы должно отвечать структуре процесса познания, обеспечивать лучшее усвоение познавательного опыта, оказывать более глубокое влияние на «становление профессионала» [9, С. 159-181]. Теперь подробнее охарактеризуем функции практических занятий с применением индивидуализации работ, с созданием у каждого студента более прочной установки на получение учебной информации, а это и явится предпосылкой возможности групповой работы по повышению интереса к изучаемым материалам.
Педагогическая наука рассматривает развитие личности не как пассивный продукт влияния среды и воспитательных воздействий, а наоборот огромное значение она придает активности самой личности, ее творческо-преобразующей деятельности, “в которой формируются такие качества как требовательность к себе, направленность на созидание результата и умение разумно организовать свой труд” [1, С. 57].
В нашей практике обучения, для студентов инженерно-экономического факультета, разрабатывается система заданий по математическим методам и моделированию в экономике, состоящая из 120 упражнений и задач на учебный семестр для второго курса. Система заданий составляется так, чтобы решение данной задачи или обучающие упражнения создавали предпосылку к решению следующих, более трудных производственных задач. Глубина и широта осмысления студентами, добытых ими самостоятельно знаний как качество их математической деятельности, реально должна стать целеполагающим компонентом профессионального образования.
«При этом важнейшей с психологической точки зрения является ориентировочная часть деятельности, выполняющая сигнальную функцию и ориентирующая индивида на процесс решения, в том числе учебных задач» [9, С. 62]. «Характерными признаками ориентировочной основы учебной деятельности являются ее неизменность на векторе цель результат и реальная возможность и эффективност исполнения деятельности
Во-первых, решение задач позволяет сделать знания студента осознанными, избавить их от формализма. Во-вторых, формирует у него научно теоретического типа мышления в отличие от интуитивного. «Механизмом осуществления деятельности является решение задач» [10, С. 49].
Значимость прикладных задач математики в профессиональном образовании неоднократно подчеркивали педагоги–математики: В.В. Давыдов [4], Л.М. Фридман [5], В.Г. Болтянский [8], В.Д. Шадриков [9], Е.И. Смирнов и др.[6]. Черты математической подготовленности, вляющие на научные мышления будущих специалистов, выразительно сформулировали в своих докладах участники Республиканской студенческой научно-технической конференции в городе Донецке, 24 апреля 2018 г.[7, Cекция II].
В самом деле, эти опытные педагогические результаты обусловлены основополагающими принципами построения и проведения практических занятий на основе проблемности с созданием соответствующих дидактических ситуаций. Для нас существенно важно, что организация работы в малых группах с сочетанием индивидуального подхода предполагает следующие положения эффективного обучения: мобильность, динамичность, проблемность, занимательность, коллективность, обратная связь и системность. Следовательно, мы видим центральную задачу вузовской дидактики в практическом обосновании принципов часто используемой технологии обучения и ее структурных элементов, в выявлении их внутреннего и внешнего взаимодействия.
Представим себе процесс обучения моделированию средствами «математических методов в экономике» студента, желающего, но не умеющего моделировать и решать – в сущности, мыслить и действовать в конкретной обстановке. Феномен моделирования состоит в том, что моделирующая деятельность студента строится на принципе проблемности и включает в себя элементы научной деятельности.
Как воплотить моделирующую деятельность в технологию обучения. Ответ прост - нужно создать среду для моделирования и решать поставленную задачу.
Например, при применении учебных пособий: «Математика в экономике» [2] и «Высшая математика для экономистов» [3], авторы стремились следовать тем методическим принципам, которые были положены в основу последних изданий этих учебников и получили одобрение других преподавателей. В течение первой половины семестра (модуль 1) студенты начального курса решают логические задачи на построение матрицы смежности и инцидентности графа (орграфа), простейшие задачи графического изображения принятия решений, в котором отражены альтернативные решения, состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды. Эти типы задач содержатся и в системах упражнений для второй половины семестра (модуль 2), но их сложность возрастает.
В первой половине семестра удобнее иметь карточки с текстом одного задания. Студент получает задание и выполняет его дома или в аудитории.
Во второй половине семестра нормой считается решение за неделю трех заданий. Наиболее трудные задачи разбираются на аудиторных занятиях. За каждую верно решенную задачу студент получает до 10 баллов, таким образом, семестр завершается успешно для каждого студента. Для каждого занятия ситуация выставления баллов как определенный стимул может быть выбрана по усмотрению преподавателя с учетом того, в чем больше достигли студенты в течение занятий по уровню и глубине, составленных моделей и от выбора ведущих переменных.
Для поддержания интереса студентов к решению задач необходимо было разнообразить этапы проведения практического занятия. 1. Обеспечение группы методическими указаниями по данной теме. 2.Организация занятия. 2. Формирование малых групп (3-5 чел.). 3. Регламент деятельности по сложности задачи. 4.Процесс решения задачи. 5. Подведение итогов занятия.
В конце второго модуля семестра студенту дается четыре задания на неделю. Каждое задание оценивается определенным количеством баллов, в зависимости от трудности. 2-3 задания посильны студенту средней успеваемости и предназначаются они для углубленного повторения теоретического материала и его сущности.
В ходе определения содержания того или иного раздела дисциплины не последнее место занимают вопросы, связанные с оценкой прикладной стороны задачного материала. Это приводит к интуитивной оценке информационно-практической емкости изучаемого раздела или вопросов курса.
Например, чтобы сформировать у студентов умение переводить текст задач на язык «дерева» решений, следует отработать сначала перевод отдельных элементов текста задачи и их связей на язык графов, а уж затем построение решения.
Задача
Южнокорейская госкомпания KEPCO рассматривает возможность строительства каскада малых ГЭС на реке Кара-Унгур. Если каскад из двух станций с общей мощностью 36 МВт в год будет работать стабильно, компания получит прибыль 60 млн. сом в год. При низкой производительности работы каскада компания может потерять 45 млн. сом. По данным экспертов существует 65% шансов, что каскад будет работать, но с низкой производительностью. Можно построить экспериментальную министанцию (ЭМС), а за тем уже решать, строить или нет каскад. Экспериментальная министанция обойдется в 3 млн. сом. Эксперты считают, что существуют 50% шансов, что министанция будет работать стабильно. Если экспериментальная министанция будет работать, то 95 % шансов за то, что построенный каскад также будет работать стабильно. Если же министанция не будет работать, то только 15% шансов за то, что каскад заработает стабильно. 1) Следует ли строить экспериментальную министанцию? 2) Следует ли построить каскад малых ГЭС? 3) Каков ожидаемый эффект наилучшего решения?
«Дерево» решений – это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив. Его применяют тогда, когда необходимо принимать последовательный ряд решений.
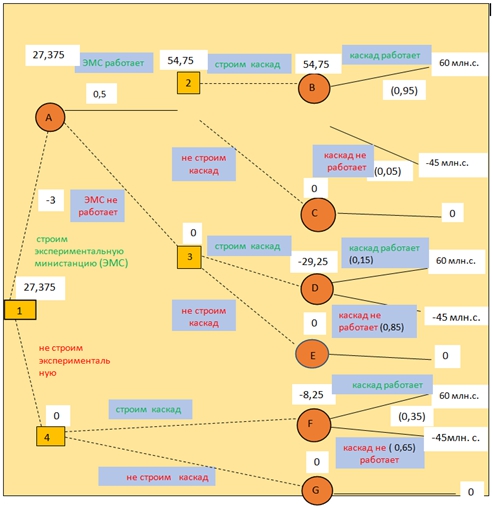
Строят «деревья» слева направо. Места, где принимаются решения, обозначают квадратами, места появления исходов – кругами, возможные решения пунктирными линиями, возможные исходы – сплошными линиями. Расходы, вызванные решением, проставляются на соответствующей ветви. (Рис.1).
По условию задачи, в узле F возможны исходы «каскад работает» с вероятностью 0,35 (что приносит прибыль 60 тыс.с.) и «каскад не работает» с вероятностью 0,65 ( что приносит убыток - 45 тыс.с.). Далее, для каждой альтернативы считаем ожидаемую эффективность (ОЭ) принятого решения – максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей:
ОЭ(F) = 0,35 ∙ 60 + 0,65 ∙ (-45) = 21 - 29,25 = - 8,25 млн.с.
Это число пишем над узлом F. (см. рис.1)
В узле 4 выбираем между решением «строим каскад» и «не строим каскад». Оценка этого решения ОЭ (G) = 0. Эту оценку мы пишем над узлом 4, а решение «строим каскад» отметили на дуге 4-F зеленым цветом.
Таким образом, в узле В возможны исходы:
ОЭ(В) = 0,95∙ 60 + 0,05 ∙ (-45) = 57 – 2,25 = 54,75. ОЭ(С) = 0.
Аналогично:
ОЭ(2) = max { ОЭ(В), ОЭ(С)} = max ( 54,75; 0 ) = 54,75 = ОЭ(В).
ОЭ(D) = 0,15 ∙ 60 + 0,85 ∙ (-45) = 9 – 38,25 = -29,25. ОЭ(Е) = 0.
ОЭ(3) = max { ОЭ(D), ОЭ(Е)} = max { -29,25; 0} = 0 = ОЭ(Е).
Рис.1 – Графическое изображение альтернативных решений
ОЭ(А) = 0,5 ∙ 54,75 + 0,5 ∙ 0 - 8,25 = 27,375.
ОЭ(1) = max {ОЭ(А), ОЭ(4)} = max {27,375; 0} = 27,375 = ОЭ (А).
И ожидаемый эффект решения ( минимальная затрата) 27,375 млн.с., то есть строим экспериментальную министанцию. Если министанция работает стабильно, то строим каскад. В случае не стабильной работы министанции, не строим каскад.
Как известно, основными компонентами любой экономической деятельности являются анализ проблемной ситуации, постановка экономической задачи, поиск ее решения, моделирование, исследование, прогнозирование, сравнение, оформление конечного результата и т.д. Каждый из этих компонентов в той или иной степени подразумевает процесс творчества, успех которого определяется широтой сферы поиска, интуицией, последовательностью логики, волей самих участников решения задач.
Поэтому сейчас необходимо стремиться не просто к повышению уровня усвоения знаний на основе деятельностного подхода к обучению, но и к отражению в его содержании общей методологии творческой деятельности экономиста, мотивация к которой должна формироваться уже на самых ранних этапах. Тем не менее проф. Атанов Г.А. из Донецка отмечает: «Если хочешь чему-нибудь научиться, то работай, а не учись» [10, С. 55].
В психологической науке установлено, что знаниям можно научиться только в процессе их использования в деятельности, только оперируя ими. «Надо начинать с дела. Учись (консультируйся, читай книги, лезь в Интернет) только тогда, когда ты не можешь сделать что-то конкретное, потому что не знаешь, как это делать, когда тебе надо получить ответ на конкретный вопрос. Вот когда появляется предметность. Нашел ответ – продолжай дело» [там же, С. 55]. Большинство занятий вызвали определенный эмоциональный подъем студентов.
Причины их заинтересованности и увлечения в том, что все предложенные задачи были реальными, студенты имели возможность изучить процессы количественных изменений в экономике, провести критический анализ существующих факторов и их взаимосвязи.
Основные трудности, которые встретились в обучении, сводятся к следующим: пришлось столкнуться с пассивностью отдельных обучаемых и искать приемы стимулирования их активности; в каждом конкретном случае приходилось выбирать особую стратегию руководства, участия или не участия в обсуждениях. Наибольший эффект, как показал опыт, дало применение дискуссий по каждой задаче с участием всей группы и дальнейшая проработка и развитие полученных коллективных идей с использованием других методов.
После завершения практических занятий весеннего семестра были проведены беседы со студентами и анкетный опрос. Подавляющее большинство студентов отметили, что форма проведения занятий интересна, позволила получить навыки моделирования в экономике.
Главную роль, по их мнению, сыграла в этом конкретность поставленных задач. Анонимная анкета, предъявленная студентам в конце семестра, также дала возможность получить интересные данные:
а) на младших курсах преобладающая часть студентов предпочитает чередование групповой и индивидуальной работы;
б) исключительно индивидуальную работу на занятих предпочитает только очень незначительное число студентов ( ок. 20%).
Применение компьютерных математических пакетов (MathCad, MathLab, Maple) в начальном периоде изучения дисциплины менее эффективно, поскольку сначала нужно подготовить каждого обучающегося к умению создать вычислительный алгоритм. Пока вопрос о передаче этого вида деятельности компьютерам не возник. Компьютерные математические системы должны создавать приемущества в смысле ускорения получения результатов или выполние рутинных операций и громоздких вычислений.
Проведенные работы в обучении позволили нам накопить полезный опыт проведения практических занятий по естественно-математическим дисциплинам и сделать следующие выводы: во-первых, проведение подобных занятий на I-II курсах может позволить совмещать обучение с эффективным решением реальных учебно-методических проблем; во-вторых, постановка в вузе практических занятий по курсу « Математические методы и моделирование» требует разносторонней обработки оптимальных частных методик организации учебного процесса в зависимости от направления подготовки.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Акматкулов А.А. Формирование критического отношения студента к результатам своей работы/ А.А.Акматкулов, Г.Ж.Абакирова, Г.А. Зикирова// Наука, техника и образование.-2017.-№ 11(41).- С. 53-57.
- Красс, М. С. Математика в экономике: математические методы и модели: учебник для СПО / М. С. Красс, Б. П. Чупрынов ;— 2-е изд., испр. и доп. - М. : Издательство Юрайт, 2017. — 541 с.
- Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. проф. H.Ш. Кремера. - 3-е изд. - М.: ЮНИТИ-ДАНА, 2010.-479 с.
- Давыдов В.В. Проблемы развивающего обучения: Опыт теоретического и экспериментального психологического исследования. – М.: Педагогика, 1986. – 240 с.
- Фридман Л.М. Наглядность и моделирование в обучении.- М.: Знание, 1984.-80 с.
- Смирнов Е. И. Технология наглядно-модельного обучения математике: Монография. Ярославль: ЯГПУ им. К. Д. Ушинского, 1998. – 335 с.
- Математическая культура инженера// Сборник докладов Республиканской студенческой научно-технической конференции, 24 апреля 2018 г., Донецк: Дон НТУ, 2018-. 277 с. [Электронный ресурс].URL:https://issuu.com/studtv.donntu/docs/ matematicheskaya_kultura_inzhenera.( дата обращения 25.09.2018).
- Болтянский В.Г. Математика: Лекции, задачи, решения:Учебное пособие [Текст] / В.Г.Болтянский, Ю.В.Сидоров,М.И.Шабунин – М.:Попурри,1996.-640 с.
- Подготовка учителя математики: Инновационные подходы: Учеб.пособие / Под ред. В.Д.Шадрикова.- М.:Гардарики, 2002.- 383 с.
- Атанов Г.А. Деятельностный подход в обучении[Электронный ресурс] /Модератор: Г.А. Атанов // Educational Technology &Society-. 2001.- N 4(4).-C.48-55-.URL: http://elibrary.lt/resursai/Uzsienio%20leidiniai/IEEE/Russian/ 2001/Nr%204/OTOpdf (дата обращения 01.10.2018).
Список литературы на английском языке / References in English
- Akmatkulov A.A. Formirovaniye kriticheskogo otnosheniya studenta k rezul'tatam svoyey raboty [Formation of the student’s critical attitude towards the results of their work] A.A.Akmatkulov, G.ZH.Abakirova, G.A. Zikirova// Nauka, tekhnika i obrazovaniye. Nauchno metodicheskiy zhurnal [Science, technology and education. Scientific Methodical journal].-2017.--№ 11(41).- P. 53-57. [in Russian]
- Krass, M. S. Matematika v ekonomike: matematicheskiye metody i modeli: uchebnik dlya SPO [Mathematics in economics: mathematical methods and models: a textbook for SPO] M. S. Krass, B. P. Chuprynov ; pod red. M. S. Krassa. — 2-ye izd., ispr. i dop. — M. : Izdatel'stvo Yurayt,[ M.S. Krass, B.P. Chuprynov; by ed. M.S. Crassus. - 2nd ed., Corr. and add. - M.: Yurait Publishing House] 2017. — 541.[in Russian]
- Vysshaya matematika dlya ekonomistov: uchebnik dlya studentov vuzov, obuchayushchikhsya po ekonomicheskim spetsial'nostyam[Higher mathematics for economists: a textbook for university students enrolled in economic specialties] / [N.SH. Kremer i dr.]; pod red. prof. H.SH. Kremera. - 3-ye izd. - M.: YUNITI-DANA,2010 [[N.Sh. Kremer et al.]; by ed. prof. H.Sh. Kremer. - 3rd ed. - M .: UNITY-DANA,2010]]. – P.479. [in Russian]
- Davydov V.V. Problemy razvivayushchego obucheniya [Problems of developmental education ] M.,1986. – 240 . [in Russian]
- M. Fridman. Naglyadnost' i modelirovaniye v obuchenii,[Visualization and modeling in training] М.: Znanie.,1984. – P. 80 . [in Russian]
- Smirnov E. I. Tekhnologiya naglyadno-model'nogo obucheniya matematike: Monografiya. Yaroslavl'[Smirnov EI. Technology of visual-model education in mathematics: Monograph. Yaroslav]: YAGPU im. K. D. Ushinskogo, 1998. – 335. [in Russian].
- Matematicheskaya kul'tura inzhenera // Sbornik dokladov Respublikanskoy studencheskoy nauchno-tekhnicheskoy konferentsii,[Mathematical culture of an engineer // Collection of reports of the Republican Student Scientific and Technical Conference] 24 aprelya 2018 g., Donetsk: DonNTU, 2018 -. P.277. [Elektronnyi resurs]. (the date of circulation is 09/25/2018) [in Russian]. ( URL:https://issuu.com/studtv.donntu/docs/ matematicheskaya_kultura_inzhenera. [in Russian].
- Boltyanskiy V.G. Matematika: Lektsii, zadachi, resheniya:Uchebnoye posobiye [ Tekst][ Mathematics: Lectures, tasks, solutions: Tutorial]/ V.G.Boltyanskiy, YU.V.Sidorov,M.I.Shabunin – M.:Popurri, 1996.- P.640 . [in Russian]
- Podgotovka uchitelya matematiki: Innovatsionnyye podkhody: Ucheb.posobiye [Mathematics teacher training: Innovative approaches: Textbook]/ Pod red. V.D.Shadrikova.- M.:Gardariki, 2002.- 383 . [in Russian]
- Deyatel'nostnyy podkhod v obuchenii [Activity approach in training]. [еlectronic resource] / Moderator: G.A. Atanov // Educational Technology & Society-. 2001.- N 4 (4) .- C.48-55-.URL: URL:http://elibrary.lt/resursai/Uzsienio%20leidiniai/IEEE/Russian/ 2001/Nr%204/OTO_2001_4_01.pdf.]. (accessed:01.102018).[in Russian]