ИСПОЛЬЗОВАНИЕ ИНТЕРАКТИВНОЙ ГЕОМЕТРИЧЕСКОЙ СРЕДЫ GEOGEBRA В ВУЗОВСКОМ КУРСЕ МАТЕМАТИКИ
Ерилова Е.Н.
Старший преподаватель кафедры математики, Северный Арктический Федеральный Университет имени М.В. Ломоносова
ИСПОЛЬЗОВАНИЕ ИНТЕРАКТИВНОЙ ГЕОМЕТРИЧЕСКОЙ СРЕДЫ GEOGEBRA В ВУЗОВСКОМ КУРСЕ МАТЕМАТИКИ
Аннотация
В статье рассмотрены возможности отдельных программных продуктов профессионального и образовательного назначения, перечислены достоинства интерактивной геометрической среды GeoGebra, а также приведен пример её использования в процессе изучения вузовского курса математики.
Ключевые слова: интерактивная геометрическая среда GeoGebra, программные продукты.
Erilova E.N.
Senior lecturer of department of mathematics, Northern (Arctic) Federal University named after M.V. Lomonosov
THE USE OF THE INTERACTIVE GEOMETRY TOOL GEOGEBRA IN A HIGH SCHOOL COURSE OF MATHEMATICS
Abstract
The article describes the capabilities of some software products for professional and educational purposes, lists the advantages of the interactive geometry tool GeoGebra, and also gives an example of its use in the process of learning high school mathematics course.
Keywords: the interactive geometry tool GeoGebra, software products.
В последние годы в процессе преподавания различных дисциплин в вузе всё чаще используются программные продукты, как профессионального, так и образовательного назначения. Особенно актуальным стало использование различных пакетов программ в ходе изучения математических дисциплин.
Существует достаточно большое количество программных продуктов, способствующих активизации образовательного процесса. Например, такие программы, как: Maple, Mathcad, Mathematica, MatLAB, GeoGebra, GeoNext, C.a.R.и др. Применение программных средств особенно актуально на занятиях по высшей математике. Вышеперечисленные пакеты программ способствуют выполнению расчетов за короткое время, позволяют выполнять построения графиков функций и объемных тел и т.д.
Более подробно остановимся на применении интерактивной геометрической среды GeoGebra при изучении курса высшей математики. GeoGebra — бесплатная программа, которая даёт возможность создания динамических чертежей для использования на разных уровнях обучения геометрии, алгебры, планиметрии и других смежных дисциплин. Программа позволяет работать с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.). Идея GeoGebra заключается в интерактивном сочетании геометрического, алгебраического и числового представления. Можно создавать конструкции с точками, векторами, линиями, коническими сечениями, а также математическими функциями, а затем динамически изменять их. [1, c.495]
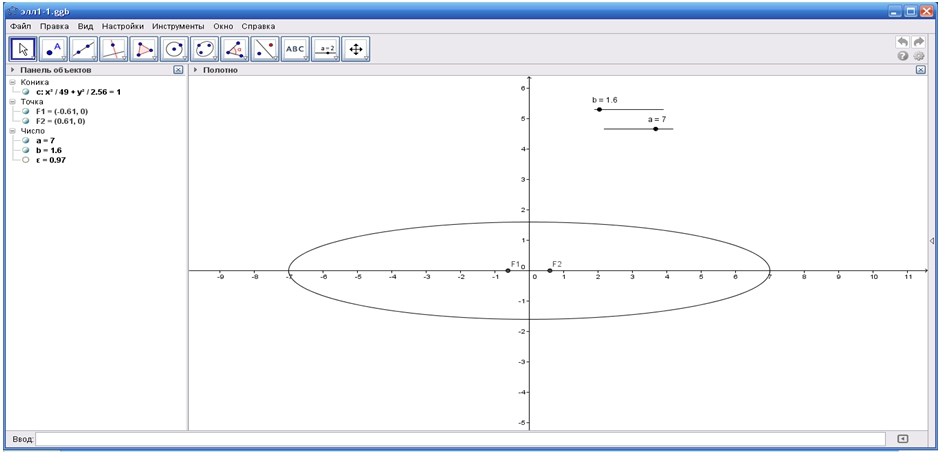
Использование интерактивной геометрической среды GeoGebra актуально при изучении таких разделов вузовского курса математики, в которых помимо вычислений необходимо выполнять и геометрические построения изучаемых математических объектов. Так, например, в процессе изучения темы «Кривые второго порядка» выполняются геометрические построения следующих кривых: эллипса, гиперболы, параболы. А также рассматриваются различные формы этих кривых и их расположение на координатной плоскости в зависимости от заданного уравнения. Используя динамичность образов создаваемых с использованием программы GeoGebra, можно показать обучающимся изменение формы эллипса в зависимости от отношения его большой и малой полуосей (a и b). На рисунке 1 изображен эллипс для случая, когда его большая ось лежит на оси Ox, т.е. a>b.
Рис.1
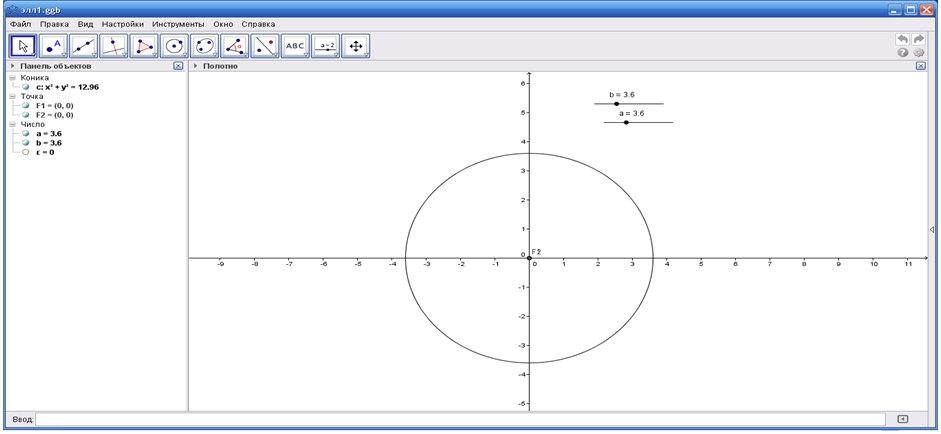
Используя динамичность созданного образа, добьемся равенства большой и малой полуосей эллипса, т.е. a=b. График эллипса, как показано на рисунке 2, преобразуется в окружность.
Рис.2
Аналогично, рассматривают форму эллипса и для случая a<b.
В процессе изучения гиперболы и параболы, а также при решении задач с участием кривых второго порядка можно использовать интерактивную геометрическую среду GeoGebra. Рассмотрим решение задачи 4.3.78. из "Сборника задач по высшей математике" автора Лунгу К.Н. и др.
Задача 4.3.78. Найти площадь треугольника, образованного асимптотами гиперболы ![]() и прямой
и прямой ![]() . [2, c. 161].
. [2, c. 161].
Решение этой задачи выполним, используя программу GeoGebra. Построим гиперболу и её асимптоты, затем заданную прямую ![]() . Таким образом, получаем треугольник
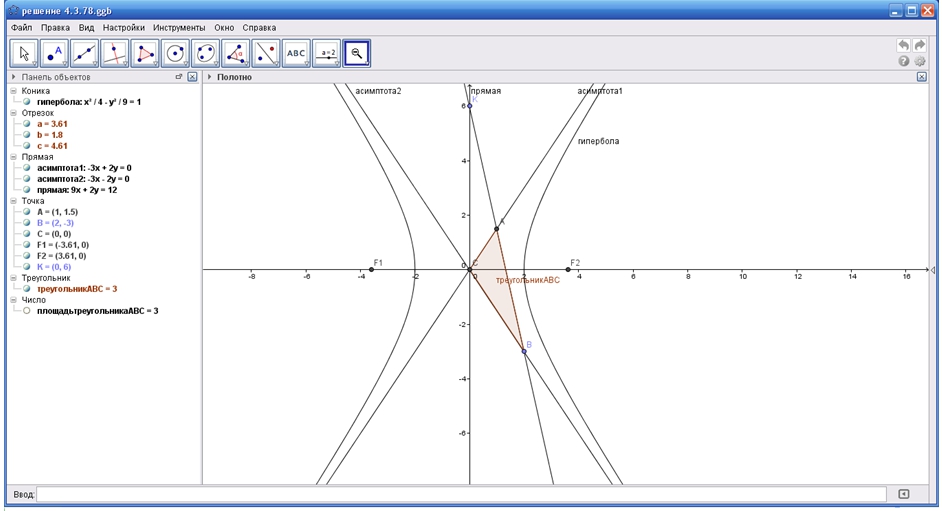
. Таким образом, получаем треугольник ![]() , после чего находим его площадь. Построение треугольника, а также все вычисления, полученные в процессе решения задачи, показаны на рисунке 3.
, после чего находим его площадь. Построение треугольника, а также все вычисления, полученные в процессе решения задачи, показаны на рисунке 3.
Рис.3
Применение интерактивной геометрической среды GeoGebra в ходе решения задач, а также при изучении лекционного материала позволяет выполнить наглядное изображение всех изучаемых математических объектов, что способствует лучшему пониманию нового материала, ускоряет процесс решения задач, упрощает вычислении и т.д.
Литература
- Идея укрупнения дидактических единиц в вузовском курсе математики //Теоретические и прикладные аспекты математики, информатики и образования. Материалы Международной научной конференции. Архангельск, 16-21 ноября 2014г. Архангельск: САФУ, 2014. С. 493-497.
- Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. - 2-е изд., испр.- М.: Айрис-пресс, 2003. — 576 с.
References
- Erilova E. Ideja ukrupnenija didakticheskih edinic v vuzovskom kurse matematiki //Teoreticheskie i prikladnye aspekty matematiki, informatik i obrazovanija. Materialy Mezhdunarodnoj nauchnoj konferencii. Arhangel'sk, 16-21 nojabrja 2014g. Arhangel'sk: SAFU, 2014. S. 493-497.
- Lungu K.N., Pis'mennyj D.T., Fedin S.N., Shevchenko Ju.A. Sbornik zadach po vysshej matematike. 1 kurs. - 2-e izd., ispr.- M.: Ajris-press, 2003. — 576 s.