Determination of vertical gradient of gravity anomalies by numerical differentiation method
Determination of vertical gradient of gravity anomalies by numerical differentiation method
Abstract
The article examines a fairly simple method of calculating the vertical gradient of gravity anomalies (VGGA), based on the use of the formula of numerical differentiation of gravity anomalies. The results of comparing the values of VGGA obtained by the method of numerical differentiation of gravity anomalies with the values of the vertical gradient of gravity anomalies calculated by the method of expansion in a series of spherical functions, which uses a set of harmonic coefficients of the global model of geopotential EIGEN-6C4, up to the degree N=2190 have been analysed. It is shown that the standard deviation obtained as a result of comparison of these methods was 0.13 E. Thus, the method of calculating the VGGA based on the use of formulas for numerical differentiation of force anomalies is not inferior in accuracy to the analytical method using the spherical function series expansion, which uses a set of harmonic coefficients of the global geopotential model EIGEN-6C4, up to degree N=2190.
1. Введение
Вопрос о способах вычисления вертикального градиента аномалий силы тяжести (ВГАСТ) имеет большое практическое значение, поскольку его использование значительно расширяет возможности геологической интерпретации результатов гравиметрической съемки, а также для геодезических целей, где вертикальный градиент аномалий силы тяжести входит в формулы первого приближения теории Молоденского , .
При получении числовых значении ВГАСТ по заданному распределению, аномалий силы тяжести на плоскости наблюдений обычно используются различные схемы вычислений, вытекающие из формулы Нумерова , которая имеет следующий вид:
где
– аномалия силы тяжести в исследуемой точке;
– аномалия силы тяжести в текущей точке на плоскости;
r, a – ее полярные координаты;
ось z направлена вертикально вниз.
Определение ВГАСТ на физической поверхности Земли по аномалиям силы тяжести, заданным на ее поверхности, с помощью формулы (1) возможно только в равнинных районах. В работах , для вычисления по формуле (1) предложены различные вычислительные схемы и палетки. Однако авторы не учитывают влияния отклонения физической поверхности Земли от отсчетной плоскости. В работе приведены результаты исследования точности формулы (1) на различных моделях, схематически представляющих формы рельефа, которые показали, что применение этой формулы при определении фигуры Земли и элементов ее гравитационного поля с относительной погрешностью порядка квадрата сжатия неудовлетворительно .
Существует ряд методов вычисления значений ВГАСТ , , , в которых учитывается реальная физическая поверхность Земли и оценивается влияние наклонов местности. Однако, в процессе вычисления с помощью приведенных в этих работах формулах, необходимо предварительно получить поправку первого приближения теории Молоденского – G1 и затем, с помощью этой поправки исправить аномалии силы тяжести в формуле (1) как . В результате, используя исправленные аномалии силы тяжести
, при вычислении по формуле (1), получают вертикальный градиент аномалии силы тяжести в первом приближении. При этом неоднократное использование методов численного интегрирования физической поверхности Земли может обесценить искомый результат. Кроме того, следует отметить, что при вычислении интеграла в формуле (1) на отсчетной плоскости z = 0 при
подынтегральное выражение на поверхности наблюдения обращается в бесконечность. Поэтому значения ВГАСТ при r = 0 на отсчетной поверхности z = 0 не могут быть вычислены.
В данной работе предлагается достаточно простой метод вычисления ВГАСТ, основанный на использовании формул численного дифференцирования . Численное дифференцирование применяется, когда исследуемую функцию невозможно продифференцировать аналитически, например, когда она задана таблично или в виде цифровой модели физического поля.
2. Основные результаты
Метод численного дифференцирования заключается в том, что бесконечно малые приращения функций и аргументов исследуемой функции заменяются отношением конечных разностей. Причем, чем меньше будет приращение аргумента, тем точнее численное значение производной.
Для вычисления ВГАСТ методом численного дифференцирования используется значение аномалии силы тяжести в двух точках. Приращение аргумента вычисления производных задается путем пересчета аномалий силы тяжести вверх по оси OZ на величину Δz от исследуемой точки. Это соответствует использованию конечноразностной схеме двухточечного шаблона численного дифференцирования, суть которого заключается в том, что на отсчетной плоскости OXZ в начале прямоугольных координат P(0,0,0) задана аномалия силы тяжести Δg(0,0,0), дифференцируемая достаточное число раз. Исходя из определения первой производной как
можно получить значение ВГАСТ в точке P(0,0,0) на плоскости z = 0 по следующей формуле
где
Δz>0 – малый параметр (шаг по высоте над плоскостью z = 0).
В этом случае земную поверхность в окрестности точки P(0,0,0) можно принять за горизонтальную плоскость. Причем достаточно иметь эту поверхность плоской в окружности радиуса 6H (H – отметка высоты центра этой окружности). Тогда пренебрежение влиянием внешней области на окрестность точки P(0,0,0) составить 12 км.
Для определения ВГАСТ, необходимого для решения задачи Молоденского с точностью первого приближения, характеристики глобального поля силы тяжести удобно представлять в системе сферических координат . В этом случае формулу (3) для вычисления ВГАСТ методом численного дифференцирования запишем в следующем виде
где
Δgs(P) – аномалия силы тяжести, вычисленная в точке ;
Δgs(P`) – аномалия силы тяжести, вычисленная в точке ;
r – радиус-вектор точки ;
и
– геоцентрическая широта и долгота точки
.
При вычислении ВГАСТ по формуле (4) использованы значения аномалий силы тяжести, полученные из разложения в ряд по сферическим функциям потенциала силы тяжести
где
– геоцентрическая гравитационная постоянная;
N – предельная степень разложения;
ae – экваториальный радиус Земли;
r = R + H – радиус-вектор точек на земной поверхности;
R – средний радиус Земли;
H – высота точки P;
– разность нормированных коэффициентов сферических функций реального и нормального поля силы тяжести;
– нормированные гармонические коэффициенты нормального геопотенциала, отнесенного к эллипсоиду WGS- 84, где
.
На рисунке 1 приведена картосхема – аномалий силы тяжести, вычисленных в точках
по формуле (5) , в которой использован набор гармонических коэффициентов глобальной модели геопотенциала EIGEN-6C4 до степени N = 2190 .
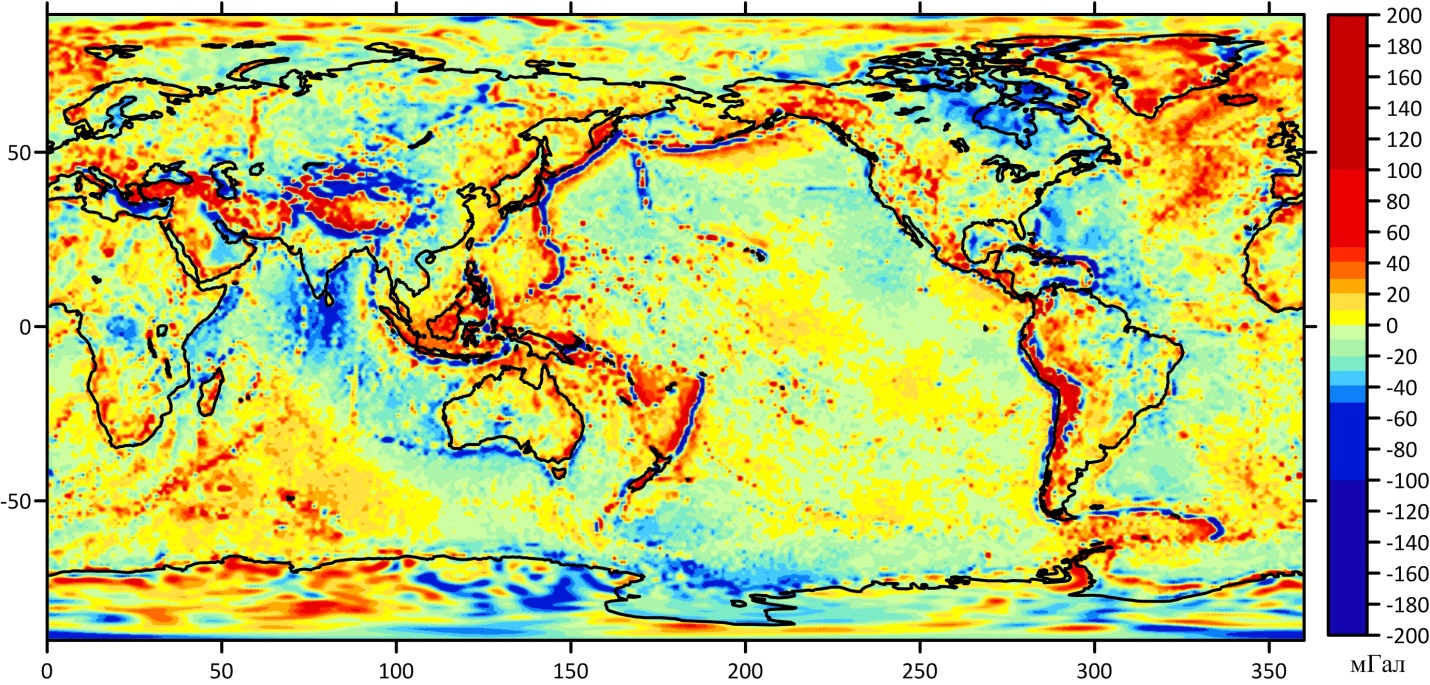
Рисунок 1 - Картосхема аномалий силы тяжести Δgs(P), вычисленных при Δr=0 по формуле (5) с учетом гармоник гнопотенциала до степени N=2190
На рисунке 2 представлена картосхема значений ВГАСТ, вычисленных по формуле численного дифференцирования аномалий силы тяжести (4), в которой использованы значения аномалий силы тяжести и
, вычисленные по формуле (5) при
и при
соответственно.
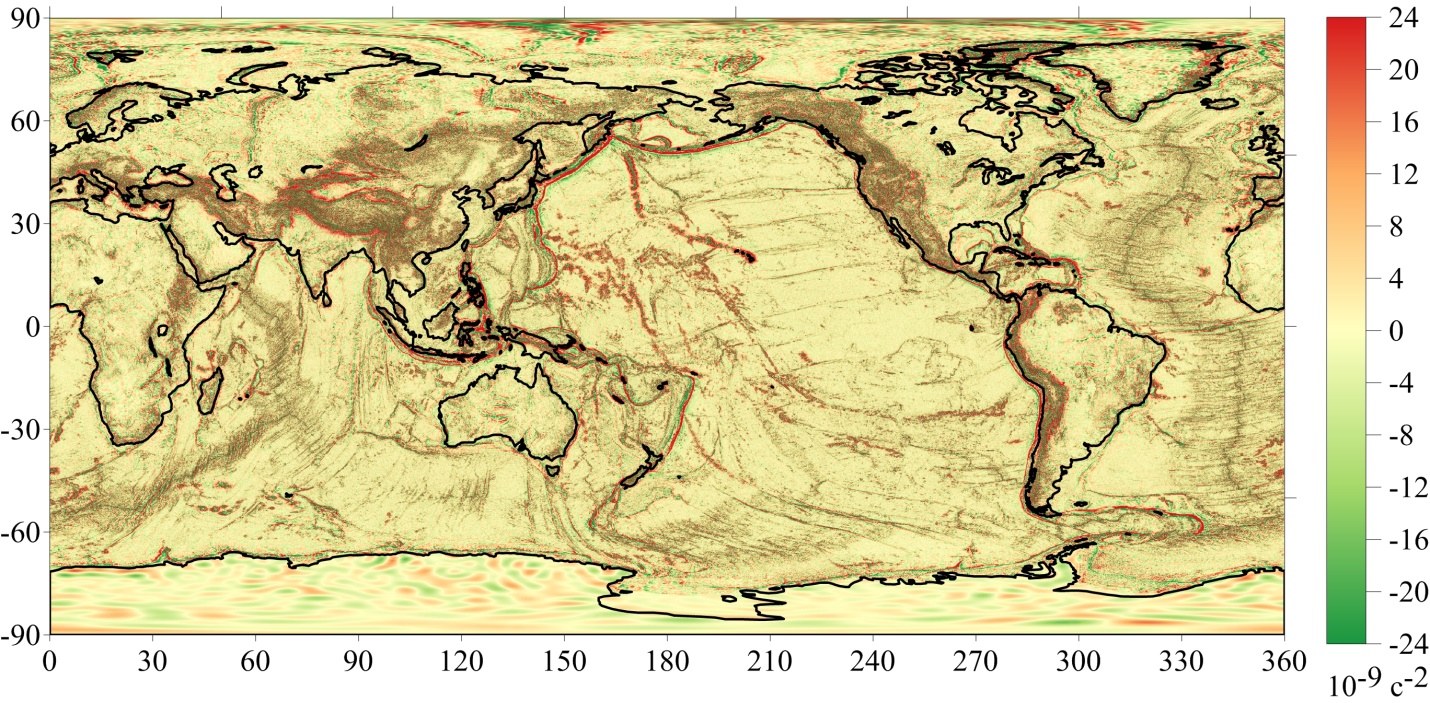
Рисунок 2 - Картосхема значений ВГАСТ, полученных по формуле (4)
Примечание: фрагмент диапазона шкалы изменения ограничен интервалом от -24∙10-9с-2 до +24∙10-9с-2
Причем в горных областях значения ВГАСТ весьма значительны. Кроме того, в настоящей работе выполнено определение ВГАСТ аналитически с помощью разложения в ограниченный ряд по сферическим функциям, в котором использованы гармонические коэффициенты глобальной модели геопотенциала EIGEN-6C4 до степени N=2190:
где ;
– нормированные гармонические коэффициенты геопотенциала;
– нормированные гармонические коэффициенты нормального геопотенциала, отнесенного к эллипсоиду WGS- 84;
– нормированные присоединенные функции Лежандра степени n и порядка m;
– геоцентрическая гравитационная постоянная;
ae – большая полуось эллипсоида;
r – геоцентрический радиус-вектор;
– геоцентрическая широта;
– географическая долгота;
T – аномальный потенциал силы тяжести.
На рисунке 3 приведена картосхема ВГАСТ, вычисленного по формуле (6) .
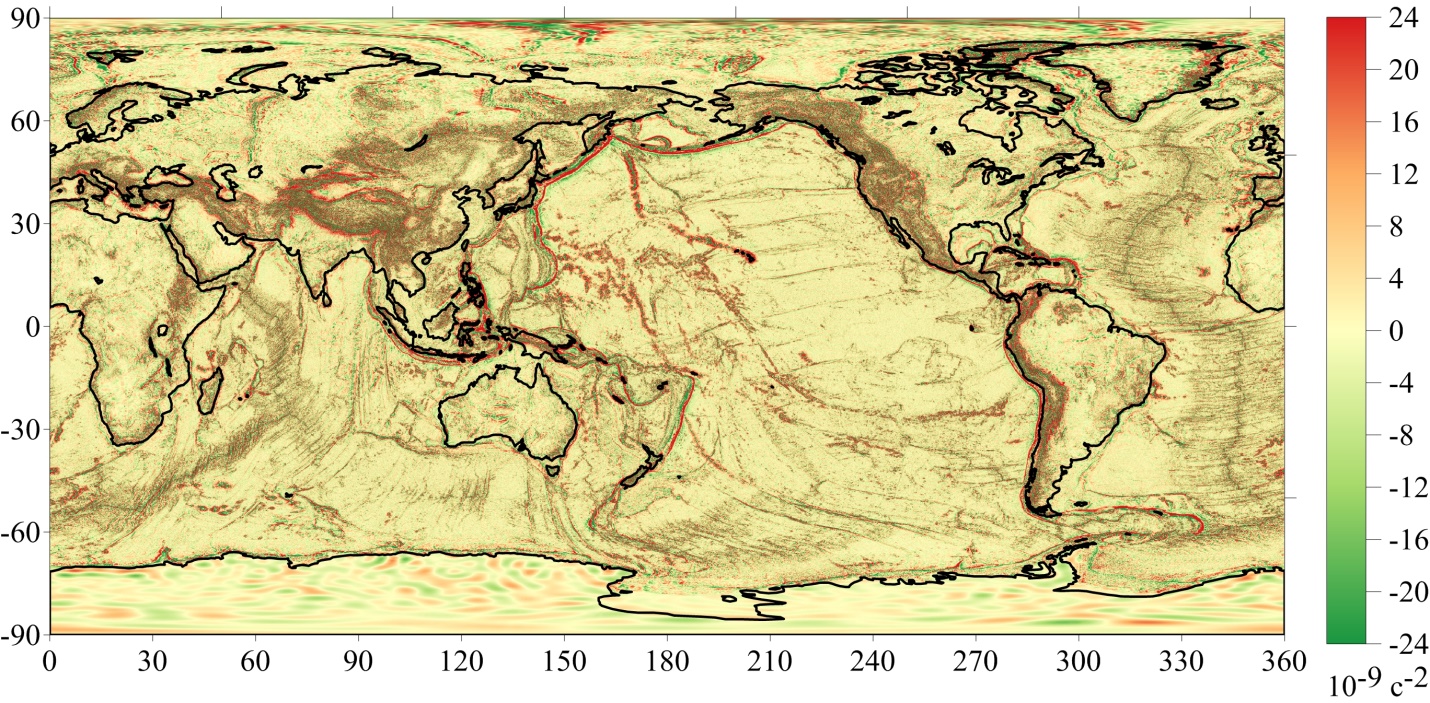
Рисунок 3 - Картосхема ВГАСТ, вычисленного по формуле (6)
Примечание: Фрагмент диапазона шкалы изменения ограничен интервалом от -24∙10-9с-2 до + 24∙10-9с-2
Разности ΔG(P) между значениями ВГАСТ, вычисленными по формулам (4) и (6), получены по формуле
На рисунке 4 показана картосхема распределения разности ΔG(P) между значениями ВГАСТ для территории земного шара.
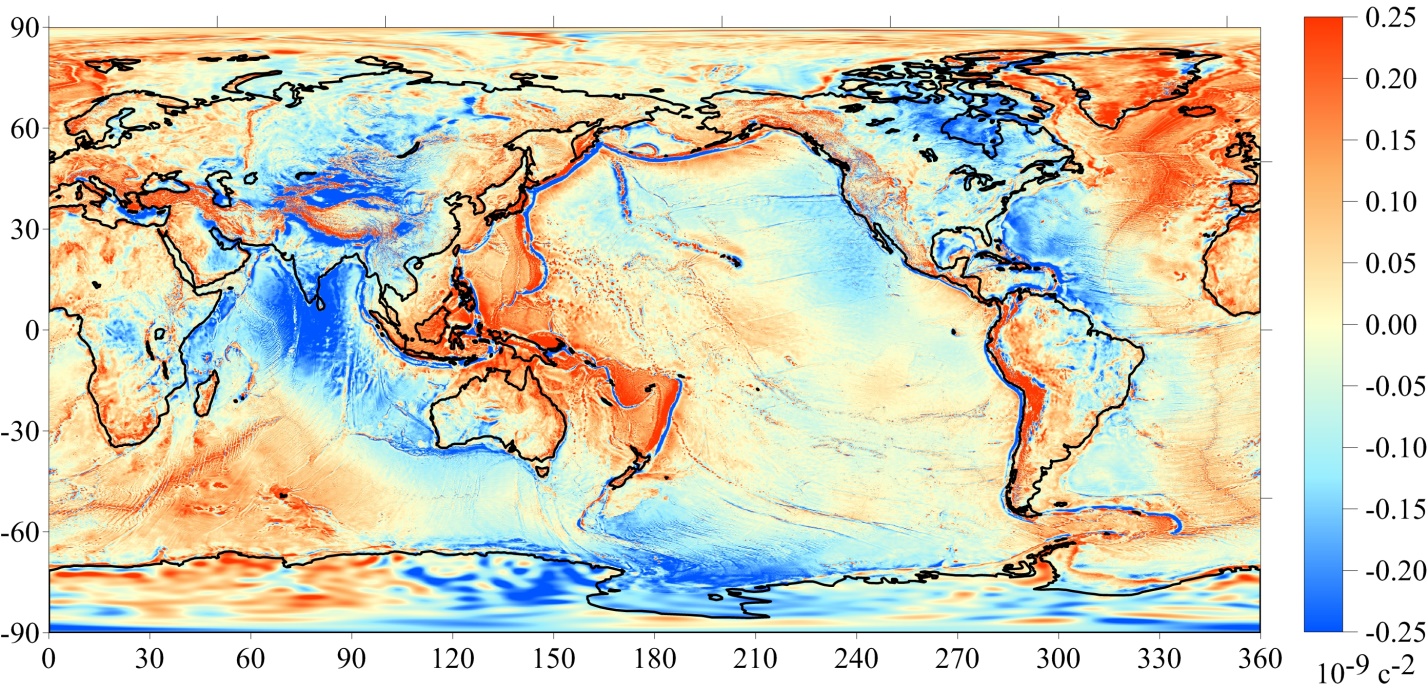
Рисунок 4 - Картосхема разности ΔG(P) между значениями ВГАСТ, вычисленными по формулам (4) и (6)
Статистическую картину распределения значений ΔG(P) на земной поверхности дает гистограмма, приведенная на рисунке 5.
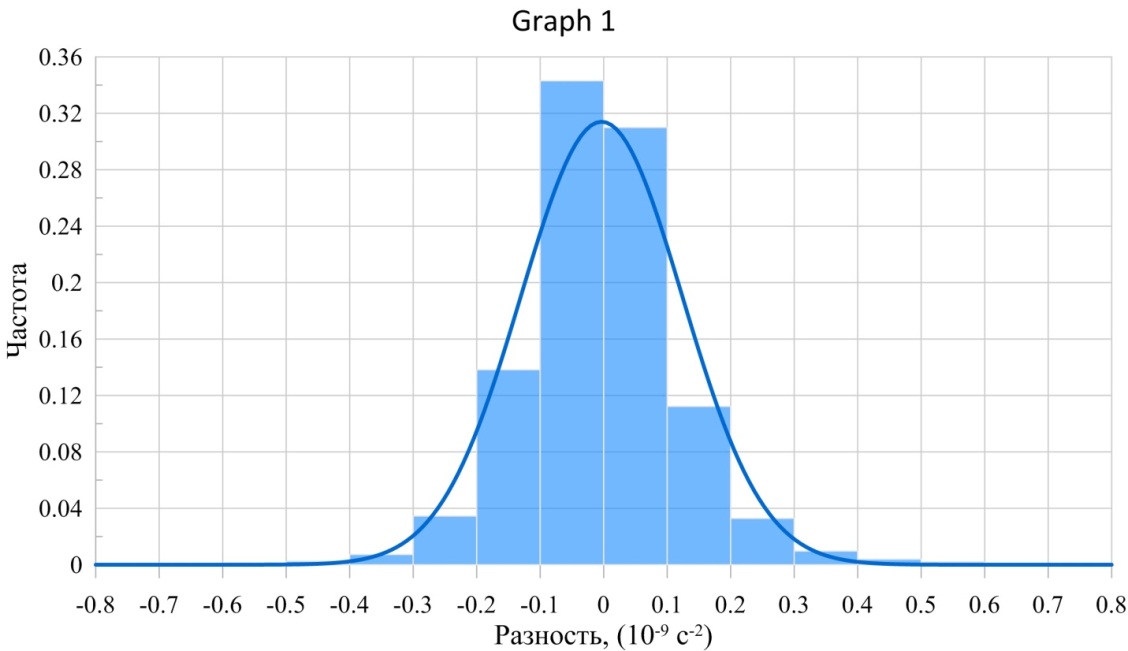
Рисунок 5 - Гистограмма распределения на земной поверхности разности ΔG(P)
В табл. 1 приведены статистические характеристики распределения разности ΔG(P) на территории земного шара.
Таблица 1 - Статистические характеристики распределения разности ΔG(P)
Характеристики | Значения |
Number of values | 9331200 |
Minimum (1∙10-9с-2) | -1,472 |
Maximum (1∙10-9с-2) | 2,273 |
Range (1∙10-9с-2) | 3,746 |
Mean (1∙10-9с-2) | -0,003 |
Standard deviation (1∙10-9с-2) | 0,129 |
Skew | 0,445 |
Kurtosis | 5,377 |
Critical K-S stat, a =.10 | <0,001 |
Critical K-S stat, a =.05 | <0,001 |
Critical K-S stat, a =.01 | 0,001 |
Из таблицы 1 видно, что максимальное абсолютное значение разности ΔG(P) равно 2,27∙10-9с-2, среднее арифметическое значение этой разности равно 0,003∙10-9с-2, а стандартное отклонение составляет = 0,1295∙10-9с-2.
3. Заключение
В работе проведен анализ результатов сравнения значений ВГАСТ, полученных методом численного дифференцирования аномалий силы тяжести со значениями вертикального градиента аномалий силы тяжести, вычисленных методом разложения в ряд по сферическим функциям, в котором использован набор гармонических коэффициентов глобальной модели геопотенциала EIGEN-6C4 до степени N=2190. Выполненные исследования позволяют сделать следующие выводы.
1. Вычисленные с помощью разложения в ряд по сферическим функциям значения ВГАСТ практически не отличаются от значений ВГАСТ, вычисленных по формуле численного дифференцирования. Максимальные расхождения между значениями ВГАСТ, вычисленными по данным глобальной модели геопоенциала EIGEN-6C4, при учете гармоник до 2190 степени, и вычисленным с помощью формулы численного дифференцирования, используя метод пересчета исходного поля на высоту 1 метр равно 2,27∙10-9с-2. Показано, что стандартное отклонение, полученное в результате сравнения этих методов, составило 0,13 Э.
2. Анализируя распределение результатов сравнения глобальных ВГАСТ, вычисленных по формулам (4) и (6), можно сделать вывод о возможности их использования для построения глобальной модели квазигеоида с точностью первого приближения теории Молоденского в ньютоновском приближении, где вертикальный градиент необходимо знать с относительной погрешностью порядка квадрата сжатия.
Таким образом, метод вычисления ВГАСТ, основанный на использовании формул численного дифференцирования аномалий силы не уступает по точности аналитическому методу с помощью разложения в ряд по сферическим функциям, в котором использован набор гармонических коэффициентов глобальной модели геопотенциала EIGEN-6C4, до степени N=2190.
