РЕШЕНИЕ ДУОПОЛИИ КУРНО ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО ПАРАМЕТРА ВРЕМЕНИ
РЕШЕНИЕ ДУОПОЛИИ КУРНО ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО ПАРАМЕТРА ВРЕМЕНИ
Научная статья
Дорофеева Ю.А.*
ORCID: 0000-0002-9327-6705,
Петрозаводский государственный университет, Петрозаводск, Россия
* Корреспондирующий автор (julana2008[at]yandex.ru)
АннотацияМодель дуополии предполагает действие на рынке только двух фирм, при этом каждая из них принимает цену и объем производства конкурента неизменными, и только после этого принимает собственное решение о следующем шаге на рынке. Каждый из двух игроков допускает, что его конкурент всегда будет удерживать свой выпуск стабильным. В классической постановке дуополии Курно определяется равновесие по цене, то есть оптимальную цену для обеих фирм-конкурентов, при которой они получат максимальную прибыль. В данной постановке, в отличие от классической модели, будет рассмотрена задача поиска оптимального решения для времени продаж.
Ключевые слова: теория игр, конкуренция, дуополия, равновесие Нэша, олигополия, рынок, некооперированная игра, модель Курно, объем производства, цена, модель Бертрана.
SOLUTION OF COURNOT DUOPOLY EQUILIBRUM TO DETERMINE THE BEST TIME PARAMETER
Research article
Dorofeeva Yu.A.*
ORCID: 0000-0002-9327-6705,
Petrozavodsk State University, Petrozavodsk, Russia
* Corresponding author (julana2008[at]yandex.ru)
AbstractThe duopoly model assumes that only two companies operate in the market. Each of them takes the price and volume of the competitor’s production as something permanent and makes its own decision about the next step at the market based on this information. Each of the two players assumes that the competitor will always keep the release at the same level. In the classical formulation of the Cournot duopoly, equilibrium is determined by price, that is, the best price for both competing companies that allows them to receive the maximum profit. This formulation considers the search for the best solution for the sales time in contrast to the classical model.
Keywords: game theory, competition, duopoly, Nash equilibrium, oligopoly, market, uncooperated game, Cournot model, production volume, price, Bertrand model.
ВведениеДуополия – частный случай олигополии, это та ситуация, при которой на рынке существует всего две компании, выпускающие подобную продукцию. Важно, что фирмы не связаны монополистической договорённостью о цене, рынках сбыта и квотах. Дуополия Курно – это модель равновесия в некооперированной олигополии, при условии, что такие параметры, как цена на свою продукцию и объём своего производства изменяются редко [3]. На рынке действуют только две фирмы, каждая из них отслеживает цену и объем производства конкурента, и только после анализа этих данных принимает собственное решение. Надо отметить, что в силу «стационарности» цены и объёмов производства данную модель можно применить к стабильным компаниям. В отличие от классических статистических прогнозов, дуополии интересны тем, что в этих постановка учитывается конфликт интересов. Прибыль, получаемая фирмой, зависит еще и от решений конкурента, который, в свою очередь, заинтересован максимизировать свою прибыль.
В классических постановках дуополии Курно решается задача поиска оптимальной цены продажи, иногда объема продаж. Интерес представляет вопрос об оптимальном времени продаж, не используя методы статистического прогнозирования.
Постановка задачи
Рассмотрим две фирмы, производящие похожую по цене и качеству сувенирную продукцию, действующих на территории г. Петрозаводска, Республики Карелия. Обе фирмы собираются предложить свою схожую продукцию покупателям, планируя определенный выпуск товара, и находятся в ожидании старта продаж. Допустим, что каждая из них считает, что стоимость единицы товара конкурента и соответствующий объем его продукции неизменными. Затем принимает решение относительно своего объема производства, его затрат, качества материалов с учетом того, что конкурент всегда будет удерживать свой выпуск стабильным. Задача состоит в поиске оптимального момента времени для получения наилучшей прибыли обеими компаниями, учитывая конкуренцию.
В качестве дополнительного исследования требуется найти оптимальную цену при реализации единицы товара сувениров для каждого из конкурентов с помощью дуополии Бертрана.
Реализация решения
Для решения этой задачи нам необходимо проанализировать данные компаний 1 и 2 по следующим финансовым показателям: доходы компаний, их прибыль, расходы, средняя стоимость продукта, рыночный спрос.
Посчитав и проанализировав издержки двух фирм, по финансовым данным был проведен подсчет объема продаж. По имеющемуся дискретному набору значений финансовых показателей издержек за 4 квартала 2019 года с применением метода интерполяции полиномом Лагранжа с помощью программы Wolfram Mathematica, была получена зависимость издержек от времени. Издержки каждой компании за четыре квартала 2018 и 2019 годов рассчитываются следующим способом:
![]() = операционные расходы компании за один квартал + другие расходы + налоги.
= операционные расходы компании за один квартал + другие расходы + налоги.
В результате, зависящие от времени t издержки 1 и 2 компаний:
![]()
Для всей линейки сувенирной продукции каждой из фирм определена средняя рыночная стоимость товаров: для компании 1 средняя стоимость ![]() , для компании 2-
, для компании 2-![]() руб.
руб.
Прибыль U1 компании 1 и прибыль U2 компании 2 в зависимости от соответствующих объемов выпускаемой продукции ![]() , в соответствии с [2], [3] вычисляются по формулам:
, в соответствии с [2], [3] вычисляются по формулам:
![]()
Каждая фирма стремится к наибольшей прибыли. В данном случае это и будет равновесие по Нэшу, определенное по времени. Для того чтобы найти максимум функции, найдем частные производные по переменным ![]() , и приравнивая их к нулю, найдем оптимальную величину времени:
, и приравнивая их к нулю, найдем оптимальную величину времени:
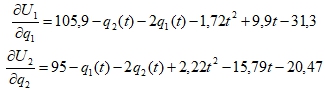
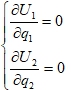 Решая систему:
Решая систему:
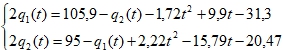 В результате получены выражения:
В результате получены выражения:
Данные функции изображены на рис.1.
Найдём точки пересечения графиков функций ![]() , которые определяют равновесие Нэша для конкурентов:
, которые определяют равновесие Нэша для конкурентов: ![]()
На рис. 1 выделена точка равновесия, соответствующая оптимальной величине времени продаж.
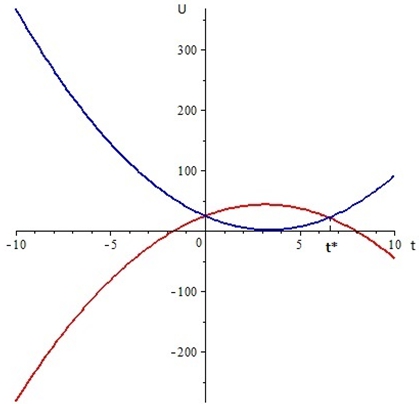
Рис. 1 – График динамики прибыли конкурирующих фирм по времени
В данной модели равновесие Нэша будет сильным, в связи с тем, что отклонение от него грозит минимизацией прибыли, а значит и банкротством.
Дополнительное исследование: определение оптимальной цены продаж с помощью дуополии Бертрана
В качестве дополнения к прогнозу по времени, с помощью дуополии Бертрана найдем оптимальную цену для продажи обеими фирмами с учетом конкуренции.
Данная модель описывает поведение фирм, конкурирующих только за счет изменения уровня цен на свою продукцию. Парадокс модели Бертрана— конкуренты будут назначать цену, равную предельным издержкам, как и фирмы в условиях совершенной конкуренции.
Согласно [2], [8] аналогичным образом, как и в определении оптимального времени продаж, составим уравнение выигрышей и найдем равновесие Нэша.
Введем следующие обозначения:
c - это себестоимость товара c1, c2 - цена на товар k - коэффициент взаимозаменяемости товаров q - начальный спрос на товар.Выигрыши игроков будут определяться соотношениями:
![]()
Важно отметить, что в данной конфликтной постановке игра задана полностью. И решение данной задачи существует в единственной точке [3, c.8], в отличие от дуополии Курно, которую и требуется определить. В данном сценарии сувенирные товары, выпускаемые конкурентами идентичны, поэтому коэффициент взаимозаменяемости примем равным за 1.
Используя вышеперечисленные финансовые показатели, были построены графики издержек, а также с помощью программы Wolfram Mathematica и с применением метода интерполяции полиномом Лагранжа были получены функции выигрышей для компании 1 и 2.
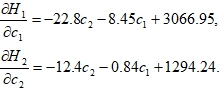
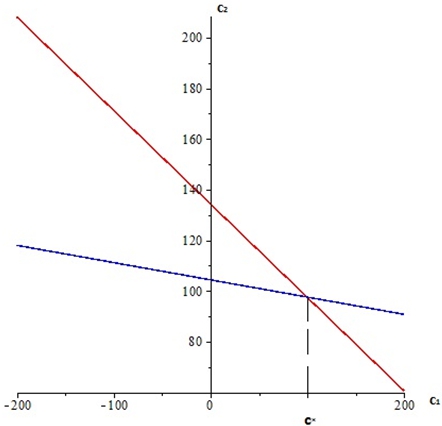
Рис.2 – Равновесие Нэша в дуополии Бертрана для двух конкурирующих фирм
Таким образом, первой фирме выгоднее будет снизить стоимость от 105 руб. 90 коп. до 99 руб. 95 коп., а второй, наоборот, повысить цену с 95 руб до 97 руб.66 коп. Данная точка является равновесием Нэша для обеих фирм, и им не выгодно отклонятся от этих конкурентных цен на свою сувенирную продукцию.
В этом случае, если конкурентная цена устанавливается равной предельным издержкам, то ни одна из компаний не получит прибыли. С другой стороны, если одна из фирм устанавливает цену, соответствующую предельным издержкам, а вторая фирма поднимает свою цену выше себестоимости единицы продукции, то прибыли просто не будет, так как все покупатели обратятся к первой фирме, устанавливающей ту же цену ниже. Равновесия не будет в сценарии с фирмами, устанавливающими различные цены.
Таким образом, равновесие в модели Бертрана существует, в случае, когда обе фирмы устанавливают именно конкурентную цену. Важно отметить, что равновесие Нэша в этой модели является слабым. Конкуренты не будут в проигрыше, если отклонятся от конкурентной цены. Эта ситуация экономически «безопасна». В данном равновесии каждая фирма может заработать не более, чем нулевая прибыль, но при условии, что конкурент установит свою цену и будет удовлетворять все потребности потребителей по этой цене.
Важно отметить, самой выигрышной стратегией в этом случае будет кооперация обоих конкурентов, тогда они смогут установить монопольную цену. На практике это может быть невозможно, поэтому применение данной модели будет зависеть от способности договориться.
Основные результаты
В соответствии со значениями издержек конкурирующих фирм 1 и 2, выпускающих одинаковую линейку сувенирных товаров, с помощью интерполяции были получены функции издержек обеих компаний, зависящие от параметра t. Была решена задача на нахождение максимума прибыли для каждой компании. В результате решения была получена точка пересечения графиков прибыли, ее координаты ![]() . Взяв положительное значение t, несложно определить ординату, координаты
. Взяв положительное значение t, несложно определить ординату, координаты ![]() – это положение, при котором стратегия обоих конкурентов «попадает» в состояние равновесия по Нэшу, то есть она является оптимальной по времени для продажи товара каждой из фирм.
– это положение, при котором стратегия обоих конкурентов «попадает» в состояние равновесия по Нэшу, то есть она является оптимальной по времени для продажи товара каждой из фирм.
На рис.1 по оси абсцисс обозначены месяцы 2020 года, точка ![]() соответствует концу июня, началу июля. Именно это время будет оптимальным для продажи продукции в условиях конкуренции и дуополии.
соответствует концу июня, началу июля. Именно это время будет оптимальным для продажи продукции в условиях конкуренции и дуополии.
Данный результат вполне объясним тем, что именно это время является туристическим сезоном, и сувенирная продукция достаточно востребована.
Значит, два крупных конкурента, производящих линейку однородной сувенирной продукции получат максимальную прибыль в этот период времени, не смотря на тот факт, что каждая из них захочет максимизировать прибыль.
Модель Бертрана позволила рассчитать конкурентную цену для продажи сувенирной продукции в обозначенный период времени. Равновесие Нэша в данной модели - это цены, которые обеспечат максимальную прибыль обеим фирмам, ![]() .
.
На примере конкуренции двух крупных производителей однородной продукции сувениров на рынке был получен достаточно простой результат, объясняющий «удобное» время продаж. Данный сценарий интересен тем, что постановка дуополии Курно позволяет найти равновесие не по цене или объему выпускаемой продукции, а по параметру времени. Без использования статистических методов прогнозирования и учитывая конфликт, именно дуополии позволяют построить достаточно точный прогноз.
Можно сделать важный вывод о том, что в данной постановке под равновесием в дуополии Курно понимается такой период времени в сочетании с объемом продаж для каждого из фирм-конкурентов, при котором ни у одной из них отсутствует мотивация изменять свои стратегии. Прибыль каждой фирмы максимальна в этой точке, при условии, что конкурент будет продавать в этот же момент времени. Иначе: в точке равновесия дуополии Курно ожидаемый конкурентами сезон продаж запланированного объема продукции любой из фирм совпадает с фактическим, являясь оптимальным. Наличие равновесия в таком сценарии модели Курно говорит о том, что олигополия, как часть и вид рынка допускает устойчивость по времени.
Математическая теория игр позволяет, используя относительно несложный математический аппарат, получить простой и ясный для понимания результат для дуополистов. Одним из важных событий для достижения равновесия является предсказуемость стратегий фирмы-конкурента. Однако именно это может усложнить практическую реализацию данной модели, так как в условиях «экономических соревнований» оценить будущие стратегии соперника может быть проблематично.
Для данного сценария с помощью модели Бертрана получены конкурентные цены, выгодные с точки зрения получения максимальной прибыли.
Важно подчеркнуть, что данные результаты были получены без статистического аппарата.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Беллман Р. Динамическое программирование. - М.: Изд-во иностр. Лит., 2009. - 400 с.
- Мазалов В.В Переговоры. Математическая теория./В.В. Мазалов, А.Э. Менчер, Ю.С. Токарева. – Спб.:Лань, 2012. – 304 с.
- Мазалов В.В. Математическая теория игр и приложения. Спб.: Лань, 2016. – 448 с.
- Петросян, Л.А. Теория игр: учеб. пособие для ун-тов / Л.А. Петросян, Н.А. Зенкевич, Е.А. Семина. – М.: Высшая школа, Книжный дом «Университет», 1998. – 304 с.
- Райзберг Б.А. Современный экономический словарь / Б.А. Райзберг, Л.Ш. Лозовский, Е.Б. Стародубцева. - 6-е изд., перераб. и доп. - М. «ИНФРА-М», 2011
- Самарский А.А. Теория разностных схем.- М.: Наука, 2009. - 616 с.
- Экономика: учебник / Под ред. А.И. Архипова, А.К. Большакова. 3-е изд., перераб. и доп. – Москва: Проспект, 2013. – 848 с.
- Экономическая теория: учебник / Под ред. А.И. Архипова, С.С. Ильина. – М.: ТК Велби, Изд-во Проспект, 2008. – 608 с.
Список литературы на английском языке / References in English
- Bellman R. Dinamicheskoe programmirovanie [Dynamic programming]. - Moscow: Izd-vo Inostr. Lit., 2009. - 400 p.
- Mazalov V.V. Peregovory. Matematicheskaja teorija [Negotiations. The mathematical theory] /V. V. Mazalov, A. E. Mencher, J. S. Tokareva. Saint Petersburg: LAN, 2012. 304 p.
- Mazalov V. V. Matematicheskaja teorija igr i prilozhenija [Mathematical theory of games and applications]. Saint Petersburg: LAN, 2016. - 448 p.
- Petrosyan, L. A. Teorija igr: ucheb. posobie dlja un-tov [Game Theory: textbook. manual for Universities] / L. A. Petrosyan, N. A. Zenkevich, E. A. Semina. - M.: Higher school, book house "University", 1998. - 304 p.
- Raizberg B. A. Sovremennyj jekonomicheskij slovar' [Modern economic dictionary] / B.A. Rajzberg, L.Sh. Lozovskij, E.B. Starodubceva. - 6th ed., reprint. and additional-M. "INFRA-M", 2011
- Samarsky A. A. Teorija raznostnyh shem [Theory of difference schemes]. - Moscow: Nauka, 2009. - 616 p.
- Jekonomika: uchebnik [Economy: textbook]. ed by A. I. Arkhipov and A. K. Bolshakov. 3rd ed., reprint. and additional – Moscow: Prospect, 2013. - 848 p.
- Jekonomicheskaja teorija: uchebnik [Economic theory: textbook] /ed by A. I. Arkhipov, S. S. Ilyin, Moscow: TC velby, Prospekt publishing House, 2008, 608 p.
