ВНУТРЕННИЕ И ПОВЕРХНОСТНЫЕ ВОЗМУЩЕНИЯ ПРИРОДНЫХ СТРАТИФИЦИРОВАННЫХ СРЕД
Булатов В.В.1 Владимиров Ю.В.2
1Профессор, Институт проблем механики им А.Ю.Ишлинского РАН; 2Кандидат физико-математических наук, Институт проблем механики им.А.Ю.Ишлинского РАН
ВНУТРЕННИЕ И ПОВЕРХНОСТНЫЕ ВОЗМУЩЕНИЯ ПРИРОДНЫХ СТРАТИФИЦИРОВАННЫХ СРЕД
Аннотация
В статье рассмотрены вопросы, связанные с дистанционным наблюдением поверхностных и внутренних гравитационных волн в природных стратифицированных средах (океане, атмосфера). Обсуждены основные теоретические предпосылки волновой теории, позволяющие строить алгоритмы обнаружения.
Ключевые слова: внутренние и поверхностные гравитационные волны, динамика океана.
Bulatov V.V.1, Vladimirov Yu.V.2
1Professor, Institute for Problems in Mechanics RAS; 2PhD, Institute for Problems in Mechanics RAS
INTERNAL AND SURFACE WAVES IN NATURAL STRATIFIED MEDIUMS
Abstract
The papere deals with issues related to the remote surveillance of surface and internal gravity waves in natural stratified media (ocean, atmosphere). Discussed the basic theoretical background of the wave theory, allowing to build detection algorithms.
Keywords: internal and surface gravity waves, ocean dynamics.
Введение
Дистанционные методы играют все более значительную роль при изучении волновой динамики океана и атмосферы [1-6]. Основным средством изучения неоднородностей, например, в толще океана должны служить низкочастотные звуковые волны, на использовании которых основана, в частности, акустическая томография. Однако существует ряд задач, которые вряд ли целесообразно решать с помощью акустических средств. Во-первых, акустические неоднородности в океане обычно весьма слабы, и необходимость их регистрации предъявляет жесткие требования к соответствующим системам излучения, приема и обработки. Во-вторых, изучение приповерхностных слоев океана акустическими методами обычно возможно лишь на небольших дистанциях, в основном с помощью зондирования направленным ультразвуком. Здесь может применяться диагностика сверху радиолокационными и оптическими средствами, в частности, даже простое фотографирование с корабля, самолета, искусственного спутника – дает массу информации о морской поверхности (рис.1). Однако такая диагностика наиболее эффективны именно для изучения поверхности – поверхностных волн, температурных свойств тонкого приповерхностного слоя, сильных внутренних волн, синоптических вихрей, оказывающих достаточно выраженное влияние на спектр поверхностных волн. Однако даже в этом случае получить достоверные количественные данные здесь не так просто.
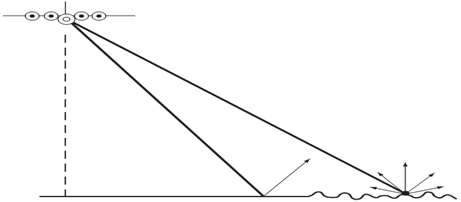
Рис.1 - Схема дистанционного зондирования океанической поверхности
Поэтому необходимо рассматривать и другие возможности изучения океанических неоднородностей и движений. Эти возможности связаны с искусственным возбуждением в морских условиях поверхностных и внутренних волн с целью изучения либо их самих, либо, с их помощью, других гидрофизических характеристик океана, например, параметров течений. Использование внутренних и поверхностных гравитационных волн для целей локации выглядит непривычно и вызывает некоторые очевидные возражения: скорость их распространения мала, и возбуждать их, на первый взгляд, трудно. Однако, во-первых, время изменчивости изучаемых процессов часто очень велико, а, во-вторых, требуемая мощность возбуждаемых волн оказывается не такой уж большой. С другой стороны, использование «медленных» волн имеет и явные преимущества. Так, при использовании поверхностных волн при изучении океанических течений сразу выявляются, по крайней мере, три достоинства. В отличие от акустических волн, на скорость поверхностных волн не оказывают заметного влияния изменения температуры морской среды, играющие основную роль в акустической томографии. Кроме того, чувствительность метода очень велика. Так, типичные скорости главных течений и синоптических вихрей ![]() имеют порядок 0.1-1 м/с. Очевидно, что относительные изменения времен задержек (волновых чисел зондирующих волн) имеют порядок
имеют порядок 0.1-1 м/с. Очевидно, что относительные изменения времен задержек (волновых чисел зондирующих волн) имеют порядок ![]() , где
, где ![]() – фазовая скорость волны. Для звука эта величина порядка
– фазовая скорость волны. Для звука эта величина порядка ![]() , тогда как для поверхностных волн с периодом в несколько секунд она составляет единицы и десятки процентов. Также локальные скорости течений определяются локальными свойствами зондирующих поверхностных волн, и ее измерения не требуют решения сложных томографических задач. Внутренние гравитационные волны еще более чувствительны к изменениям условий их распространения [1-3, 5].
, тогда как для поверхностных волн с периодом в несколько секунд она составляет единицы и десятки процентов. Также локальные скорости течений определяются локальными свойствами зондирующих поверхностных волн, и ее измерения не требуют решения сложных томографических задач. Внутренние гравитационные волны еще более чувствительны к изменениям условий их распространения [1-3, 5].
Основные подходы к процедурам дистанционных измерений волн
Сущность измерения приповерхностных течений посредством возбуждения поверхностных волн заключается в следующем. Пусть в некоторой точке морской акватории установлены два источника поверхностных волн (волнопродукторы), возбуждающие гармонические во времени поверхностные волны . Эти волны попадают в исследуемый участок акватории, в котором существуют приповерхностные течения с горизонтальной скоростью ![]() , где
, где ![]() – горизонтальные координаты. Предполагается, что длина возбуждаемых поверхностных волн λ мала по сравнению с масштабом течения в горизонтальной плоскости и течение в вертикальной плоскости можно считать однородным до глубины порядка
– горизонтальные координаты. Предполагается, что длина возбуждаемых поверхностных волн λ мала по сравнению с масштабом течения в горизонтальной плоскости и течение в вертикальной плоскости можно считать однородным до глубины порядка ![]() . Впрочем, последнее предположение менее существенно, поскольку действие неоднородного по глубине течения эквивалентно действию однородного течения с эффективной скоростью
. Впрочем, последнее предположение менее существенно, поскольку действие неоднородного по глубине течения эквивалентно действию однородного течения с эффективной скоростью ![]() , k - волновое число, z - глубина. Поэтому для целей обнаружения можно рассматривать сравнительно короткую поверхностную волну на плавно неоднородном горизонтальном течении. Для такой волны локально справедливо обычное дисперсионное соотношение с учетом влияния потока:
, k - волновое число, z - глубина. Поэтому для целей обнаружения можно рассматривать сравнительно короткую поверхностную волну на плавно неоднородном горизонтальном течении. Для такой волны локально справедливо обычное дисперсионное соотношение с учетом влияния потока: ![]() . Если частота волны ω известна (она совпадает с часто колебаний волно-продуктора, если только течение не испытывает каких-либо быстрых и сильных изменений во время измерений), то измеряя волновой вектор k, определяем проекцию Uk на направление вектора k
. Если частота волны ω известна (она совпадает с часто колебаний волно-продуктора, если только течение не испытывает каких-либо быстрых и сильных изменений во время измерений), то измеряя волновой вектор k, определяем проекцию Uk на направление вектора k ![]() . Если в месте измерения существуют две волны с разными k, то таким образом определяются две проекции вектор скорости
. Если в месте измерения существуют две волны с разными k, то таким образом определяются две проекции вектор скорости ![]() , и этот вектор будут известен полностью. Выбирая оси координат x,y зная углы волновых векторов β относительно этих осей и проекции
, и этот вектор будут известен полностью. Выбирая оси координат x,y зная углы волновых векторов β относительно этих осей и проекции ![]() скорости на направления ki с помощью геометрических соображений получим модуль вектора
скорости на направления ki с помощью геометрических соображений получим модуль вектора ![]() и угол между ним и осью z
и угол между ним и осью z
![]()
где i=1,2 соответствуют двум возбуждаемым волнам. Таким образом, задача сводится к измерению волнового вектора волны в той же акватории, точнее в области, большей по сравнению с длиной волны, но малой по сравнению с масштабом изменения ![]() , где нужно определить течения. Поэтому достаточно иметь локальную информацию о волнах, а снимок или радиолокационное изображение большой акватории, сделанный с самолета или искусственного спутника, позволяет измерить течение во всех точках этой акватории [4,6,11,12].
, где нужно определить течения. Поэтому достаточно иметь локальную информацию о волнах, а снимок или радиолокационное изображение большой акватории, сделанный с самолета или искусственного спутника, позволяет измерить течение во всех точках этой акватории [4,6,11,12].
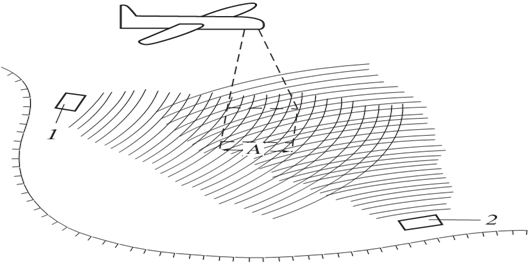
Рис.2 - Схема метода изучения приповерхностных течений (выхода внутренних волн на поверхность) с помощь искусственно возбуждаемых поверхностных волн: 1,2 – волнопродукторы, А – размер «окна наблюдения»
В настоящее время общепризнанно, что внутренние волны являются одним из важнейших факторов, определяющих уровень турбулентности и тонкой структуры океана, и влияют на состояние морской поверхности, регистрируемое с помощью средств космической океанографии. В то же время, степень изученности процессов взаимодействия внутренних волн с другими гидрофизическими полями все еще очень мала, несмотря на растущий интерес к этим исследованиям. Основная причина заключается в трудности эксперимента, связанного с тщательным количественным измерением различных волновых возмущений и установлением корреляций между ними. Дело осложняется тем, что условия эксперимента обычно зависят от ряда неконтролируемых факторов, в том числе от параметров внутренних волн, приходящих в точку наблюдений. В настоящее время известны единичные эксперименты по прямому наблюдению взаимодействия внутренних волн с турбулентностью и поверхностными волнами в натурных условиях. Но даже в этих случаях трудно обеспечить повторяемость результатов из-за изменчивости полей внутренних волн в реальных океанических условиях [7-12].
Поэтому перспективным представляется искусственное возбуждение внутренних волн в морских условиях с помощью, например, специальных волнопродукторов – генераторов, источников волновых возмущений. Это может позволить получить калиброванные волны с достаточно хорошо контролируемыми и стабильными параметрами. В свою очередь стабильность такого «сигнала» создает возможность его возбуждения и обнаружения даже на фоне сильной помехи с помощью стандартных метода обработки, обычных для радиофизики и акустики. Некоторые методы обработки натурных океанологических данных, позволяющие выделить «сигнал» (пакеты распространяющихся внутренних волн) на фоне больших помех изложены, в частности, в [1-3]. Очевидно, вряд ли целесообразно пытаться «засветить» искусственными внутренними волнами всю толщу океана – целесообразно использовать верхний (сезонный) термоклин, как некоторое канализирующее устройство. Следовательно, речь может идти о достаточно высокочастотных внутренних волнах, которые могут быть локализованы в сезонном термоклине, где уровень фона изучен относительно слабо. Поэтому, вначале необходимо рассматривать волнопродуктор, который установлен в области морского шельфа, где «внутренняя погода» (шумы, не связанные с внутренними волнами) обычно спокойнее. Этот волнопродуктор должен «засвечивать» сравнительно небольшую акваторию, порядка 1-10 км, в которой внутренняя волна может надежно выделяться на фоне помех. Еще лучше, если на небольших расстояниях (порядка сотен метров) волна могла бы оказывать заметное воздействие на уровень турбулентности в районе термоклина. Это создало бы возможность контролировать не только распространение внутренних волн, но и их вторичные проявления.
Чтобы получить предварительно качественное представление о возможности выполнения этих условий предположим, что источник волн (волнопродуктор) находится под или над максимумом термоклина, который моделируется скачком плотности. В качестве источника волновых возмущений можно рассмотреть следующие модели: горизонтально лежащий цилиндр, совершающий вертикальные колебания и вертикально расположенная пластина, колеблющаяся около горизонтальной оси. Действие этих источников волновых возмущений может быть приближенно представлено системой источников и стоков. Так, цилиндр, в первом приближении представим системой диполей, а тонкая пластина системой монополей, и тогда для расчета генерируемых этими источниками дальних полей внутренних волн можно использовать основные результаты линейной теории [1-3].
Теоретические предпосылки дистанционного зондирования
При дистанционном зондировании можно получить сведения об изменениях спектра морской поверхности по результатам обратного (резонансного) рассеяния радиоволн [4,6,9,12]. Эти изменения (контрасты), как правило, вызваны поверхностными течениями, связанными в том числе, с выходом внутренних гравитационных волн на поверхность океана. Упрощенно модель изменения морского спектра под влиянием поверхностных течений можно описать следующим образом. Обозначим через ![]() энергетический спектр морской поверхности,
энергетический спектр морской поверхности, ![]() - координаты на этой поверхности, k - волновой вектор, t - время. Согласно известной модели взаимодействия поверхностного течения, которое определяется полем скоростей
- координаты на этой поверхности, k - волновой вектор, t - время. Согласно известной модели взаимодействия поверхностного течения, которое определяется полем скоростей ![]() , водится величина
, водится величина ![]() , где
, где ![]() - дисперсионное соотношение, например, для длинных поверхностных волн, k - модель волнового вектора. Эта величина называется плотностью волнового действия. Тогда вдоль траектории системы
- дисперсионное соотношение, например, для длинных поверхностных волн, k - модель волнового вектора. Эта величина называется плотностью волнового действия. Тогда вдоль траектории системы
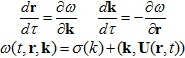
где выполняется равенство ![]() . Введем групповую скорость
. Введем групповую скорость ![]() , и тогда это условие имеет вид:
, и тогда это условие имеет вид: ![]() . Данное выражение можно рассматривать, как уравнение для определения величины А. В реальных океанических условиях спектр поверхностного волнения может быть представлен в виде, не зависящем от времени. Тогда уравнение имеет явные решения, которые позволяют по данным обратного рассеяния радиоволн получать определенную информацию о зонах поверхности моря, занятого течениями и иными поверхностными проявлениями внутренних волн [6,12].
. Данное выражение можно рассматривать, как уравнение для определения величины А. В реальных океанических условиях спектр поверхностного волнения может быть представлен в виде, не зависящем от времени. Тогда уравнение имеет явные решения, которые позволяют по данным обратного рассеяния радиоволн получать определенную информацию о зонах поверхности моря, занятого течениями и иными поверхностными проявлениями внутренних волн [6,12].
Несмотря на то, что еще никому не удалось измерить полный спектр внутренних гравитационных волн в океане, имеющиеся оценки различных сечений и проекций спектра позволяют получить представление об основных чертах этого спектра. Использовав известные факты и теоретические представления, а также сделав ряд смелых, была сделан попытка увязать данные по одномерным спектрам температуры и полей течений в различных районах Мирового океана в рамках известной единой модели спектра внутренних гравитационных волн Гарретта и Манка. Эта модель базируется на следующих основных предположениях [4,7]:
1)наблюдаемые колебания гидрофизических характеристик волновых полей и течений в пространстве и во времени определяются исключительно внутренними гравитационными волнами;
2) наблюдаемые волновые поля образуются суперпозицией свободных линейных волн со случайными фазами и может быть описана в рамках ВКБ приближения метода геометрической оптики (рис.3-5);
3)энергия волн распределена непрерывно в пространстве частот и волновых чисел, а не сосредоточена вдоль отдельных поверхностей, соответствующим отдельным волновым модам – модальный континуум вместо дискретных мод;
4)волновое поле обладает вертикальной симметрией, то есть потоки энергии вверх и вниз одинаковы;
5)волновое поле горизонтально изотропно;
6)данные измерений волновых полей, собраны в различных местах и в разное время описывают приблизительно одно и то же универсальное волновое поле
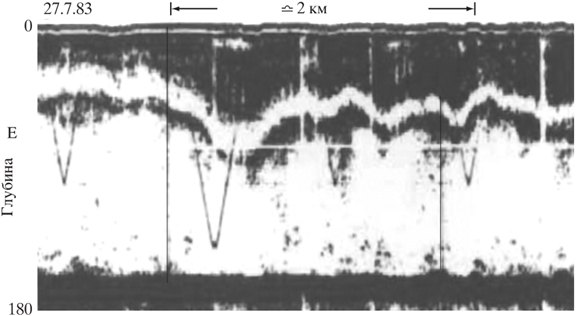
Рис.3 - Внутренняя гравитационная волна, двигающаяся влево в Кельтском море (1983 г.), хорошо описываемая линейной теорией (волна Эйри)
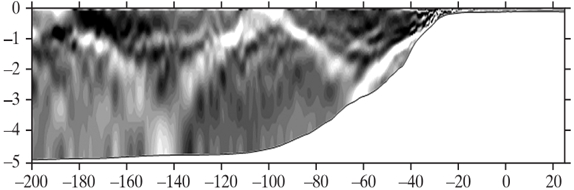
Рис.4 - Внутренние приливные гравитационные волны на шельфе Бискайского залива – наблюдаемая ярко выраженная лучевая модовая структура волновых пакетов (ВКБ приближение)
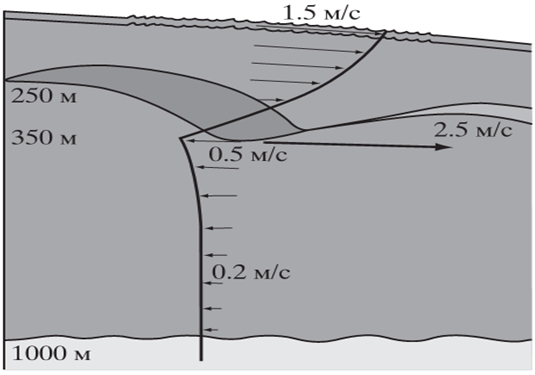
Рис.5 - Внутренние гравитационные волны в море Сулу: шкалированный срез скоростей
Все эти предположения позволили создать простую модель полного спектра внутренних волн в океане, но некоторые из них нельзя принять безоговорочно. Первое предположение кажется наиболее оправданным для временных записей изменчивости гидрофизических полей в океане, поскольку диапазон свободных внутренних волн имеет четкие границы – частоту плавучести Брента-Вяйсяля и инерционную частоту [4,7-12]. В этих границах, как показывают данные большинства океанологических измерений, колебания, связанные с внутренними волнами, действительно доминируют. Сложнее обстоит дело с изменчивостью гидрофизических полей вдоль горизонтальных и особенно вертикальных направлений. Внутренние волны имеют четкое ограничение пространственных масштабов лишь сверху, со стороны длинных волн. Максимальная длина волны полностью определяется дисперсионной зависимостью низшей волновой моды. Как показывают многочисленные данные натурных океанических и атмосферных наблюдений, внутренние гравитационные волны не всегда могут доминировать над пространственными колебаниями иного происхождения, например фронтами и синоптическими вихрями в горизонтальном направлении (рис.6-8) [4, 7-12].

Рис.6 - Внутренние гравитационные волны в проливе Карских ворот Баренцева моря (съемки со спутника «Алмаз», 1991 г.)

Рис.7 - Волновой пакет вдоль края континентального шельфа у архипелага Вестеролен в Норвежском море. В каждой группе 10-15 волн (фото спутника ERS-2 16 августа 2000г.)

Рис.8 - Атмосферные внутренние гравитационные волны за Южными Сандвичевыми островами в Южной Атлантике (58° ю.ш., 36° з.д.) на снимке спутника Aqua (02.11.2004, 20h15m UTC). Площадь наибольшего острова 110 кв.км, максимальная высота над уровнем моря 1372 м.
Предположение о линейности волн и допустимости ВКБ приближений позволяет установить связи между различными компонентами волновых движений на различных горизонтах и между пространственными и временными частотами волн. Имеющиеся наблюдения за параметрами внутренних волн не обнаруживают существенных отклонений от дисперсионных соотношений, вытекающих из линейной теории (рис.3-5). Что касается ВКБ приближений (приближений геометрической оптики), то они оправданы далеко не всегда, в частности они неприменимы при резких изменениях частоты плавучести Брента-Вяйсяля, рельефа дна, вблизи точек поворота лучей. Предположение о модальном континууме представляется даже более реалистичным, чем картина дискретных волновых мод, так как реальный океан слишком изменчивая среда, для того чтобы отдельные моды могли сформироваться у колебаний всех масштабов. Достаточно сказать, что скорость переменных течений сопоставима со скоростью внутренних волн, и размытие дискретного спектра может быть значительным.
Также может быть оправданным в значительной мере и допущение о вертикальной симметрии поля, тогда как горизонтальная изотропность внутренних волн – свойство, далеко не обязательное. Но поскольку это допущение сильно упрощает модель (горизонтальная изотропия может быть присуща волновым полям вдали от источников возмущений), его можно использовать. Самым оторванным от реальности представляется предположение об универсальности измеряемых в различных районах Мирового океана гидрофизических полей, так как оно полностью пренебрегает изменчивостью и разнообразием гидрологических параметров океана. Однако, несмотря на идеализирующие предположения, модель Гарретта-Манка неплохо описывает волновые колебания в океане. Эта модель выдержала проверки предпринятые многочисленными исследователями в разных районах Мирового океана[4,7].
Заключение
Результаты теоретического изучения генерации и распространения внутренних гравитационных волн, могут быть использованы для описания, в том числе, волнового шлейфа в океане за движущимся тропическим циклоном (ураганом), подветренных волн в стратифицированной атмосфере при обтекании орографических препятствий (изолированных гор, островов в океане) и многочисленных других задач волновой динамики природных стратифицированных сред. В частности, в формировании волновых картин в атмосфере Земли участвуют инерционно-гравитационные волны, обусловленные плотностной стратификацией этой природной среды. Представленная на рис.8 картина фазовых линий полей внутренних гравитационных волн в атмосфере качественно подобна известной волновой картине корабельных волн от движущегося источника возмущений . Здесь так же присутствуют боковые и поперечные волны, отвечающие различным ветвям фазовых кривых. Основное отличие, как известно, состоит в том, что для корабельных волн угол полураствора волнового клина θ ≈ 19.5° не зависит от скорости перемещения источника волновых возмущений. В то же время для подветренных волн в стратифицированной вращающейся атмосфере Земли эта зависимость очень сильная. Интересно отметить, что картины подветренных волн обнаруживаются даже на спутниковых фотографиях атмосферы Марса. Таким образом, полученные аналитические представления фазовых поверхностей образуют волновую картину полей внутренних гравитационных волн от движущегося локализованного источника. Поэтому на основе этих представлений можно изучать структуры волнового шлейфа в океане за движущимся тропическим циклоном (ураганом), системы подветренных волн в атмосфере Земли и другие задачи эволюции волн в природных стратифицированных сред, имеющие, в том числе, прикладное значение.
Литература
- Bulatov V.V., Vladimirov Yu.V. Internal gravity waves: theory and applications. Moscow: Nauka Publishers, 2007, 304 p.
- Булатов В.В., Владимиров Ю.В. Динамика негармонических волнох пакетов в стратифицированных средах. М.: Наука, 2010, 470 с.
- Bulatov V.V., Vladimirov Yu.V. Wave dynamics of stratified mediums. Moscow: Nauka Publishers, 2012, 584 p.
- Коняев К.В., Сабинин К.Д. Волны внутри океана. СПб.: Гидрометеоиздат, 1992, 272 с.
- Sutherland B.R. Internal gravity waves. Cambridge: Cambridge University Press, 2010, 394 p.
- Методы, процедуры и средства аэрокосмической радиотомографии приповерхностных областей Земли / Под ред. С.В.Нестерова, А.С.Шамаева, С.И.Шамаева. М.: Научный мир, 1996. 272 с.
- Garrett C, Kunze E. Internal tide generation in the deep ocean //Review Fluid Mechanics. - 2007. - Vol. 39. - P. 57-87.
- Song Z.J., Gou B.Y., Lua L., Shi Z.M., Xiao Y., Qu Y. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses //Applied Ocean Research. - 2011. - Vol.33. - P.120-129.
- Hsu M.K., Liu A.K., Liu C. A study of internal waves in the China Seas and Yellow Sea using SAR // Continental Shelf Research. - 2000. - Vol. 20. - P. 389-410.
- Grue J., Sveen J.K. A scaling law of internal run-up duration // Ocean Dynamics. - 2010. - Vol. 60. - P.993-1006.
- Grue J., Jensen A. Orbital velocity and breaking in steep random gravity waves // J Geophysical Research. - 2012. - Vol. 117. - P. C07-C013.
- Doong D.J., Lee B.C., Kao C.C. Wave measurement using GPS velocity signal //Sensors. - 2011. - Vol. 11. - P.1043-1058.
References
- Bulatov V.V., Vladimirov Yu.V. Internal gravity waves: theory and applications. Moscow: Nauka Publishers, 2007, 304 p.
- Bulatov V.V., Vladimirov Ju.V. Dinamika negarmonicheskih volnoh paketov v stratificirovannyh sredah. M.: Nauka, 2010, 470 s.
- Bulatov V.V., Vladimirov Yu.V. Wave dynamics of stratified mediums. Moscow: Nauka Publishers, 2012, 584 p.
- Konjaev K.V., Sabinin K.D. Volny vnutri okeana. SPb.: Gidrometeoizdat, 1992, 272 s.
- Sutherland B.R. Internal gravity waves. Cambridge: Cambridge University Press, 2010, 394 p.
- Metody, procedury i sredstva ajerokosmicheskoj radiotomografii pripoverhnostnyh oblastej Zemli / Pod red. S.V.Nesterova, A.S.Shamaeva, S.I.Shamaeva. M.: Nauchnyj mir, 1996. 272 s.
- Garrett C, Kunze E. Internal tide generation in the deep ocean //Review Fluid Mechanics. - 2007. - Vol. 39. - P. 57-87.
- Song Z.J., Gou B.Y., Lua L., Shi Z.M., Xiao Y., Qu Y. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses //Applied Ocean Research. - 2011. - Vol.33. - P.120-129.
- Hsu M.K., Liu A.K., Liu C. A study of internal waves in the China Seas and Yellow Sea using SAR // Continental Shelf Research. - 2000. - Vol. 20. - P. 389-410.
- Grue J., Sveen J.K. A scaling law of internal run-up duration // Ocean Dynamics. - 2010. - Vol. 60. - P.993-1006.
- Grue J., Jensen A. Orbital velocity and breaking in steep random gravity waves // J Geophysical Research. - 2012. - Vol. 117. - P. C07-C013.
- Doong D.J., Lee B.C., Kao C.C. Wave measurement using GPS velocity signal //Sensors. - 2011. - Vol. 11. - P.1043-1058.
