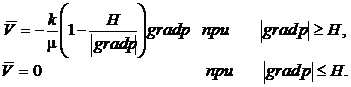ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ КРИТИЧЕСКИХ ГРАДИЕНТОВ ДАВЛЕНИЯ И СКОРОСТИ ФИЛЬТРАЦИИ НЕНЬЮТОНОВСКОЙ ЖИДКОСТИ

Шевченко О.Н.

ORCID: 0000-0003-1805-5969, аспирант, Самарский государственный технический университет

ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ КРИТИЧЕСКИХ ГРАДИЕНТОВ ДАВЛЕНИЯ И СКОРОСТИ ФИЛЬТРАЦИИ НЕНЬЮТОНОВСКОЙ ЖИДКОСТИ

Аннотация

Закон Дарси выполняется в определенном диапазоне скоростей фильтрации. Существуют некоторые предельные градиенты давления, при которых меняется режим фильтрационного течения. Для определения нижней границы линейной фильтрации был рассмотрен общий случай фильтрации нелинейно-вязко пластичной жидкости. Произведен расчет для определения нижней границы применимости закона Дарси для месторождений, расположенных в пластах каменноугольного возраста.

 Ключевые слова: предельный градиент давления, критическая скорость фильтрации.

Shevchenko O. N.

ORCID: 0000-0003-1805-5969, Postgraduate student, Samara State Technical University

THE DETERMINATION OF THE VALUES OF CRITICAL PRESSURE GRADIENTS AND VELOCITY FILTERING OF NON-NEWTONIAN FLUID

Abstract

Darcy's law is in a certain range of filtration velocities. There are some marginal pressure gradients, in which change the mode of a filtration flow. A general case of nonlinear filtering-visco-plastic fluid was examined to determine the lower limit of linear filtering.

Keywords: maximum pressure gradient, the critical speed of filtration.

Известно, что закон Дарси выполняется при определенных условиях. Существует нижняя граница применимости закона Дарси, которая зависит от физико-химических особенностей взаимодействия жидкости с твердым скелетом, а так же от неньютоновских реологических свойств жидкости[1,2,4].

Классическим примером закона фильтрации для неньютоновской жидкости является закон фильтрации с предельным (начальным) градиен­том [3]. Этот закон записывается для вязкопластичной жидкости Бингама-Шведова в виде [5,7]

                                      (1)

Как следует из соотношений (1), фильтрационное течение воз­можно лишь при градиентах давления, превышающих некоторое значе­ние Н, которое называется предельным градиентом. При меньших значениях градиента давления фильтрационное течение отсутствует. Величина начального градиента зависит от предельного напряжения сдвига жидкости τ₀ и эффективного диаметра капилляра d_эф.

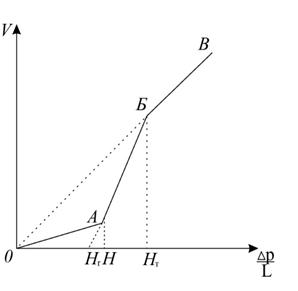
Данный закон фильтрации более общего вида, чем соотношение (1) был рассмотрен в работе [5]. Графическое представление данного закона представлено на (рис.1).На данном графике выделяется три участка: ОА - область, где жидкость фильтруется с малой скоростью и наибольшей вязкостью из-за практически неразрушенной структуры, наблюдается явление ползучести; АБ - область, здесь скорость фильтрации резко увеличивается; БВ - область, где жидкость фильтруется с полностью разрушенной структурой и наименьшей вязкостью. Продолжение участка проходит через начало координат, что соответствует о ньютоновском характере течения.  На данном графике выделяются два критических градиента давления:  - градиент давления, определяющий границу прочности практически не разрушенной структуры;  - градиент давления предельного разрушения структуры[12].

Рис. 1 - Зависимость скорости фильтрации от градиента давления для нелинейной вязкопластичной жидкости

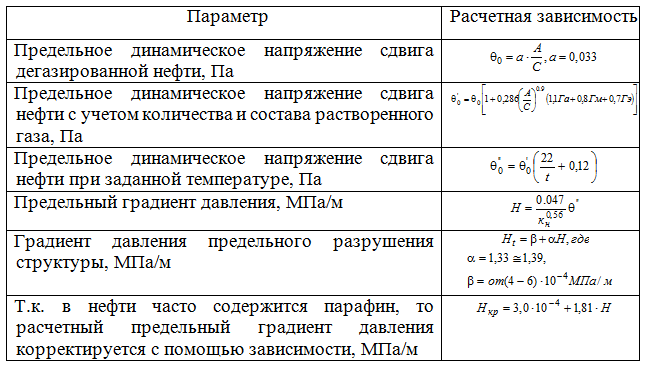
Анализируя данную зависимость можно сделать следующий вывод: существует некоторое значение Н - предельный градиента давления, при котором происходит изменение законов фильтрации жидкости. Этот предельный градиент зависит от свойств фильтрующейся жидкости. Известно, что неньютоновское поведение нефти в основном связано с повышенным содержанием в ней высокомолекулярных компонентов - асфальтенов, смол и парафина. Соответственно, для расчета критических градиентов давления нам необходимо будет знать: А, С - массовое содержание в нефти асфальтенов и смол,  % мас.; Г_а, Г_м, Г_э - содержание в нефти соответственно растворенного азота, метана и этана м³/м³; t - температуру нефти в пласте при которой происходит фильтрация, °С, kн - нефтепроницаемость коллектора, мкм². Для расчета критических градиентов давления, воспользуемся эмпирическими зависимостями представленными для нефтей карбона месторождений Татарии, так как в основном большинство залежей располагается именно в пластах каменноугольного возраста [9,7,10,11].

Таблица 1 - Эмпирические зависимости для нефтей карбона месторождений Татарии

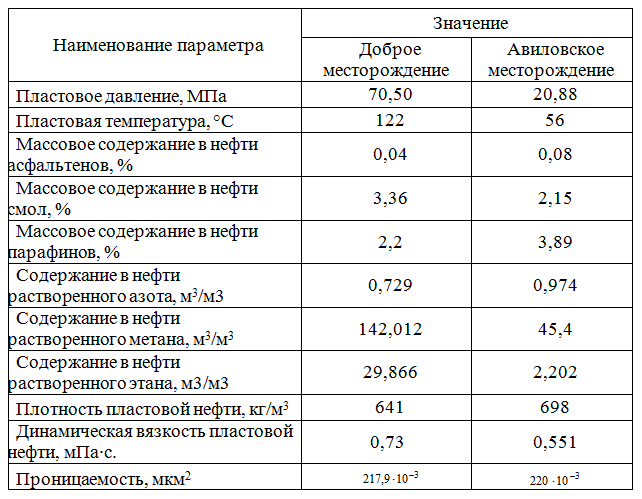
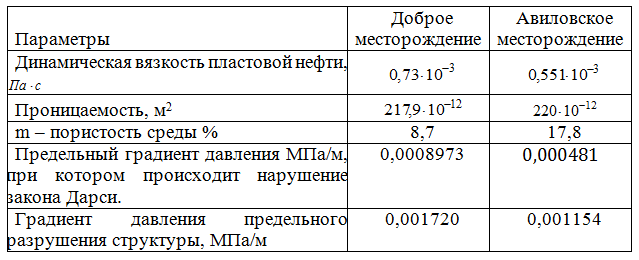
Произведем расчет особенностей фильтрации для двух нефтей. Залежь Доброго месторождения Волгоградской области расположена в пределах тиманского возраста, а так же для залежи Авиловского месторождения.

Таблица 2- Параметры месторождений

 

Результаты расчетов сведем в таблицу 3.

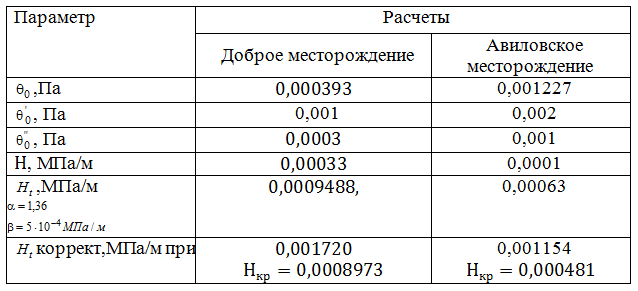
Таблица 3 - Результаты расчетов

Соответственно нам известен предельный градиент давления и градиент предельного разрушения структуры. Для залежей тиманского горизонта Доброго месторождения и для Авиловского месторождения, сведем все основные данные в таблицу 4.

Таблица 4 – Основные данные для расчета

Таблица 5 - Значение скоростей фильтрации для нижней границы применимости закона Дарси

Вычислим значения скоростей фильтрации по уравнению Бингама-Шведова для нижней границы применимости закона фильтрации Дарси, построим графическую зависимость скорости фильтрации от градиента давления для Доброго и Авиловского месторождений.

Рис. 2 - Графическая зависимость скорости фильтрации от градиента давления для  Доброго месторождения.

Рис. 3 - Графическая зависимость скорости фильтрации от градиента давления для  и Авиловского месторождения.

В результате произведенных расчетов можно описать методику определения нижней границы применимости закона фильтрации Дарси:

1. Определим расчетным методом: предельное давление насыщения дегазированной нефти, Па; предельное давление насыщения нефти с учетом количества и состава растворенного газа, Па; предельное давление насыщения нефти при заданной температуре, Па; предельный градиент давления, МПа/м; градиент давления предельного разрушения структуры, МПа/м.
2. Вычислим значения скоростей фильтрации по уравнению Бингама-Шведова, для нижней границы применимости закона фильтрации Дарси.
3. Для наглядного представления построим зависимость скорости фильтрации от градиента давления.

Заключение

Определение нижней границы применимости закона Дарси актуально для средне и высоковязких нефтей, для нефтей как Доброго, так и Авиловского месторождений определение данной границы не актуально, так как получившийся интервал значений весьма мал.

Нефти Авиловского и Доброго месторождений являются линейной-вязкопластичной жидкостью, что наглядно продемонстрировано на рисунках  2 и 3.

Литература

1. Абдулвагабов А.И. О режимах движения жидкостей и газов в пористой среде // Известия   вузов. – 1961. – № 2. – C. 8-13.
2. Басниев К.С., Кочина И.Н., Максимов В.М.. Подземная гидромеханика  - М.: Недра,1993. − 416 с.
3. Белолипецкий В.М., Бекежанова В.Б.. Некоторые вопросы теории фильтрации и гидродинамической устойчивости: Учебное пособие по практическим занятиям  - Красноярск, 2007. -  55 с
4. Герасимов Д.С. Основные определения и понятия фильтрации жидкостей и газов среды и границы применяемости закона Дарси: методическое пособие -Тюмень : ТюмГНГУ, 2013. – 41с
5. Девликамов В.В., Хабибуллин З.А., Кабиров М.М. Аномальные нефти -Москва: Недра, 1975. — 168 с
6. Желтов Ю.П. Разработка нефтяных месторождений.-М:Недра, 1986 г. - 330 с.
7. Каневская Р.Д. Математическое моделирование гидродинамических процессов разработки месторождений углеводородов.- М, 2002 г - 140 с.
8. Коллинз Р. Течение жидкостей через пористые материалы.- Москва, 1964 г- 345 л.
9. Миллионщиков М. Д., Христианович С. А., Гальперин В. Г., Симонов Л. А .Прикладная газовая динамика: В 2-х частях. Часть 1. - М., 1948. — 146 с
10. Ольховская В. А. Подземная гидромеханика. Фильтрация неньютоновской нефти. - Москва: ОАО "ВНИИОЭНГ", 2011. - 221 с.
11. Павловский Н.Н. Курс гидравлики. Часть 1.- Кобуч 1933г. 180 с

References

1. Abdulvagabov A.I. O rezhimah dvizhenija zhidkostej i gazov v poristoj srede // Izvestija vuzov. – 1961. – № 2. – C. 8-13.
2. Basniev K.S., Kochina I.N., Maksimov V.M.. Podzemnaja gidromehanika - M.: Nedra,1993. − 416 s.
3. Belolipeckij V.M., Bekezhanova V.B.. Nekotorye voprosy teorii fil'tracii i gidrodinamicheskoj ustojchivosti: Uchebnoe posobie po prakticheskim zanjatijam - Krasnojarsk, 2007. -  55 s
4. Gerasimov D.S. Osnovnye opredelenija i ponjatija fil'tracii zhidkostej i gazov sredy i granicy primenjaemosti zakona Darsi: metodicheskoe posobie -Tjumen' : TjumGNGU, 2013. – 41s
5. Devlikamov V.V., Habibullin Z.A., Kabirov M.M. Anomal'nye nefti -Moskva: Nedra, 1975. — 168 s
6. Zheltov Ju.P. Razrabotka neftjanyh mestorozhdenij.-M:Nedra, 1986 g. - 330 s.
7. Kanevskaja R.D. Matematicheskoe modelirovanie gidrodinamicheskih processov razrabotki mestorozhdenij uglevodorodov.- M, 2002 g - 140 s.
8. Kollinz R. Techenie zhidkostej cherez poristye materialy.- Moskva, 1964 g- 345 l.
9. Millionshhikov M. D., Hristianovich S. A., Gal'perin V. G., Simonov L. A .Prikladnaja gazovaja dinamika: V 2-h chastjah. Chast' 1. - M., 1948. — 146 s
10. Ol'hovskaja V. A. Podzemnaja gidromehanika. Fil'tracija nen'jutonovskoj nefti. - Moskva: OAO "VNIIOJeNG", 2011. - 221 s.
11. Pavlovskij N.N. Kurs gidravliki. Chast' 1.- Kobuch 1933g. 180 s