ПРИМЕНЕНИЕ МЕТОДОВ ОПТИМИЗАЦИИ В АРХИТЕКТУРНОМ ДИЗАЙНЕ
Чихоцка Ю.М.1, Мусихина Е. А.2
1Аспирантка Вроцлавского технического университета, Польша, в рамках программы «Эразмус Мундус. Действие 2» judyta.cichocka@gmail.com; +79149360803;
2к.т.н., проф. каф. Архитектурного проектирования НИ ИрГТУ, 664033 Иркутск, а/я 28, т. +79149057099, elena.science@ya.ru
ПРИМЕНЕНИЕ МЕТОДОВ ОПТИМИЗАЦИИ В АРХИТЕКТУРНОМ ДИЗАЙНЕ
Аннотация
Статья посвящена актуальной проблеме - исследованию применения методов оптимизации в процессе проектирования художественного оформления архитектурных объектов. Приведен исторический обзор становления теории оптимизации как науки от истоков до современных методов на основании авторских схем. На основе синтеза структуры и материальной оптимизации показывается полезность использования методов оптимизации в художественном оформлении архитектурных проектов.
Ключевые слова: оптимальное управление, методы прикладной оптимизации, классификация проблем оптимизации, параметрический дизайн.
Cichocka J.M. 1, Musikhina E.A. 2
1Master of Architecture, post graduate student Wroclaw Technical University, Poland. Supported by the Erasmus Mundus Action 2 Programme of the European Union; judyta.cichocka@gmail.com; +79149360803
2Candidate of Technical Sciences, Professor of Architecture and Design, Irkutsk State Technical University, 83 Lermontova str., Irkutsk, 664074, Russia; elena.science@ya.ru; +79149057099
METHODS OF OPTIMIZATION IN ARCHITECTURE
Abstract
Clause is devoted to an actual problem - to research of application of methods of optimization during designing decorating architectural objects. The historical review of becoming of the theory of optimization as sciences from sources up to modern methods on the basis of author's schemes is resulted. On the basis of synthesis of structure and material optimization utility of use of methods of optimization in decorating architectural projects shows.
Keywords: optimum control, methods of applied optimization, classification of problems of optimization, parametrical design.
This essay will try to investigate the genesis of optimization in architectural design as well as to point out the major design areas in architecture, which could be affected by optimization tools.
Andrej Cherkaev, who is a professor of mathematics at the University of Utah, explained the essence of the optimization problem as: "catching a black cat in a dark room in the minimal of time" [5].
This statement straightly refers to a Confucius quotation: “The hardest thing of all is to find a black cat in a dark room, especially if there is no cat is it.” The both sentences need some light to be shed on them.
Optimization is defined as the art, science and mathematics of selecting the best element according to the best element among finite or infinite available alternatives according to some specified criteria [3] . According to Boyd and Vandenberghe [2004: 1] an optimization problem, has the form;
minimize f0(x)
subject to fi(x) ≤ bi, i = 1,...,m.
Where;
- the vector x = (x1,...,xn) is the optimization variable depending on the problem,
- the function f0 : Rn → R is an objective function,
- the functions fi : Rn → R, i = 1,...,m, are (inequality) constraint functions, and the constants b1,...,bm are the limits, or bounds, for the constraints.
- A vector x⋆ is called optimal, or a solution of the problem
A default definition is formulated for finding the minimum of the objective function. In general the goal of optimization is to find some extremes: minimum or maximum value(s) for the formulated optimization problem. Referring to NEOS resources, in mathematical terms : "the goal in solving an optimization problem is to find values of the variables that minimize or maximize the objective function subject to satisfying the constraints". The NEOS Server is a project run by the University of Wisconsin - Madison that allows anyone to submit optimization problems to state-of-the-art solvers [http://www.neos-guide.org] (figure 1).
In literature some slightly different definitions of optimization problems can be found. Their exact forms depend on the specification of the optimization problems. NEOS, provides the latest taxonomy of optimization (this field of study is still being developed).
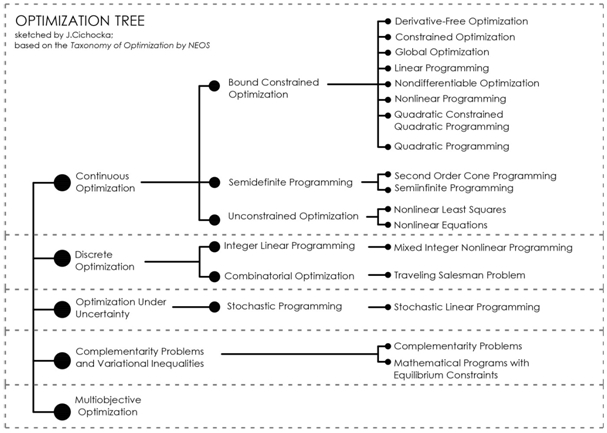
Fig. 1 – The graph below shows the taxonomy according to the date of access to the NEOS website [04.01.2014]
This diversity is a result of multitude of the types of objective functions, different data forms of variables (for instance continues or discrete) and lack or existence of constrains and their forms too. The below Boyd, Vandenberg he quotation is given to show, how to classify particular optimization problem:
"We generally consider families or classes of optimization problems, characterized by particular forms of the objective and constraint functions ." [2]
Therefore, as many prior assumptions so many optimization methods. Due to these plurality and variety, there is no silver bullet in optimization theory [5]. Moreover, the optimization problem can be feasible or infeasible.
Hence, now the difficulty of finding "black cat in a dark room" is more understandable, especially there could be no cat (no solution).
Genesis
Nevertheless, the black magic of optimization has found numerical application in many fields of study and everyday problems. The human desire for perfection gave a grain to grow an optimization theory. From the below timeline of the historical rundown of optimization (figure 2), According to Dutta this grain was given by princess Dido, but more similar stories are found in the book titled Stories about Maxima and Minima by V. M. Tikhomirov, Dutta [3].
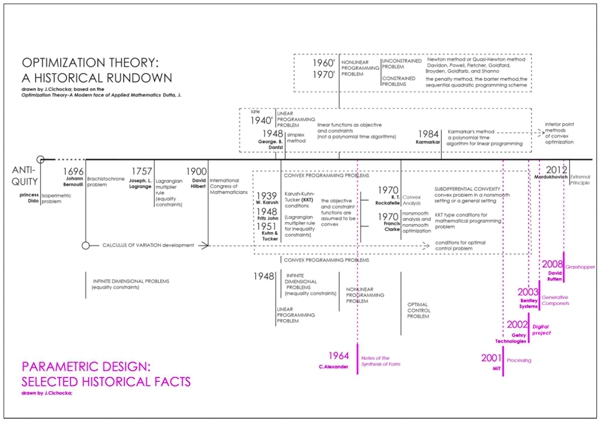
Fig. 2 – Timeline of the theory of optimization
There is no point to investigate the development of optimization theory decade by decade. The rough image of this development is presented on the timeline (drawing 1).
The basic knowledge about optimization is the Calculus of Variation. The real breakthrough discovery was made in 1948, when George Dantzig invented Linear Programming - the new class of optimization, where both objective function and constrains are linear, as they say in their book Lectures on Modern Convex Optimization:
"This breakthrough discovery included the methodological idea that a natural desire of a human being to look for the best possible decisions can be posed in the form of an optimization program (P) and thus subject to mathematical and computational treatment. " [4]
This discovery was a real impulsion for the further development of optimization [3]. The convexity is regarded as another completely new attitude to optimization. The simple feature of the convex functions, that every local minima is global, made the convexity so attractive in optimization quite theory [3].
Concerning the modern methods of optimization they could be problematic. In professional literature the term "modern methods of optimization" often appears. . It may be unattainable to point out the exact beginning of those modern methods. To show the relativeness of this term, two quotation are compared below. According to Joydeep Dutta:
"Beginning of the modern methods of optimization can be traced back to the growth of the Calculus of Variations. In fact it was Joseph. L. Lagrange who in 1757 first gave a general framework for tackling problems of the calculus of variations" [3].
When, Ben-Talt and Nemirowski claim, that classical methods, were created before 1980 and all achievements after this date are about modern optimization, as they say:
"(...) let us outline the major achievements in Optimization during the last 20 years or so, those which, we believe, allow to speak about modern optimization as opposed to the “classical” one as it existed circa 1980" [4].
Nonetheless, the undeniable is the fact, that since late 1940s, a huge effort has been put not only into developing the various classes and families of optimization problems, but also into analysis of their properties and their implementation in software applications [2].
Application in Architectural Design
The amazing amount of problems, including both practical and decision making problems can be expressed in the form of the mathematical optimization problem [2]. According to Dutta [3], linear programming is tremendously applied in "economics, military operations, business, engineering, etc". In fact, optimization is broadly used in computer science, finance, statistics, electronic design automation, engineering, scheduling, supply chain managements, aerospace engineering and many other field of science and engineering [2].When the correlation between the optimization and architecture can be found?
This association apparently appeared when the architectural designs problems started to be expressed as the logic structures and functions, since the optimization problems are formulated in the mathematical notifications. The software application for the generative and parametric architectural design enable users to prototype dependencies and relationships between components using the power of math and scripting tools. These tools are relatively new, most of them appeared after 2000 a.d. (drawing 2). Nevertheless, according to Charles Jencks [8], basic rules of parametric design were sketched in mid sixties by Christopher Alexander. This mathematician and architect was first, who proposed making ‘graph theories’ as the representation of an elaborate problem with structural framework of these graphs as a tool to produce solution [7]. Alexander says in his book Notes of the Synthesis of Form: ‘at present we have no corresponding way of simplifying design problems (…), the analysis of the problem is by no means obviously possible’ [1]. In this quotation the ‘means’ could be directly translated as tools. At that time computer programming was in its infancy so that nobody could have been convinced then that computers would become these tools.
Therefore, the basics of parametric design was sketched in 1964 by Christopher Alexander in his book Notes of the Synthesis of Form. At the same time, the optimization found its practical application , since the computer became available in the sixties [5]. As the result, the origins of the optimization applied in architecture may be dated in the 1960s.
For representation of the applied optimization in architecture in the internet resources the new abbreviation "ADO" appeared: "Architectural design optimization (ADO) is a subfield of engineering that uses optimization methods to study, aid, and solve architectural design problems ".
A modern architect, especially one specialized in parametric design uses the computational mathematics on a daily basis. The new software applications let designers to conduct in-depth analysis and define design by scripting tools. Architectural Design Optimization slowly appears in the architectural world. Diverse methods, such as genetic algorithms, artificial intelligence, and more ways of optimization through the algorithms, are introduced into process of design. What architecture can win through the application of the optimization? Adrian Beukers and Ed van Hinte say in their essay Lightness: " in nature shape is cheaper than material ". They mean that the cost of the optimized shape could be far more cheap, if we find the optimal structural and topological solutions. In mega-constructions the possible savings of applied material can be up to 50 percent [6].
Structure and material optimization is only a single possibility in the whole spectre. Generally optimization is extremely helpful in studying, aiding, and solving architectural design problems, such as daylight availability, circulation, optimal floor plan layouts, air circulation, adaptation of projects to law restrictions, cost-effectiveness, energy consumption, visibility, mixes of all these criteria and many others. To make the Architectural Design Optimization a widely used tool in architectural practice, one condition needs to be met: an architect should become a programmer.
References
- Alexander, C. (1964) Notes of the Synthesis of Form, Cambridge Massachusetts: Harvard University Press
- Boyd, S., Vandenberghe, L.(2004). Convex Optimization, Cambridge University Press.
- Dutta, J. Optimization Theory-A Modern face of Applied Mathematics
- Ben-Tal, A. , Nemirovski, A. (2013) Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications; Georgia Institute of Technology, Israel Institute of Technology
- Cherakaev A. (2001), Topics in Applied Math: Methods of Optimization - online course Spring 2001 http://www.math.utah.edu/~cherk/teach/opt/course.html [accessed online 3.01.2014]
- Jaworski P., Piasecki M. (2009) Projektowanie komputacyjne 23.10.2009r. Westval, Szczecin, Poland
- Steadman, P. (2008) The evolution of designs: biological analogy in architecture and the applied arts, a revised edition, New York, Abingdon: Routledge
- Zeszyty Naukowe Politechniki Śląskiej. Architektura (1991)tom. 17, Gliwice: Wydawnictwo Politechniki Śląskiej
