Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

ОПТИМИЗАЦИЯ РАЗМЕЩЕНИЯ ЦЕНТРОВ ОБРАБОТКИ СТАНЦИЙ И ПРЕДПРИЯТИЙ ПО ОБРАБОТКЕ ЖИВОТНОВОДЧЕСКОЙ ПРОДУКЦИИ

Научная статья
Садигова М.Ш.
DOI:
https://doi.org/10.23670/IRJ.2021.108.6.079
Выпуск: № 6 (108), 2021
Опубликована:
2021/06/17
PDF

ОПТИМИЗАЦИЯ РАЗМЕЩЕНИЯ ЦЕНТРОВ ОБРАБОТКИ СТАНЦИЙ И ПРЕДПРИЯТИЙ ПО ОБРАБОТКЕ ЖИВОТНОВОДЧЕСКОЙ ПРОДУКЦИИ

Научная статья

Садигова М.Ш.*

ORCID: 0000-0001-8707-7040,

Гянджинский Государственный Университет, Гянджа, Азербайджан

* Корреспондирующий автор (sadixovametanet[at]mail.ru)

Аннотация

Целью статьи является повышение эффективности управления производством и транспортировкой производственных и перерабатывающих хозяйств за счет обеспечения оптимального транспорта и использования транспортировки продукции животноводства к перерабатывающим предприятиям и пунктам снабжения.

Используемые методология и методы Теоретической и методологической основой исследования послужили работы местных и зарубежных ученых по размещению производственных мощностей, транспорта, а также эксплуатации транспортной системы сбора, статистике, теории вероятностей, графикам и управлению, научной литературе. по экономико-математическому моделированию.

Основным научным нововведением является формирование базы данных расположения точек снабжения и перерабатывающих предприятий на основе закономерностей изменения ключевых показателей, характеризующих транспортировку сырья, и создание оптимальных математических и функциональных моделей согласования интересов всех участников. в транспортной системе.

Результатом исследования является согласование интересов всех участников процесса перевозки продукции животноводства, применение пунктов снабжения и предприятий переработающие этой продукции, а также крупных животноводческих хозяйств для повышения эффективности перевозок при выборе схем транспортировки. Также разработанные математические модели могут быть использованы на практике и при обучении специалистами и руководителями предприятий в сфере транспортировки животноводческой продукции.

Ключевые слова: фермерские хозяйства, перерабатывающие предприятия, продукция животноводства, оптимизация, производственно-перерабатывающий комплекс.

OPTIMIZATION OF LOCATION CENTERS OF PROCESSING STATIONS AND PROCESSING ENTERPRISES FOR LIVESTOCK PRODUCTS

Research article

Sadıgova M.S.*

ORCID: 0000-0001-8707-7040,

Doctor of Philosophy on Technology, Ganja State University, Ganja, Azerbaijan

* Corresponding author (sadixovametanet[at]mail.ru)

Abstract

The purpose of the article is to increase the efficiency of production and transportation management of production and processing farms by providing optimal transport and use of transportation of livestock products to processing enterprises and supply points.

Methodology and methods used Theoretical and methodological basis of the research was the works of local and foreign scientists on the location of production facilities, transportation, as well as the operation of the collection transport system, statistics, probability, graphs and management theories, scientific literature on economic mathematical modeling.

The main scientific innovation is the formation of a database for the location of supply points and processing plants based on the regularities of changes in the main indicators characterizing the transportation of raw materials and the creation of optimal mathematical and functional models of coordination of interests of all participants in the transportation system.

The result of the study is the coordination of the interests of all participants in the process of transportation of livestock products, the application of procurement and processing points and enterprises, as well as large livestock farms to increase the efficiency of transportation when choosing transportation schemes. Also, the developed mathematical models can be used in practice and training by specialists and managers of enterprises in the field of transportation of livestock products.

Keywords: farms, processing enterprises, livestock products, optimization, production-processing complex.

Introduction (problem statement)

There are dozens of processing enterprises processing livestock products in the national market. These enterprises differ from each other in scale, structure, range of products, technological features of production.

As an example, let's formulate the general features of the activity of dairy processing enterprises in the republic:

  1. Lack of resources and unequal access to raw materials.
  2. Inability to store raw materials and products for a long time.
  3. Lack of convenient location of milk processing plants in the area in relation to producers and consumers.
  4. Large number of producers and meeting demand in a short time.
  5. Small batch of raw product.

Thus, modern large milk processing plants combine several links of the transport chain, for example, production and sales links. In such multifunctional enterprises, it is important to ensure synchronization, taking into account all the items and elements of the transport chain, the interrelationships and limitations between them. Therefore, the optimal location of processing plants is the main object that ensures the synchronization of all elements of the transport chain.

Thus, increasing milk production and processing of milk produced in the region should be considered a problem of state importance.

A scientifically based solution to this problem will allow meeting the population's demand for milk and dairy products through local production.

Theoretical research used elements of system analysis, statistics, optimal placement of production capacity, research of operations, probability, mass service theories.

Representation main text

In recent years, publications on the subject have focused on the problems of transportation, production and delivery of livestock products from farms to processing enterprises. In this regard, Kiryakov A.G In the research work “Reproduction of innovations in a market economy” the issues of transportation of livestock products to processing enterprises and supply points were considered [5, P. 88].

Issues of optimal placement of the processing plant and minimization of transportation costs to the enterprise Sadikhova M.Sh. Investigated in the article “Factors of location of the enterprise processing livestock products in the area” Ismailov I. I., Sadikhova M. Sh. “Methods of delivering milk from farms to processing enterprises and parameters of vehicles”, Sadikhova M. Sh., Ismailov I. I. “Optimal location of processing enterprises and centers for stocking livestock products” [11, P. 166], [4, P. 122], [10, P. 47].

Forms of selection of the objective function of the problem of optimization are given in the scientific works of Ivanovsky P. “Theory of probabilities and mathematical statistics” [3, P. 405].

Bowersox D.J, Kloss J.J, “Logistics. Integrated supply chain” and Okhorzin V.A “Optimization of economic systems. Examples and Algorithms in Mathcad” is considered to be the economic region where livestock farms are located and the factors characterizing the construction and location of the mathematical model of the location of the processing plant in the economic region are considered in terms of the specificity of this model [2, P. 51], [8, P. 88].

The presentation of the main material consists of the optimal selection of supply points and processing centers for livestock products.

Determining the optimal location of large industrial complexes is of great economic and technological significance. In particular, the determination of the optimal location centers of large complexes that process the products of agricultural enterprises and farms is a very important issue in modern times. As it is known, such types of problems belong to the category of optimization problems and can be solved by optimization methods.

In order to ensure the transportation of the main livestock products produced by farms in a particular region to the primary processing enterprises and supply points at a minimum cost, the issue of optimal location of processing enterprises in the area should be addressed. The main livestock products are meat, milk, wool and eggs etc. These products are divided into products that are perishable and can be stored under certain conditions, as is known for their shelf life. Therefore, the approach here should be to transport perishable products, milk and meat to processing plants, and eggs and wool to supply points [5, P. 88]. As noted, the main condition for the optimal placement of the processing plant is the minimum cost of transporting the product to the plant. This is possible provided that the distances between the points of production of the product to be transported and the processing plant are kept to a minimum. That is, the processing plant should be located in the area in such a way that it is at an optimal distance from all production facilities. [11, P. 166], [1, P. 27], [4, P 122].

One or more possible variants of such a complex problem can be sought. The region can be considered as a whole or the optimal options can be explored by dividing it into separate parts.

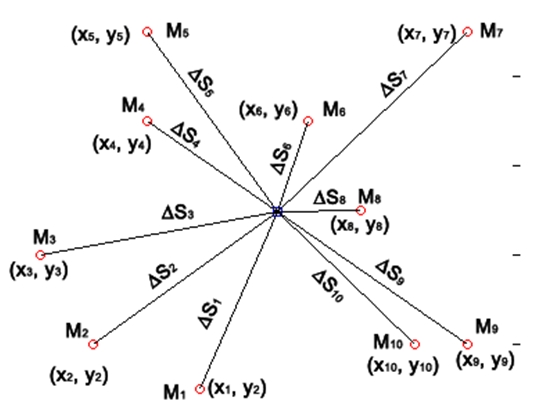
The general algorithm of the optimization problem is given in Figure 1.

11-07-2021 11-00-09

Fig. 1 – Algorithm for selection of the optimal center of the processing plant and supply point in the plane in the geographical local area

 

11-07-2021 11-01-06 - are the places on the map of the regions where livestock products are produced in the studied area;

11-07-2021 11-01-15 – is the distance from the optimal location center to be determined to the i district center;

11-07-2021 11-01-33 - are the coordinates of the district centers on the map;

11-07-2021 11-01-59 - is the number of regions where livestock products are produced.

According to the problem, it is required to minimize the total distance to the center, where the processing plant and the point of supply of livestock products are optimally located. Therefore, the objective function of the optimization problem is selected in the following form: [1, P. 27], [3, P. 405].

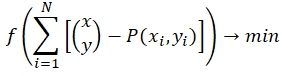11-07-2021 11-05-11     (1)

Here 11-07-2021 11-01-59 - are the points where the product is transported, the regions;

x and y are the unknown coordinates of the center where the processing plant and the supply point will be located;

11-07-2021 11-05-39 – are the coordinates of each district center producing livestock products known from the map;

(1) indicates the minimization of the total distance of transportation from all district centers producing livestock products in the region to the center where the optimal location will be determined.

As you know, there must be limits to every optimization (In some cases, there may be no restrictions). In the complex issue we are considering, in general, the restrictions must have an economic meaning. Therefore, the restrictions can be formulated as follows [8, P. 120], [9, P. 24]:

 11-07-2021 11-07-55    (2)

Here: 11-07-2021 11-10-02 - is the purchase price of agricultural products, raw materials from the producer, manat; (AZN)

s - cost per unit of product made from raw materials, manat; (AZN)

11-07-2021 11-10-16 - is a portable raw material;

11-07-2021 11-10-44 -is total, 11-07-2021 11-10-16 – Transportation cost of 1 km of livestock products from the producer farm to the processing enterprise-center, man 11-07-2021 11-11-06/ tkm;

 11-07-2021 11-14-54 – is the length of the straight line from the processing plant i and the supply point to the production point in the coordinate to be determined 11-07-2021 11-15-11;

11-07-2021 11-15-26 – coefficient of variation of quantitative 11-07-2021 11-10-16 raw materials in the technological process (decrease or increase, this price can be taken as an equal constant price in the first approximation, 11-07-2021 11-15-44;

11-07-2021 11-16-18 – is the selling price of a product made from raw materials at a processing plant, manat.

Thus, the mathematical expression of the optimization function and constraint conditions for the optimal location of the processing plant and supply point for the transportation of livestock products can be described as follows:

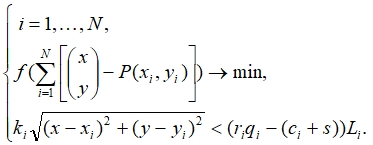11-07-2021 11-27-21   (3)

It should be noted that the coordinates of the regions producing livestock products should be taken from the map and calculated on a scale. In this case, in order to reduce the errors, the coordinate center (it means, the calculation point (0, 0)) should be taken in the largest industrial center of the region and a coordinate matrix should be compiled.

The purpose function in determining the optimal placement center of a milk processing plant is expressed as follows:

11-07-2021 11-27-29    (4)

The final mathematical expression for the optimal location of the milk processing plant and the meat supply point will be as follows:

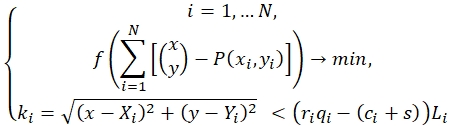11-07-2021 11-27-40     (5)

Now let`s look at a concrete example of the construction of a mathematical model of dairy farms and processing plants.

The problem of locating a production and processing complex in a specific area depends on the climate of production conditions, soil quality, etc. the difference is due to the location of production capacity, including labor resources.

The location model of the production and processing complex envisages the possibility of transportation of transportable materials and favorable distribution of financial resources between the territories.

The object of the model is the economic region where livestock farms are located. From the point of view of the specificity of the model, let`s consider the factors characterizing the construction and placement of the mathematical model of the location of the processing plant in the territory of the economic region: [2, P. 51], [8, P. 88].

-Possibility of processing livestock products produced in the area at the processing plant;

-Placement of means of production;

-Placement of production resources, possibility of product transportation;

-Financial resources of producers and processing enterprises;

-Possibilities of sales bases for processing of livestock products;

-Transportation costs during transportation

The location of livestock processing facilities should be taken into account when determining:

- Availability of labor resources, working capital and financial security of cattle, pastures, means of production of producer farms and processing enterprises;

-Technological capabilities of participating enterprises;

-Possibility of transportation of products to processing and supply points;

- Possibility of participating enterprises to provide mutual financial assistance;

- Presence of the minimum required level of profitability of production in the participating enterprises.

These conditions must ensure the maximum income from the economic activities of the “farm-processing enterprise” complex.

Thus, considering the factors characterizing the construction and placement of the mathematical model of the location of the processing plant in the economic region, let`s consider the mathematical description of the elements included in the mathematical model of the “farm-processing plant” complex [12, P. 293].

The first element of the model is a livestock farm that produces livestock products for the next element of the model.

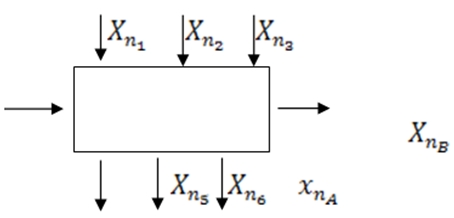
The mathematical description of the variables of the model of livestock farms (n) can be expressed as follows [6, P. 26].

11-07-2021 11-32-06 -number of head cattle, head; 11-07-2021 11-32-13 - direction of investment activity in animal husbandry, thousand manat; 11-07-2021 11-32-21 - realization of livestock products outside the complex, t; 11-07-2021 11-32-27 - domestic financial transactions, thousand manat; 11-07-2021 11-32-35 - taxes, thousand manat; 11-07-2021 11-32-44 - purchase of mixed feeds, man / t; 11-07-2021 11-32-51 - current production costs, thousand man; 11-07-2021 11-32-59 - income from the sale of the responsible, thousand man.

11-07-2021 11-31-02

Fig. 2 – Structural model of livestock farms

 

The result of the study is the coordination of the interests of all participants in the process of transportation of livestock products, the application of procurement and processing points and enterprises, as well as large livestock farms to increase the efficiency of transportation when choosing transportation schemes. Also, the developed mathematical models can be used in practice and training by specialists and managers of enterprises in the field of transportation of livestock products. 

Конфликт интересов Не указан. Conflict of Interest None declared.
 

Список литературы / References

  1. Алиев К.И. Определение оптимального центра размещения объектов в вычислительной системе MATHCAD / К.И. Алиев, С.Т. Гусейнов // Аграрная Наука, Москва, 2007, с. 27-30
  2. Бауэрсокс Д.Дж. Логистика. Интегрированная цепь поставок / Д.Дж. Бауэрсокс, Д.Дж. Клосс. М., Олимп – бизнес, 2010, c.51
  3. Ивановский P. Теория вероятностей и математическая статистика. Основы, прикладные аспекты с примерами и задачами в среде Mathcad / P. Ивановский. М.: БХВ-Петербург, 2008, с.405
  4. Исмаилов И. И. Cпособы доставки молока из ферм на перерабатывающие предприятия и параметры транспортных средств / И. И. Исмаилов, М. Ш. Садыхова // AMEA, Gəncə bölməsi “Xəbərlər məcmuəsi” № 1(59), 2015, s. 122-126.
  5. Кирьяков А. Г. Воспроизводство инноваций в рыночной экономике. (Теоретико-методологический аспект) / А. Г. Кирьяков. Ростов на Дону. Издательство РГУ 2005-c.88
  6. Кормаков Л. Ф. Экономическая эффективность аграрных технико-технологических проектов: вопросы методологии её оценки / Л. Ф. Кормаков, Л. С. Орсик // Экономика сельскохозяйственных и перерабатывающих предприятий, 2005, №1, с. 26-29
  7. Охорзин В. А. Компьютерное моделирование в системе Mathcad / В. А. Охорзин. М.: Финансы и статистика, 2006, с.120-136
  8. Охорзин В. А. Оптимизация экономических систем. Примеры и алгоритмы в среде Mathcad / В. А. Охорзин. М.: Финансы и статистика, 2005, с. 88
  9. Поршнев С. В. Численные методы на базе Mathcad (+ CD) / С. В. Поршнев, И. В. Беленкова. С-Пб: БХВ-Петербург, 2005, с.24-26 ISBN: 5-94157-610-2.
  10. Садыхова М.Ш. Оптимальное размещение перерабаты-вающих предприятий и центров заготовки животноводческой продукции / М.Ш. Садыхова, И.И. Исмайлов // Вестник Российского Государственного Аграрного Заочного Университета. Научный журнал №24(29) Mосква 2017, с. 47-53.
  11. Sadıxova M.Ş. Ərazidə heyvandarlıq məhsulları emal edən müəssisənin yerləşdirilməsinin amilləri / M.Ş. Sadıxova // ADAU Beynəlxalq Elmi- Praktiki Konfrans 22-24 sentyabr, II cild, Gəncə, 2014, s. 166-169
  12. Sadıxova M.Ş. Heyvandarlıq məhsullarının emal müəssisələrinə daşınmasında iqtisadi-riyazi modelləşdirmə / M.Ş. Sadıxova // ADAU 8-Beynəlxalq Elmi- Praktik Konfransın materialları 03-04 oktyabr 2016, Gəncə, II cild, s. 293-295

Список литературы на английском языке / References in English

  1. Aliev K.I. Opredelenie optimal'nogo centra razmeshhenija ob’ektov v vychislitel'noj sisteme MATHCAD [Determination of the optimal center for placing objects in the MATHCAD computing system] / K.I. Aliev, S.T. Gusejnov // Agrarnaja Nauka [Agrarian Science], Moscow, 2007, p. 27-30 [in Russian]
  2. Bowersox D.J. Logistika. Integrirovannaja cep' postavok [Logistics. Integrated supply chain] / D.Dzh. Baujersoks, D.Dzh. Kloss, Moscow, Olymp - business, 2010, p. 51 [in Russian]
  3. Ivanovsky P. Teorija verojatnostej i matematicheskaja statistika. Osnovy, prikladnye aspekty s primerami i zadachami v srede Mathcad [Probability theory and mathematical statistics. Basics, applied aspects with examples and tasks in the Mathcad environment] / P. Ivanovskij. Moscow: BHV-Petersburg, 2008, p. 405 [in Russian]
  4. Ismailov I. I. Cposoby dostavki moloka iz ferm na pererabatyvajushhie predprijatija i parametry transportnyh sredstv [Methods for delivering milk from farms to processing enterprises and parameters of vehicles] / I. I. Ismailov, M. Sh. Sadyhova // AMEA, Gəncə bölməsi “Xəbərlər məcmuəsi” [ANAS, Ganja branch “News bulletin”] № 1 (59), 2015, p. 122-126. [in Russian]
  5. Kiryakov A. G. Vosproizvodstvo innovacij v rynochnoj jekonomike. (Teoretiko-metodologicheskij aspekt) [Reproduction of innovations in a market economy. (Theoretical and methodological aspect)] / A. G. Kir'jakov. Rostov on Don. Publishing house RSU 2005-p.88 [in Russian]
  6. Kormakov L. F. Jekonomicheskaja jeffektivnost' agrarnyh tehniko-tehnologicheskih proektov: voprosy metodologii ejo ocenki [Economic efficiency of agrarian technical and technological projects: questions of methodology for its assessment] / L. F. Kormakov, L. S. Orsik // Jekonomika sel'skohozjajstvennyh i pererabatyvajushhih predprijatij [Economy of agricultural and processing enterprises], 2005, №1, p. 26-29 [in Russian]
  7. Okhorzin V.A. Komp'juternoe modelirovanie v sisteme Mathcad [Computer modeling in the Mathcad system] / V. A. Ohorzin. Moscow: Finance and statistics, 2006, p. 120-136 [in Russian]
  8. Okhorzin V. A. Optimizacija jekonomicheskih sistem. Primery i algoritmy v srede Mathcad [Optimization of economic systems. Examples and algorithms in the Mathcad environment] / V. A. Ohorzin. Moscow: Finance and statistics, 2005, p. 88 [in Russian]
  9. Porshnev S. V. Chislennye metody na baze Mathcad (+ CD) [Numerical methods based on Mathcad (+ CD)] / S. V. Porshnev, I. V. Belenkova. St. Petersburg: BHV-Petersburg, 2005, pp. 24-26 ISBN: 5-94157-610-2. [in Russian]
  10. Sadikhova M.Sh. Optimal'noe razmeshhenie pererabaty-vajushhih predprijatij i centrov zagotovki zhivotnovodcheskoj produkcii [Optimal location of processing enterprises and centers for the procurement of livestock products] / M.Sh. Sadyhova, I.I. Ismajlov // Vestnik Rossijskogo Gosudarstvennogo Agrarnogo Zaochnogo Universiteta. Nauchnyj zhurnal [Bulletin of the Russian State Agrarian Correspondence University. Scientific journal] №24 (29) Moscow: 2017, p. 47-53. [in Russian]
  11. Sadikhova M.Sh. Ərazidə heyvandarlıq məhsulları emal edən müəssisənin yerləşdirilməsinin amilləri [Factors of location of the enterprise processing livestock products in the area] / M.Ş. Sadıxova // ADAU Beynəlxalq Elmi- Praktiki Konfrans 22-24 sentyabr [ASAU International Scientific-Practical Conference September 22-24], Vol. II, Ganja, 2014, p. 166-169 [in Azerbaijanian]
  12. Sadikhova M.Sh. Heyvandarlıq məhsullarının emal müəssisələrinə daşınmasında iqtisadi-riyazi modelləşdirmə [Economic-mathematical modeling in the transportation of livestock products to processing enterprises] / M.Ş. Sadıxova // ADAU 8-Beynəlxalq Elmi- Praktik Konfransın materialları 03-04 oktyabr 2016 [Materials of the 8th International Scientific-Practical Conference ASAU], 03-04 October 2016, Ganja, Vol. II, p. 293-295 [in Azerbaijanian]