СИНТЕЗ ЛИНЕЙНО-КВАДРАТИЧНЫХ ЗАКОНОВ УПРАВЛЕНИЯ ДЛЯ НЕПРЕРЫВНЫХ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
Быстров С.В.1, Григорьев В.В.2, Першин И.М.3, Мансурова О.К.4
1ORCID: 0000-0002-6900-0506, Кандидат технических наук, 2ORCID: 0000-0001-8374-1899, Доктор технических наук, Санкт-Петербургский национальный исследовательский университет информационных технологий механики и оптики, г. Санкт-Петербург, 3ORCID: 0000-0002-7618-1173 , Доктор технических наук, Северо-Кавказский федеральный университет филиал г. Пятигорск, 4ORCID: 0000-0002-3169-3431 Кандидат технических наук, Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург
Статья подготовлена по результатам работы, выполненной при государственной финансовой поддержке ведущих университетов Российской Федерации (субсидия 074-U01) Министерства образования и науки РФ (проект 14.Z50.31.0031)
СИНТЕЗ ЛИНЕЙНО-КВАДРАТИЧНЫХ ЗАКОНОВ УПРАВЛЕНИЯ ДЛЯ НЕПРЕРЫВНЫХ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
Аннотация
Для непрерывных линейных динамических объектов с одним входом и выходом разработана процедура синтеза полиномиальных, в частности линейно квадратичных законов управления позволяющих повысить скорость сходимости процессов при больших отклонениях с сохранением качественных показателей процессов при малых отклонениях, присущих широко используемым линейным законам управления. Синтез законов управления производится на основе использования методов теории оптимального управления посредством решения уравнения типа Риккати. Доказывается, что используемые законы управления не нарушают свойства асимптотической или экспоненциальной устойчивости, в зависимости от выбранного типа устойчивости при проектировании.
Ключевые слова: линейно квадратичные законы управления, критерии оптимальности. экспоненциальная устойчивость, матричные уравнения Риккати и Ляпунова.
Bystrov S.V.1, Grigoriev V.V.2, Pershin I.M.3, Mansurova O.K.4
1ORCID: 0000-0002-6900-0506, PhD in Engineering, 2ORCID: 0000-0001-8374-1899, PhD in Engineering, ITMO University, St. Petersburg, 3ORCID: 0000-0002-7618-1173, PhD in Engineering, Severo -Kavkazsky Federal University branchin in Pytigorsк, 4ORCID: 0000-0002-3169-3431, PhD in Engineering National Mineral Resources University (Mining University) , St. Petersburg
SYNTHESIS OF LINEAR-QUADRATIC CONTROL LAWS FOR CONTINUOUS DYNAMIC OBJECTS
Abstract
For continuous linear dynamic objects with a single inlet and outlet linear quadratic synthesis procedure of control laws was designed. The use of these control laws can improve the speed of convergence processes for large deviations while maintaining quality indicators processes for small deviations. Synthesis of control laws is based on the use of methods of optimal control theory by solving the Riccati type equation. It is proved that the used control laws do not violate the property of asymptotic and exponential stability, depending on the type of stability in design.
Keywords: linear quadratic control laws, optimality criteria, exponential stability, matrix Riccati and Lyapunov equations.
Методы теории оптимального управления широко используются для синтеза линейных законов управления непрерывными стационарными объектами, обеспечивающих тот или иной вид устойчивости замкнутой системы, а следовательно и требуемые показатели качества [1, с. 586], [2, С. 170], [3, С. 15], [4, С. 32]. В данной работе предпринята попытка распространения этих методов для формирования полиномиальных законов управления для непрерывных стационарных объектов управления с целью повышения скорости сходимости процессов при больших начальных отклонениях с последующим замедлением сходимости при малых отклонениях для обеспечения таких качественных показателей как перерегулирование, колебательность процессов. Для решения задачи синтеза управлений используется модифицированное уравнение типа Риккати, позволяющее искать управление как линейную функцию состояний объекта, которое и используется для формирования полиномиальных управляющих воздействий. Доказывается, что подобные управления сохраняют свойство асимптотической или экспоненциальной устойчивости, в зависимости от того какой вид устойчивости был заложен при поиске линейного закона управления при решении уравнения Риккати.
Рассмотрим линейный непрерывный стационарный объект управления (ОУ) с уравнением движения
![]() (1)
(1)
где x – n - мерный вектор состояния ОУ, u – скалярное управляющее воздействие, А - квадратная матрица с постоянными коэффициентами размером n х n, B - матрица входов размером n х 1. Будем искать закон управления в виде
![]() (2)
(2)
где K – матрица линейных стационарных обратных связей (ЛСОС) размерности 1 х n, элементы которой определяют коэффициенты обратных связей по соответствующим переменным вектора состояний x(t).
Ставится задача отыскания таких матриц ЛСОС с использованием методов теории оптимального управления, которые в замкнутой системе для объектов управления (1) с законами управления вида (2) обеспечивают экспоненциальную устойчивость тесно связанную с таким показателем качества процессов как быстродействие (время переходного процесса).
Основной результат
Нахождение линейного закона управления с использованием методов теории оптимального управления для стационарного непрерывного объекта управления (1) с квадратичным критерием качества на бесконечном интервале времени сводится к решению матричного квадратичного уравнения типа Риккати вида
![]() (3)
(3)
при
![]() (4)
(4)
где P – симметрическая квадратная матрица размером n х n, Q – симметрическая матрица штрафов на вектор состояния объекта размером n х n, по крайней мере положительно полуопределенная, R – ненулевой скаляр, определяющий штраф на управление, v – параметр, принимающий значения в пределах от 0 до 2. Уравнение (3) при подстановке в него (4) является квадратичным уравнением Риккати, имеющим два решения относительно матрицы P, из которых выбирается положительно определенное решение, то есть такое решение, при котором матрица P является положительно определенной матрицей.
Заметим, что при значении параметра v = 0 уравнение (3) превращается в линейное уравнение типа Ляпунова и его решение относительно матрицы P будет положительно определенным тогда и только тогда, когда матрица A является устойчивой матрицей, то есть объект управления устойчив. Этот случай соответствует критерию обобщенной работы для нахождения оптимального управления, введенный в работах Красовского А.А..
При значении параметра v = 1 получаем уравнение типа Риккати, соответствующее классическому решению задачи оптимального управления, для которого доказано, что одно из решений уравнения Риккати положительно определено (матрица P - положительно определенная матрица и замкнутая система с матрицей ЛСОС (4) будет устойчивой).
Если значение параметра v = 2 , то уравнение Риккати позволяет решать задачу нахождения оптимального управления, соответствующего принципу оптимальности по принуждению [2, С. 56 ]. Отметим, что при этом, уравнение Риккати при данном значении параметра v совпадает с уравнением Ляпунова для замкнутой системы с найденным управлением, позволяющим делать заключение, что если решение уравнения Риккати положительно определено, то система будет асимптотически устойчивой.
Для того чтобы линейный закон управления обеспечивал бы экспоненциальную устойчивость со степенью сходимости α, модифицируем уравнение (3) следующим образом
![]() (5)
(5)
при
![]() (6)
(6)
Заметим, что при значении v = 0 требуется, чтобы исходный объект был бы экспоненциально устойчивым со значением степени сходимости, равным α. В дальнейшем, основное внимание уделим случаю, когда значение параметра v = 2, то есть когда уравнение (6) является модифицированным уравнением Ляпунова для установления факта, что система с искомым управлением является экспоненциально устойчивой.
Докажем теперь, что если найден закон управления (7) на основании решения уравнения Риккати (6) с заданным значением степени сходимости α, то линейно квадратичный закон управления вида (2) обеспечивает в замкнутой системе экспоненциальную устойчивость со степенью сходимости равной α.
Положим, что матрица ЛСОС K найдена по выражению (7) в результате решения уравнения Риккати (6) при заданном значении степени сходимости α. Вычислим производную по времени от квадратичной функции Ляпунова на всех траекториях движения системы (объект управления (1) с законом управления вида (2)) и проверим, будет ли выполняться условие экспоненциальной устойчивости [2, С. 24]
![]() (7)
(7)
а P положительно определенная матрица, являющаяся решением матричного уравнения типа Риккати (6). Производная от функции Ляпунова для замкнутой системы (объект управления (1) с законом управления (2) ) имеет вид
![]()
Воспользуемся тем, что матрица K закона управления вычисляется по соотношению (6), тогда выражение для производной от функции Ляпунова можно привести к виду
![]()
Если матрица P, определяющая квадратичную функцию Ляпунова (8), найдена как положительно определенное решение уравнения Риккати (6), при значении параметра v = 2 и с заданной степенью сходимости α, то выполняется равенство
![]()
а так как выражение ![]() , по крайней мере, положительно полуопределено, справедливо неравенство
, по крайней мере, положительно полуопределено, справедливо неравенство
![]() (9)
(9)
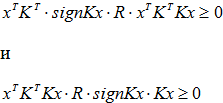
по крайней мере, положительно полуопределены, то их добавление в неравенство (9) может только усилить это неравенство, откуда следует выполнение неравенства
![]() (10)
(10)
что подтверждает выполнение условия экспоненциальной устойчивости со степенью сходимости равной α.
И так, последовательность процедуры синтеза линейно квадратичных законов управления (2), обеспечивающих экспоненциальную устойчивость, заключаются в следующем. По заданному требованию к быстродействию замкнутой системы, например, по требуемому времени переходного процесса tп выбирается заданная степень сходимости процесса по соотношению
Далее решается матричное уравнение Риккати (6) относительно матрицы Р с последующим вычислением матрицы K по выражению (7) , в результате формируется закон управления вида (2).
Заключение
Предложена процедура вычисления линейно-квадратичных законов управления на основе использования методов теории оптимального управления, обеспечивающих экспоненциальную устойчивость с заданной степенью сходимости процессов, назначаемую по требуемому быстродействию системы. Для оценки качества процессов и построения областей, в которых выполняются эти показатели можно использовать результаты статей [5, С. 2].
Перспективным является использование подобных управлений в системах пространственного слежения, в которых при наличии нелинейности на входе объекта имеющей при больших отклонениях нисподающий участок пеленгационной характеристики квадратичная составляющая закона управления позволяет ускорить сходимость процессов, а также для систем с распределенными параметрами [6, С. 2].
Список литературы / References
- Nair G.N. Evans R.I. Exponential stabilisability of finite-dimensional linear systems with limited data rates / G.N. Nair, R.I. Evans // Automatica. –2003. – Vol. 39. – P. 585–593. doi:10.1016/j.automatica.
- Фурасов В.Д. Устойчивость движения, оценки и стабилизация /В.Д. Фурасов – М.: Наука, 1977. – 247 с. doi: 10.17117/cn.2015.01.07
- Bystrov S.V., Grigoriev V.V. Qualitative Exponential Stability and Instability of Dynamical Systems and Range Estimation of Parameter Acceptable Changes / S.V. Bystrov, V.V. Grigoriev // Universal Journal of Control and Automation. – 2013. – Vol. 1. – N 1. – P. 15–18. doi: 10.13189.
- Быстров С.В., Григорьв В.В., Рабыш Е.Ю., Мансурова О.К. Анализ качества переходных процессов в непрерывных и дискретных системах на основе условий качественной экспоненциальной устойчивости / С.В. Быстров, В.В. Григорьв, Е.Ю. Рабыш, О.К. Мансурова // Мехатроника, Автоматизация, Управление. – М., – 2012. – № 9. – С. 32–36.
- Бобцов А.А., Быстров С.В., Григорьев В.В., Мансурова О.К. Построение областей допустимых изменений параметров гарантированного качества процессов динамических систем / А.А. Бобцов, С.В. Быстров, В.В. Григорьев, О.К. Мансурова// Мехатроника, автоматизация, управление. – М., – 2006. – № 10. – С. 2–5.
- Быстров С.В., Григорьев В.В., Мансурова О.К., Першин И.М. Анализ устойчивости линейных систем с распределенными параметрами /С.В. Быстров, В.В. Григорьев, О.К. Мансурова, И.М. Першин // Мехатроника, автоматизация, управление. – М., – 2013. – № 9. – С. 2–5.
Список литературы на английском языке / References in English
- Nair G.N. Evans R.I. Exponential stabilisability of finite-dimensional linear systems with limited data rates / G.N. Nair, R.I. Evans // Automatica. –2003. – Vol. 39. – P. 585–593. doi:10.1016/j.automatica.
- Furasov V.D. Ustojchivost' dvizhenija, ocenki i stabilizacija [Stability of motion, assessment and stabilization] / V.D. Furasov – M.: Nauka, 1977. – 247 p. doi: 10.17117/cn.2015.01.07. [in Russian]
- Bystrov S.V., Grigorv V.V. Qualitative Exponential Stability and Instability of Dynamical Systems and Range Estimation of Parameter Acceptable Changes // Universal Journal of Control and Automation. – 2013. – Vol. 1. – N 1. – P. 15–18. doi: 10.13189.
- Bystrov S.V., Grigorv V.V. Rabysh E.Y., Mansurov O.K. Analiz kachestva perehodnyh processov v nepreryvnyh i diskretnyh sistemah na osnove uslovij kachestvennoj jeksponencial'noj ustojchivosti [Analysis of the quality of transient processes in continuous and discrete systems based on high-quality conditions for exponential stability] // Mechatronics, Automation, Control. – М., – 2012. – № 9. – P. 32–36. [in Russian]
- Bobtsov A.A., Bystrov, S.V., Grigoriev V.V., Dudrov P.V. Kozis D.V., Kostina O.V., Mansurov O.K. Postroenie oblastej dopustimyh izmenenij parametrov garantirovannogo kachestva processov dinamicheskih sistem [Construction areas of acceptable change the parameters of quality assured processes of dynamic systems] // Mechatronics, Automation, Control. № 10. P. 2-5. [in Russian]
- Bystrov S.V., Grigoriev V.V., Mansurova O.K., Pershin I.M. Analiz ustojchivosti linejnyh sistem s raspredelennymi parametrami [Analysis of stability of linear systems with distributed parameters]. Mechatronics, Automation, Control. – М., – 2013. – № 9. – P. 2–5. [in Russian]
