МЕТОДИКА ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
Литвинова Э.В.
ORCID: 0000–0002–6409–9834, Кандидат технических наук, Академия строительства и архитектуры ФГАОУ ВО «Крымский федеральный университет имени В.И. Вернадского»
МЕТОДИКА ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
Аннотация
Предлагается методика оптимального проектирования строительных конструкций с точки зрения обеспечения заданной вероятности их функционирования. Исследование базируется на применении методов программирования, с использованием стохастических моделей загружения строительных конструкций, особенно при внешнем сейсмическом воздействии. Представляется, что предлагаемая методика оптимального проектирования строительных конструкций может дать существенный результат в экономии материальных ресурсов при проектировании и строительстве сооружений различного предназначения.
Ключевые слова: нелинейное и стохастическое программирование, оптимальное решение, функциональные ограничения, ограничения по вероятности.
Litvinova E.V.
ORCID: 0000–0002–6409–9834, PhD in Engineering, Academy of Construction and Architecture Crimean federal university named after V.I. Vernadskogo, Simferopol
METHODOLOGY OF OPTIMAL PLANNING OF BUILDING CONSTRUCTIONS
Abstract
Methodology of the optimal planning of building constructions is offered from the point of view of providing of the set probability of their functioning. Research is based on application of methods of programming, with the use of stochastic models of loading of building constructions, especially at external seismic effect. The offered methodology of the optimal planning of building constructions can give a substantial result in the economy of material resources at planning and building of building of different destiny.
Keywords: nonlinear and stochastic programming, optimal decision, functional limitations, limitations on probability.Системный анализ и теория надежности представляют собой тот математический аппарат, который, кроме прочего, накладывает на проект ряд ограничений исходя из требований к обеспечению безопасной эксплуатации здания или сооружения в течение некоторого расчетного периода.
Системный анализ позволяет все процессы проектирования отдельных элементов строительных конструкций и всего здания в целом связать в единую технологическую цепочку: от рождения идеи о создании строительного объекта до дня прекращения его эксплуатации. Применение системного анализа к проектированию строительных объектов позволяет выделить одинаковые этапы работ для всех типов конструкций, направленные на наилучшее решение поставленных задач и максимально исключающие необъективность [1, 2].
Рассмотрим класс задач, где наилучшее сочетание параметров элементов конструкций оказывается на границе функциональных ограничений (по нагрузкам, габаритам, по прочности и жесткости отдельных элементов конструкции, допустимым отклонениям варьируемых параметров, по стоимости и другие) [3–5].
Если оптимальное решение искать без учета помех методами нелинейного программирования, то это означает, что «практически в 50% случаев будет иметь место отказ системы» [1].
Таким образом, для прогноза развития аварийных процессов, которые могут привести к катастрофическим последствиям, следует применять детерминированные модели этих процессов. При их разработке необходимо стремиться выстраивать систему допущений таким образом, чтобы они приводили к ошибкам в оценках максимальных нагрузок на элементы конструкции в безопасную зону (в сторону их увеличения).
Это относится и к другим факторам, влияющим на безопасность.
В связи с этим актуальным является анализ каркасных конструкций с использованием стохастических моделей их загружения, особенно при динамическом (внешнем сейсмическом) воздействии. Это позволит оптимизировать параметры элементов конструкций и их конфигурацию для любой заданной вероятности их безопасного функционирования.
Рассмотрим разработку методики оптимального проектирования элементов строительных конструкций с учетом случайных факторов, влияющих на надежность создаваемой конструкции.
Введем математические обозначения [6]: ![]() – вектор варьируемых параметров;
– вектор варьируемых параметров; ![]() – оптимальный вектор детерминированной задачи;
– оптимальный вектор детерминированной задачи; 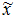 – оптимальный вектор стохастической задачи; θ – вектор случайных параметров;
– оптимальный вектор стохастической задачи; θ – вектор случайных параметров; ![]() – i–я функция ограничения задачи;
– i–я функция ограничения задачи; ![]() – область допустимых решений задачи.
– область допустимых решений задачи.
Пусть необходимо минимизировать функцию
Найдём оптимальное решение ![]() , при котором выполняются условия (2) и (3). Если теперь в модель ввести помехи, то при ее реализации в точке
, при котором выполняются условия (2) и (3). Если теперь в модель ввести помехи, то при ее реализации в точке ![]() ограничения (2) «для одних решений будут выполняться, для других нет» [6]. Таким образом, можно говорить о случайном разбросе функциональных границ вокруг своих номинальных значений.
ограничения (2) «для одних решений будут выполняться, для других нет» [6]. Таким образом, можно говорить о случайном разбросе функциональных границ вокруг своих номинальных значений.
Если, используя выборочные методы, имеется возможность установить законы распределения функциональных ограничений и оценки их параметров в данной точке ![]() , то, задаваясь вероятностью не нарушения границ, можно определить новые функциональные ограничения
, то, задаваясь вероятностью не нарушения границ, можно определить новые функциональные ограничения ![]() , удовлетворяющие выбранному уровню вероятности безотказного функционирования рассматриваемой системы в реальных условиях.
, удовлетворяющие выбранному уровню вероятности безотказного функционирования рассматриваемой системы в реальных условиях.
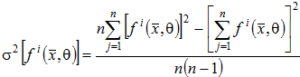 . (5)
. (5)
Необходимо иметь в виду, что по формулам (4) и (5) мы определяем оценки параметров. В задачах, где требуется высокая точность вероятности не нарушения функциональных ограничений, необходим расчет соответствующего объема выборки.
Последовательность оптимизации выделенного класса задач проектирования с использованием их стохастических моделей включает три этапа [6]:
I этап – «поиск оптимального решения на детерминированной модели»;
II этап – «статистический анализ функциональных ограничений в окрестности оптимального решения и построение области допустимых решений задачи по вероятности»;
III этап – «поиск оптимального решения задачи для новой системы функциональных ограничений».
Для применения численных методов исследований сложных строительных конструкций и сооружений целесообразно применять программные комплексы общего назначения. Наряду с этим для расчета уникальных зданий и сооружений могут использоваться программные комплексы, в которых накладываются ограничения на возможность выбора расчетной схемы.
Выделим основные этапы методики оптимального проектирования [6]:
– «разработка математической модели прочности и жесткости элементов конструкции с целью оптимизация ее параметров при действии на нее детерминированной внешней нагрузки»;
– «разработка стохастической модели функционирования конструкции с учетом реальных разбросов (в пределах нормативных допусков) всех случайных параметров для оценки статистических параметров функциональных ограничений и их корректуре».
Рассмотрим пример системного подхода к исследованию каркаса зданий межвидового применения, что дает разнообразие конструктивных схем, воздействий и т.д. [7]. Для эффективного проектирования каркасных конструкций применим расчетную модель, позволяющую точно определить параметры напряженно–деформированного состояния её элементов.
Тогда выделим следующие этапы [7]:
I этап – «разработка расчетной модели каркаса здания, учитывающей факторы, влияющие на напряженно–деформированное состояние элементов»;
II этап – «выявление неизвестных параметров расчетной модели и проведение предварительных вычислений для получения расчетных уравнений»;
III этап – «проведение физических экспериментов для получения данных, необходимых для определения неизвестных параметров расчетной модели и проверки ее адекватности»;
IV этап – «уточнение расчетной модели и выполнение расчетов в необходимом объеме».
Причем результат расчета должен быть получен в виде, удобном для проектирования элементов, а сама расчетная модель должна быть четкой, удобной в работе.
После определения неизвестных параметров были выполнены расчеты модели фрагмента и проверена адекватность расчетной модели, которая показала достоверность разработанной расчетной модели.
На отлаженной расчетной модели были выполнены численные исследования и оценено влияние следующих факторов отклонения: в жесткостных характеристиках элементов, в изменении высоты этажа и граничных условий, в качестве замоноличивания стыков и т.д., на напряженно–деформированное состояние каркаса здания межвидового применения.
Таким образом, при проектировании каркасных сооружений для сейсмоопасных районов выбираются принципиальные конструктивные схемы сооружения; определяются характер и величина распределения усилий и геометрические размеры несущих конструкций от основных загружений; создается расчетная динамическая модель, и находятся возможные динамические усилия (в зависимости от интенсивности землетрясения) в наиболее опасных участках расчетной модели; учитывается возможность их проявления в местах, которые определяют прочность и надежность элементов и их соединений.
Список литературы / References
- Волков А.А. Информационная поддержка процессов оперативного влияния на динамику чрезвычайных ситуаций в строительных объектах / А.А. Волков. – Большой Российский каталог. Строительство. – М.: Каталоги и справочники, 2000. – С. 38–40.
- Volkov A.A. Aktive Sicherheit von Bauobjekten in aussergewhnlichen Situationen // IKM 2000, ABSTRACTS: PROMISE AND REALITY. – Weimar: Bauhaus–Universität Weimar, 2000. – 49 р.
- Волкова В.Н. Основы теории систем и системного анализа / В.Н. Волкова, А.А. Денисов. – СПб.: Изд. СПбГТУ, 1997. – 510 с.
- Лямец В.И. Системный анализ / В.И. Лямец, А.Д. Тевяшев. – Харьков: ХТУРЭ, 1998. – 252 с.
- Петров В.П. Общая теория систем / В.П. Петров, И.С. Сидоров, К.А. Козлов. – СПб.: Научная мысль, 2005. – 480 с.
- Чемодуров В.Т. Моделирование систем / В.Т. Чемодуров. – Л.: ВМА,1983. – 184 с.
- Методические рекомендации по исследованию строительных конструкций с применением математического и физического моделирования. – К: НИИСК,1987. – 68 с.
Список литературы на английском языке / References
- Volkov A.A. Informacionnaja podderzhka processov operativnogo vlijanija na dinamiku chrezvychajnyh situacij v stroitel'nyh ob#ektah [Informative support of processes of operative influence on the dynamics of emergencies in building objects] / A.A. Volkov // Bol'shoj Rossijskij katalog. Stroitel'stvo. [Large Russian catalogue. Building]. – M.: Katalogi i spravochniki [Catalogues and reference books], 2000. – 38–40. [in Russian]
- Volkov A.A. Aktive Sicherheit von Bauobjekten in aussergewhnlichen Situationen // IKM 2000, ABSTRACTS: PROMISE AND REALITY. – Weimar: Bauhaus–Universität Weimar, 2000. – 49 р.
- Volkova V.N. Osnovy teorii sistem i sistemnogo analiza [Bases of theory of the systems and analysis of the systems] / V.N. Volkova, A.A. Denisov. – SPb.: Izd. SPbGTU, 1997. – 510 [in Russian]
- Ljamec V.I. Sistemnyj analiz [Analysis of the systems] / V.I. Ljamec, A.D. Tevjashev. – Har'kov: HTURJE, 1998. – 252 [in Russian]
- Petrov V.P. Obshhaja teorija sistem [General theory of the systems] / V.P. Petrov, I.S. Sidorov, K.A. Kozlov. – SPb.: Nauchnaja mysl', 2005. – 480 [in Russian]
- Chemodurov V.T. Modelirovanie system [Modeling of the systems] / V.T. Chemodurov. – L.: VMA, 1983. – 184 [in Russian]
- Metodicheskie rekomendacii po issledovaniju stroitel'nyh konstrukcij s primeneniem matematicheskogo i fizicheskogo modelirovanija [Methodical recommendations on research of building constructions with the use of mathematical and physical modeling]. – K: NIISK, 1987. – 68 [in Russian]
