МАТЕМАТИЧЕСКАЯ СТАТИСТИКА КАК МЕТОД ОЦЕНКИ ЭФФЕКТИВНОСТИ ИССЛЕДОВАНИЙ
Кинзябулатов Д.З.1, Габдрахманова К.Ф.2
1 Студент 2 курса, 2 кандидат педагогических наук, Уфимский государственный нефтяной технический университет
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА КАК МЕТОД ОЦЕНКИ ЭФФЕКТИВНОСТИ ИССЛЕДОВАНИЙ
Аннотация
В статье рассмотрено применение математической статистики в исследовании производственных процессов, их эффективность, а именно поиск закономерностей величин различных технологических процессов и прогнозирования их изменения.
Ключевые слова: математическая статистика, оценка, анализ, вычисление риска, решение, исследования, прогнозирование, оптимизация.
Kinzyabulatov D.Z.1, Gabdrahmanova K.F.2
1 second-year student, 2 PhD in Pedagogy, Ufa State Oil Technical University
MATHEMATICAL STATISTICS AS A METHOD OF EVALUATING THE EFFECTIVENESS OF RESEARCH
Abstract
The article describes the application of mathematical statistics in the study of the production processes, their efficiency, namely the search for patterns of values of various technological processes and prediction of their changes.
Keywords: mathematical statistics, assessment, solutions, calculation, analysis, prognostication, research, optimization.
Рассмотрим использование элементов математической статистике в исследовании прогнозирования величин, оценки величин и диапазона диагностических критериев, обеспечивающих получение ожидаемого технологического эффекта, которое поможет рассчитать риск. При разработке или эксплуатации скважины данный комплекс мероприятий является важным, так как без прогнозирования и оценки нельзя узнать о содержании в пласте дебита, а также значений величин, необходимых для его добычи (например, глубины бурения или пластового давления).
Решением задач, связанных исследованием закономерностей различных технологических процессов, занимались многие исследователи. Наибольшая заслуга в этом вопросе принадлежит А.Х. Мирзаджанзаце[6]. Достаточно успешные попытки в этом направлении делали и другие исследователи. К примеру, в работе Г.Д. Бревдо “Проектирование режима бурения”[1] представлены монографии по технологии бурения, а в работе Ю.А. Гуторова, А.Ю. Гуторова, Е.В. Вороновой “О механизме формирования остаточных запасов в терригенных коллекторах нефтяных месторождений”[3] – монографии по добыче и эксплуатации нефтяных месторождений. Вопросам исследований, связанных математической статистике, конкретно в нефтегазовом деле, посвящена работа Ю.А. Гуторова, К.Ф. Габдрахмановой, П.А. Ларина[4]. Однако недостаточно рассмотрены методики оптимизации этих процессов на основе полученных данных.
Проведем исследования, с использованием теории математической статистики на Фёдоровском месторождении (Западная Сибирь), которое нам позволит принять решение в выборе технологических методов.
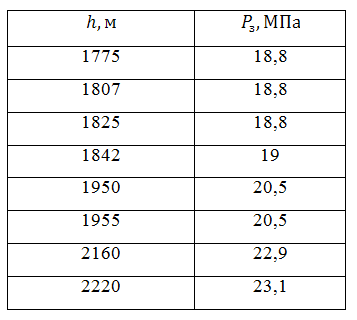
На основе геолого-промысловых исследований имеем следующие значения забойного давления, соответствующие глубине [5]:
С помощью статистического анализа мы можем прогнозировать изменение величины забойного давления от глубины залегания дебита.
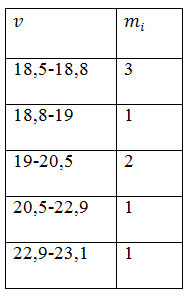
а) Вариационный ряд:
18,8;18,8;18,8;19;20,5;20,5;22,9;23,1.
б) Число интервалов
Длина интервала:
Начало первого интервала:
в) Шкала интервалов:
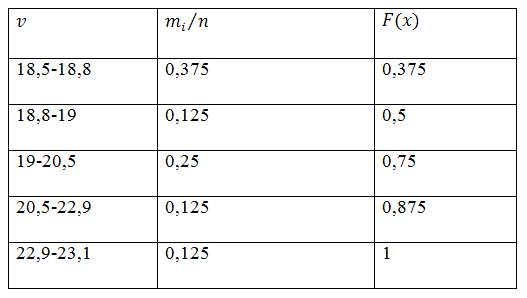
г) Вариационный ряд частностей:
д) Математическое ожидание:
Далее находим дисперсию:
где
Для величины пластового давления ![]() . Следовательно, среднее математическое отклонение
. Следовательно, среднее математическое отклонение ![]() Находим коэффициент вариации:
Находим коэффициент вариации:
Исходя из полученного значения коэффициента, можно сделать вывод, что совокупность является однородной.
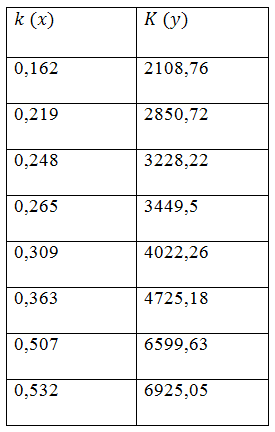
Теперь проведём корреляционный анализ для того, чтобы выяснить значимость коэффициента корреляции между коэффициентом проницаемости и коэффициентом продуктивности.
Мы вычислили значение продуктивности для каждого значения проницаемости:
Далее находи средние значения:
Средние квадратические отклонения величин:
Затем находим выборочную ковариацию:
Выборочный коэффициент корреляции:
Для проверки гипотезы ![]() :
: ![]() используем преобразование Фишера:
используем преобразование Фишера:
Далее,
Задавшись ![]() , по специальной таблице для вероятности
, по специальной таблице для вероятности ![]() берём
берём ![]() и
и ![]()
Поскольку выполняется неравенство ![]() , т.е.
, т.е. ![]() , гипотеза
, гипотеза ![]() :
: ![]() принимается.
принимается.
Вывод:
Из проведенных расчетов видно, что математическая статистика является мощным аппаратам при проведении исследований в разных областях. В частности, при помощи данных расчётов возможно прогнозировать эффективность проведённых работ процессов бурения.
Литература
- Бревдо Г.Д. Проектирование режима бурения. М. Недра, 1988, 200 с.
- Ганджумян Р.А. Математическая статистика в разведочном бурении: Справочное пособие. М.: Недра, 1990. 218 с.
- Гуторов Ю.А., Гуторов А.Ю., Воронова Е.В. О механизме формирования остаточных запасов в терригенных коллекторах нефтяных месторождений. Уфа, УГНТУ, 2009, 330 с.
- Габдрахманова К.Ф., Гуторов Ю.А., Ларин П.А. Теория вероятностей и математическая стати-стика в примерах и задачах по разработке нефтяных месторождений (учебное пособие допущено УМО РАЕ по классическому уни-верситетскому и техническому образованию). Уфа:, УГНТУ,2013, 134 с.
- Дипломный проект по теме: “Геофизические методы исследования горизонтальных скважин Федоровского нефтегазового месторождения Западной Сибири”/ Российский государственный геологоразведочный университет, Москва, 2006.
- Мирзаджанзаце А.Х. Математические теории эксперимента в добыче нефти и газа. М. Недра, 1997, 205 с.
References
- Brevdo G.D. Proektirovanie rezhima burenija. M. Nedra, 1988, 200 s.
- Gandzhumjan R.A. Matematicheskaja statistika v razvedochnom burenii: Spravochnoe posobie. M.: Nedra, 1990. 218 s.
- Gutorov Ju.A., Gutorov A.Ju., Voronova E.V. O mehanizme formirovanija ostatochnyh zapasov v terrigennyh kollektorah neftjanyh mestorozhdenij. Ufa, UGNTU, 2009, 330 s.
- Gabdrahmanova K.F., Gutorov Ju.A., Larin P.A. Teorija verojatnostej i matematicheskaja stati-stika v primerah i zadachah po razrabotke neftjanyh mestorozhdenij (uchebnoe posobie dopushheno UMO RAE po klassicheskomu uni-versitetskomu i tehnicheskomu obrazovaniju). Ufa:, UGNTU,2013, 134 s.
- Diplomnyj proekt po teme: “Geofizicheskie metody issledovanija gorizontal'nyh skvazhin Fedorovskogo neftegazovogo mestorozhdenija Zapadnoj Sibiri”/ Rossijskij gosudarstvennyj geologorazvedochnyj universitet, Moskva, 2006.
- Mirzadzhanzace A.H. Matematicheskie teorii jeksperimenta v dobyche nefti i gaza. M. Nedra, 1997, 205 s.