КЛАССИФИКАЦИЯ ЛИНИЙ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
Ушаков А.В.
ORCID: 0000-0002-7665-2086, Кандидат физико-математических наук, Доцент, Московский Городской Педагогический Университет
КЛАССИФИКАЦИЯ ЛИНИЙ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
Аннотация
Статья предназначена студентам и преподавателям педагогических ВУЗов. Она посвящена проблеме классификации линий и поверхностей второго порядка. Это одна из наиболее сложных задач в курсе аналитической геометрии. Очень важно, чтобы студенты осознанно применяли алгоритм ее решения. Поэтому все алгебраические выкладки должны иметь свои наглядные образы. Создавать их можно при помощи компьютерной программы geogebra. Она позволяет выполнять необходимые построения и вычисления. В статье приведены подробные решения двух задач по заявленной теме. Для каждой из них в geogebra подготовлены динамические электронные иллюстрации.
Ключевые слова: Линия, поверхность, классификация, программа geogebra, обучение студентов.
Ushakov A.V.
ORCID: 00000000-0002-7665-2086, PhD in Physics and Mathematics, Associate Professor, Moscow City Pedagogical University
CLASSIFICATION OF LINES AND SURFACES OF SECOND ORDER
Abstract
This article is intended for students and teachers of the pedagogical universities. It is devoted to the problem of classification of lines and quadrics of second order. This is one of the most difficult tasks in the course of analytical geometry. It is very important that students knowingly applied the algorithm of solving it. Therefore all algebraic calculations must have their visual images. You can create them by using the computer program geogebra. It allows you to perform the necessary calculations and builds. The article contains detailed solutions of two tasks on the announced topic. For each of them in geogebra prepared dynamic electronic illustration.
Keywords: line, surface, classification, program geogebra, learning students.
Компьютерная программа geogebra позволяет выполнять различные геометрические построения на плоскости и в пространстве, а также производить все сопутствующие расчеты. Далее мы рассмотрим примеры приведения к каноническому виду алгебраических уравнений второго порядка, определяющих линию или поверхность. Необходимое для этого преобразование координат можно визуализировать в geogebra как результат движения первого рода. В большинстве случаев оно представляет собой либо поворот (на плоскости), либо винтовое движение (в пространстве). Построенные таким образом интерактивные чертежи помогут студентам выявить геометрическую подоплеку решаемой задачи и послужат средством проверки результатов вычислений.
Пример 1. В прямоугольной системе координат ![]() кривая второго порядка имеет уравнение
кривая второго порядка имеет уравнение ![]() . Приведите данное уравнение к каноническому виду, определите вид кривой и постройте ее.
. Приведите данное уравнение к каноническому виду, определите вид кривой и постройте ее.
Решение. Рассмотрим квадратичную форму ![]() с матрицей
с матрицей ![]() . Собственные значения матрицы A являются корнями характеристического уравнения
. Собственные значения матрицы A являются корнями характеристического уравнения ![]() . Далее, найдем собственные векторы матрицы A из условия
. Далее, найдем собственные векторы матрицы A из условия ![]() .
.
При λ=0 имеем ![]() или
или ![]() откуда x=4/3y. При y= –3, получим частное решение
откуда x=4/3y. При y= –3, получим частное решение ![]() .
.
При λ=25 имеем ![]() или
или ![]() откуда x= –3/4y. При y= –4, получим частное решение
откуда x= –3/4y. При y= –4, получим частное решение ![]() .
.
Векторы ![]() принадлежат различным собственным значениям и согласно общей теории образуют ортогональный базис на плоскости. Тогда ортонормированный базис состоит из векторов
принадлежат различным собственным значениям и согласно общей теории образуют ортогональный базис на плоскости. Тогда ортонормированный базис состоит из векторов ![]() . Матрица
. Матрица ![]() перехода от исходного базиса
перехода от исходного базиса ![]() к новому базису
к новому базису ![]() определяет ортогональную замену переменных по закону
определяет ортогональную замену переменных по закону ![]() или
или ![]() В результате, данное уравнение принимает вид
В результате, данное уравнение принимает вид ![]() или
или ![]() . Полагая
. Полагая ![]() получим каноническое уравнение
получим каноническое уравнение ![]() , которое определяет параболу в прямоугольной системе координат
, которое определяет параболу в прямоугольной системе координат ![]() . Связь между исходными и новыми координатами устанавливают формулы
. Связь между исходными и новыми координатами устанавливают формулы ![]() так что O'=(18/5, 1/5).
так что O'=(18/5, 1/5).
Можно доказать, что такому преобразованию координат соответствует повороту вокруг точки S=(11/6, –1/2) на угол ![]() по часовой стрелке. В программе geogebra мы выполним следующие действия:
по часовой стрелке. В программе geogebra мы выполним следующие действия:
- Построим две параболы γ и Г, напечатав в строке ввода их уравнения γ:y^2=2x и Г:9x^2-24xy+16y^2-20x+110y-50=0. Для ввода греческих букв существует специальная кнопка.
- Создадим ползунок для изменения параметра t от 0 до 1. Щелчок инструментом ползунок на графическом поле вызывает диалоговое окно, в котором надо указать имя ползунка, а также его минимальное и максимальное значения.
- Построим точку S, напечатав S=(11/6, -1/2).
- Вычислим углы φ и ψ, напечатав φ=arccos(-4/5) и ψ=t*φ.
- Повернем параболу γ вокруг точки S на угол ψ по часовой стрелке. Инструментом поворот вокруг точки надо щелкнуть последовательно параболу γ и точку S, а в появившемся диалоговом окне указать угол поворота ψ и выбрать направление вращения по часовой стрелке.
- Построим дополнительно базисные векторы и оси координат, после чего скроем все ненужные элементы чертежа, щелкнув значок их видимости на панели объектов.
Если теперь двигать ползунок инструментом перемещение, то можно проследить как парабола γ преобразуется в параболу Г, совершая поворот вокруг точки (рис.1):
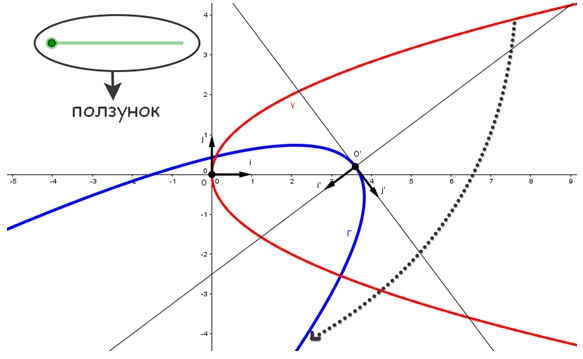
Рис. 1 – Парабола
Пример 2. В прямоугольной системе координат ![]() поверхность второго порядка имеет уравнение
поверхность второго порядка имеет уравнение ![]() . Приведите данное уравнение к каноническому виду, определите вид поверхности и постройте ее.
. Приведите данное уравнение к каноническому виду, определите вид поверхности и постройте ее.
Решение. Рассмотрим квадратичную форму ![]() с матрицей
с матрицей 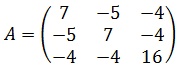 . Собственные значения матрицы A являются корнями характеристического уравнения
. Собственные значения матрицы A являются корнями характеристического уравнения 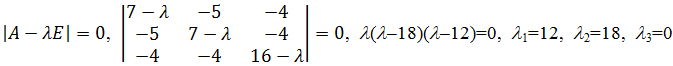 . Далее, найдем собственные векторы матрицы A из условия
. Далее, найдем собственные векторы матрицы A из условия ![]() .
.
При λ=12 имеем 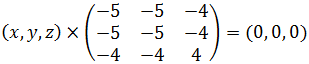 или
или 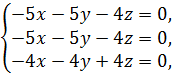 откуда
откуда ![]() При y= –1, получим частное решение
При y= –1, получим частное решение ![]() .
.
При λ=18 имеем 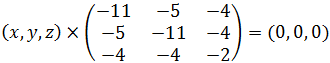 или
или 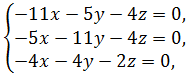 откуда
откуда ![]() При z= –4, получим частное решение
При z= –4, получим частное решение ![]() .
.
При λ=0 имеем 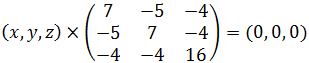 или
или 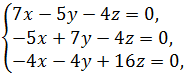 откуда
откуда ![]() При z=1, получим частное решение
При z=1, получим частное решение ![]() .
.
Векторы ![]() принадлежат различным собственным значениям и согласно общей теории образуют ортогональный базис. Тогда ортонормированный базис состоит из векторов
принадлежат различным собственным значениям и согласно общей теории образуют ортогональный базис. Тогда ортонормированный базис состоит из векторов ![]() Матрица
Матрица 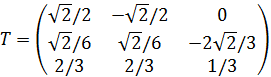 перехода от исходного базиса
перехода от исходного базиса ![]() к новому базису
к новому базису ![]() определяет ортогональную замену переменных по закону
определяет ортогональную замену переменных по закону ![]() или
или 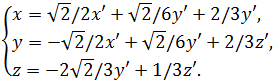 В результате, данное уравнение принимает вид
В результате, данное уравнение принимает вид ![]() или
или ![]() . Полагая
. Полагая 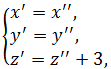 получим каноническое уравнение
получим каноническое уравнение ![]() , которое определяет эллиптический параболоид в прямоугольной декартовой системе координат
, которое определяет эллиптический параболоид в прямоугольной декартовой системе координат ![]() . Связь между исходными и новыми координатами устанавливают формулы
. Связь между исходными и новыми координатами устанавливают формулы 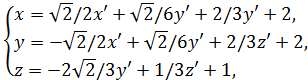 так что O'=(2, 2, 1).
так что O'=(2, 2, 1).
Можно доказать, что такому преобразованию координат соответствует винтовое движение, которое является произведением параллельного переноса на вектор ![]() и поворота на угол
и поворота на угол ![]() по часовой стрелки вокруг прямой l, проходящей через точку
по часовой стрелки вокруг прямой l, проходящей через точку ![]() параллельно вектору
параллельно вектору ![]() . В программе geogebra мы выполним следующие действия:
. В программе geogebra мы выполним следующие действия:
- На полотне 3D объектов построим два параболоида Ф и F, напечатав в строке ввода их уравнения Ф:2x^2+2y^2=4z и F:7x^2+7y^2+16z^2-10xy-8xz-8yz-16x-16y-8z+72=0.
- Построим точки O, O', L, напечатав O=(0, 0, 0), O’=(2, 2, 1), L=((15+9sqrt(2))/7, 0, (-6+9sqrt(2))/14).
- Построим отрезок OO', щелкнув инструментом отрезок его концы. Из контекстного меню переименуем этот отрезок как n.
- Выберем точку А на отрезке OO', щелкнув по нему точка.
- Построим отрезок OA и переименуем его как m.
- Найдем значение параметра t=|OA|/|O'O|, напечатав t=m/n.
- Построим векторы
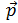 и
и 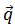 , напечатав p=вектор[((12+3sqrt(2))/14, (6-9sqrt(2))/14, (18-6sqrt(2))/14)] и q=t*p.
, напечатав p=вектор[((12+3sqrt(2))/14, (6-9sqrt(2))/14, (18-6sqrt(2))/14)] и q=t*p. - Построим прямую l, напечатав l=прямая[L, p].
- Вычислим углы φ и ψ, напечатав φ=arccos((sqrt(2)-1)/3) и ψ=t*φ.
- Перенесем параболоид Ф на вектор
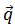 , щелкнув инструментом параллельный перенос по вектору сначала параболоид Ф, а затем вектор q. В результате получим новый параболоид Ф'.
, щелкнув инструментом параллельный перенос по вектору сначала параболоид Ф, а затем вектор q. В результате получим новый параболоид Ф'. - Повернем параболоид Ф' вокруг прямой l на угол ψ по часовой стрелке. Инструментом вращать объект вокруг прямой надо щелкнуть последовательно параболоид F' и прямую l, а в появившемся диалоговом окне указать угол поворота ψ и выбрать направление вращения по часовой стрелке.
- Построим дополнительно базисные векторы и оси координат, после чего скроем все ненужные элементы чертежа, щелкнув значок их видимости на панели объектов.
Если теперь двигать точку А инструментом перемещение от точки О до точки O', то можно проследить как параболоид Ф преобразуется в параболоид F, совершая винтовое движение (рис.2):
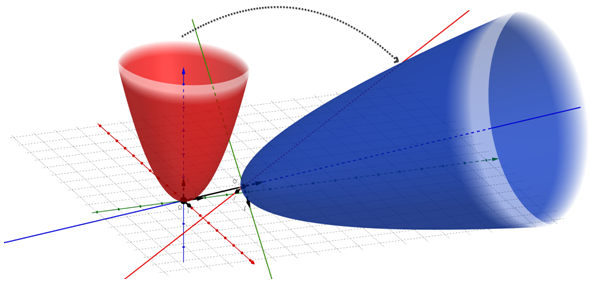
Рис. 2 – Эллиптический параболоид.
Список литературы / References
- Ушаков А.В. О роли примеров на лекциях по топологии в педагогическом ВУЗе / А.В. Ушаков // Педагогические науки. – 2012. – № 3 (54). – С. 74-84.
- Ушаков А.В. О роли примеров на лекциях по дифференциальной геометрии в педагогическом ВУЗе / А.В. Ушаков // Педагогические науки. – 2014. – № 3 (66). – С. 31-34.
- Ушаков А.В. Использование информационных технологий при изучении геометрии в педагогическом ВУЗе / А.В. Ушаков // Педагогические науки. – 2015. – № 2 (71). – С. 55-57.
- Педагогическая направленность математических дисциплин в подготовке будущих учителей математики: Монография / А.В. Ушаков, Ю.А. Семеняченко, В.Г. Покровский и др. – М.: Издательство «Спутник+», 2016. – 144 с.
- Шуркова М.В. Особенности работы над содержанием теорем курса математического анализа на практических занятиях в педагогическом вузе / М.В. Шуркова // Актуальные проблемы гуманитарных и естественных наук. – 2016. – № 2-4. – С. 105-107.
Список литературы на английском языке / References in English
- Ushakov A.V. O roli primerov na lekcijah po topologii v pedagogicheskom VUZe [On the role of examples in lectures on topology in Pedagogical University] / A.V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences] – 2012. – № 3 (54). – P. 74-84. [in Russian]
- Ushakov A.V. O roli primerov na lekcijah po differencial'noj geometrii v pedagogicheskom VUZe [On the role of examples in lectures on differential geometry in the Pedagogical University] / A.V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences] – 2014. – № 3 (66). – P. 31-34. [in Russian]
- Ushakov A.V. Ispol'zovanie informacionnyh tehnologij pri izuchenii geometrii v pedagogicheskom VUZe [The use of information technology in studying geometry at the Pedagogical University] / A.V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences] – 2015. – № 2 (71). – P. 55-57. [in Russian]
- Pedagogicheskaja napravlennost' matematicheskih disciplin v podgotovke budushhih uchitelej matematiki: Monografija [Pedagogical orientation of the mathematical sciences in preparation of future teachers of mathematics: Monograph] / A.V. Ushakov, Ju.A. Semenjachenko, V.G. Pokrovskij and others – M.: Izdatel'stvo «Sputnik+», 2016. – 144 p. [in Russian]
- Shurkova M.V. Osobennosti raboty nad soderzhaniem teorem kursa matematicheskogo analiza na prakticheskih zanjatijah v pedagogicheskom vuze [Features the work of over the content of the course of mathematical analysis on theorems of practical training in the Pedagogical University] / M.V. Shurkova // Aktual'nye problemy gumanitarnyh i estestvennyh nauk [Actual problems of Arts and Sciences] – 2016. – № 2-4. P. – 105-107. [in Russian]
