УНИВЕРСАЛЬНОСТЬ СКЕЙЛИНГА РАЗНООБРАЗИЯ В НЕЙТРАЛЬНЫХ И НИШЕВЫХ МОДЕЛЯХ ЭКОЛОГИЧЕСКИХ СООБЩЕСТВ
Якимов В.Н.1, Гелашвили Д.Б.2, Иудин Д.И.3, Розенберг Г.С.4, Маркелов И.Н.5
1ORCID: 0000-0001-7150-7851, доктор биологических наук, 2Профессор, доктор биологических наук, Нижегородский государственный университет им. Н.И. Лобачевского, 3Доктор биологических наук, доктор физико-математических наук, Институт прикладной физики Российской академии наук, 4Профессор, доктор биологических наук, Институт экологии Волжского бассейна Российской академии наук, 5ORCID: 0000-0002-6974-6033, кандидат биологических наук, Нижегородский государственный университет им. Н.И. Лобачевского
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта №14-04-01548-А
УНИВЕРСАЛЬНОСТЬ СКЕЙЛИНГА РАЗНООБРАЗИЯ В НЕЙТРАЛЬНЫХ И НИШЕВЫХ МОДЕЛЯХ ЭКОЛОГИЧЕСКИХ СООБЩЕСТВ
Аннотация
Проведен анализ зависимости разнообразия от масштаба (скейлинга) в динамических моделях экологических сообществ в ненасыщенном дискретном пространстве с нейтральным и нишевыми механизмами взаимодействия особей. Показано, что ни характер заполнения пространства, ни особенности механизма динамики не влияют на скейлинг разнообразия на качественном уровне. Во всех случаях кривые скейлинга разнообразия имеют аналогичную трехфазную структуру: на малых и больших масштабах наблюдается тривиальный скейлинг (в случае видового богатства – прямая пропорциональность площади), на средних масштабах имеется переходный участок, когда скорость изменения разнообразия уменьшается. Полученные результаты позволили сформулировать гипотезу об универсальности трехфазного характера скейлинга разнообразия, для формирования которого достаточно двух базовых механизмов: поддержания разнообразия за счет баланса между стохастическим вымиранием и видообразованием, а также ограничения распространением, играющего ключевую роль в формировании пространственной структуры.
Ключевые слова: экологическое сообщество, пространственная структура, моделирование, разнообразие, масштаб.
Yakimov B.N.1, Gelashvili D.B.2, Iudin D.I.3, Rozenberg G.S.4, Markelov I.N.5
1ORCID: 0000-0001-7150-7851, PhD in Biology, 2Professor, PhD in Biology, Lobachevsky State University of Nizhni Novgorod, 3PhD in Biology, PhD in Physics and Mathematics, Institute of Applied Physics of the Russian Academy of Sciences, 4Professor, PhD in Biology, Institute of Volga Basin Ecology of the Russian Academy of Sciences, 5 ORCID: 0000-0002-6974-6033, PhD in Biology, Lobachevsky State University of Nizhni Novgorod
UNIVERSALITY OF DIVERSITY SCALING IN NICHE AND NEUTRAL MODELS OF ECOLOGICAL COMMUNITIES
Abstract
We have carried out the analysis of the relation of diversity to the scale in dynamic models of ecological communities in unsaturated discrete space with niche and neutral mechanism of individuals interaction. It was shown that neither space saturation nor details of dynamics mechanism does not influence the diversity scaling qualitatively. Diversity scaling curves in all cases have the same triphasic shape: on small and large scales there is a trivial scaling (the direct proportionality in the case of species richness) and on the middle scales there is a transitional phase with the decrease in the rate of diversity change. On the basis of our results we formulate a hypothesis on the universality of triphasic diversity scaling which is formed by two basic mechanisms: maintaining of diversity by the balance between stochastic extinction and speciation, and dispersal limitation which play a key role in shaping community spatial structure.
Keywords: ecological community, spatial structure, modelling, diversity, scale.
Введение
Зависимость разнообразия от масштаба в экологических сообществах является одной из фундаментальных характеристик структуры биоценозов. В физических науках зависимость некоторого показателя от масштаба, которая описывается степенной функцией, называют скейлингом. В экологии сложилось расширительное толкование этого термина, под которым понимается любая зависимость какого-то показателя от масштаба.
Традиционно скейлинг разнообразия в сообществах изучается в виде зависимости видового богатства от площади, при этом наиболее распространенной функциональной формой является степенная, что соответствует представлениям о фрактальной структуре сообществ [1, 2]. Исследование этой зависимости ведется по двум крупным направлениям: изучение эмпирических зависимостей в натуральных сообществах и их сопоставление с факторами среды и особенностями сообществ, а также теоретическое изучение структуры искусственных сообществ, которое позволяет связать особенности скейлинга с наличием или отсутствием различных механизмов.
Наиболее изученным классом моделей пространственной структуры сообществ являются так называемые нейтральные модели, в основе которых лежит предположение о функциональной эквивалентности особей разных видов с точки зрения их демографических характеристик [3, 4]. Пространственная структура нейтральных моделей характеризуется трехфазным скейлингом видового богатства, когда на малых и больших масштабах имеет место прямая пропорциональность видового богатства площади, а для средних масштабов характерно промежуточное поведение, аппроксимируемое степенным законом. Такой характер скейлинга был продемонстрирован автором нейтральной теории С. Хаббеллом для сообществ с локальным размножением, моделируемых в дискретном пространстве и времени [3]. Позднее это было показано для нейтральных сообществ в дискретном пространстве с реалистичными функциями распространения [5, 6], для сообществ в ненасыщенном дискретном пространстве [7], а также для сообществ в непрерывном пространстве [8].
Нейтральные модели являются упрощением биологической реальности и должны быть использованы в качестве основы для более реалистичных моделей. В контексте изучения скейлинга разнообразия следующим шагом является выяснение влияния нейтральности особей на пространственную структуру модельных сообществ. В настоящей работе мы исследовали скейлинг разнообразия в нейтральных и нишевых моделях в дискретном ненасыщенном пространстве.
Модель и ее параметры
В основе модельного пространства лежит решетка местообитаний, в ячейках которой могут располагаться особи, не перемещающиеся в течение жизни (таким образом, моделируется сообщество прикрепленных организмов). Динамика модели определяется процессами гибели особей, размножения (сопряженного с расселением) и видообразования. Каждый вид обладает параметрами рождаемости b, смертности d и конкурентоспособности. В каждый момент времени каждая особь с определенной вероятностью может погибнуть (в этом случае занимаемая данной особью ячейка становится пустой) и размножиться. При размножении дочерняя особь пытается вселиться в другую ячейку и занимает ее, если эта ячейка вакантна, либо если конкурентоспособность данной особи выше по сравнению с резидентом ячейки (в противном случае имеет место провал размножения). Выбор ячейки для вселения осуществляется в соответствии с функцией плотности нормального распределения со стандартным отклонением L, которое определяет среднюю дистанцию распространения. При размножении с вероятностью ν может произойти мутация и тогда новая особь дает начало новому виду (видообразование путем точеных мутаций).
В нейтральной версии модели все видовые параметры полагаются одинаковыми, при этом рождаемость в два раза превышает смертность (b = 0.5, d = 0.25). Такое соотношение обеспечивает общую заселенность модельного пространства на уровне 50 %. Одинаковая конкурентоспособность означает, что вселение новой особи возможно только в вакантную ячейку.
В нишевой модели на основе компромисса между конкурентоспособностью и смертностью всех видов зафиксирована рождаемость на уровне b = 0.5, а смертность может варьировать от 0 до 0.5. При попытке вселения в занятую ячейку исход конкуренции определяется смертностью: побеждает особь с более высокой смертностью. При реализации компромисса между конкурентоспособностью и рождаемостью смертность зафиксирована на уровне d = 0.25, а рождаемость может варьировать от 0 до 0.5. При попытке вселения в занятую ячейку исход конкуренции определяется рождаемостью: побеждает особь с более низкой рождаемостью. Таким образом, в компромиссных моделях сильные конкуренты обладают негативными демографическими характеристиками: либо они быстрее гибнут, либо медленнее размножаются по сравнению со слабыми конкурентами. За счет этого баланса не происходит конкурентного исключения. При видообразовании ключевой демографический параметр нового вида выбирается случайным образом из указанного диапазона.
Моделирование проводилось на решетках размером 4096 × 4096 ячеек с периодическими граничными условиями, то есть левый ряд ячеек решетки соседствует с правым рядом, а верхний ряд соседствует с нижним. Динамика сообщества моделируется вперед во времени: выбирается начальное состояние и затем итерируется следующая последовательность событий: (1) случайным образом выбирается ячейка на решетке; (2) если эта ячейка занята, моделируется смертность (выбирается случайное число от нуля до единицы и сравнивается с параметром смертности данной особи); (3) если особь не погибла, моделируется рождаемость, сопряженная с расселением и конкуренцией. Моделирование проводилось для трех скоростей видообразования: ν = 10-3, 10-4, 10-5. Для высокой скорости видообразования использовались 8 дистанций распространения L = 5, 7, 9, 11, 13, 16, 23, 32. Для малых скоростей видообразования использовалась дистанция распространения L = 5.
Начальными условиями всегда служила наполовину заселенная решетка. В ходе динамики устанавливается стационарное состояние с относительно постоянным числом особей и видов. Расчет показателей структуры сообщества производился после выхода на стационарный режим.
Для характеристики скейлинга разнообразия мы использовали подход на основе моментов распределения особей по видам [1, 9], которые представляют собой суммы относительных представленностей видов в некоторой степени q, которая называется порядком момента и определяет вклад видов с высокой либо низкой представленностью: ![]() . Многие моменты являются эквивалентами традиционных индексов разнообразия. Так, момент M0 представляет собой видовое богатство S, при M1/2 эквивалентен квадратному корню из индекса Животовского, а момент M2 обратно пропорционален индексу разнообразия Симпсона. Совокупность моментов дает полное представление о разнообразии сообщества на том или ином масштабе с учетом представленностей видов.
. Многие моменты являются эквивалентами традиционных индексов разнообразия. Так, момент M0 представляет собой видовое богатство S, при M1/2 эквивалентен квадратному корню из индекса Животовского, а момент M2 обратно пропорционален индексу разнообразия Симпсона. Совокупность моментов дает полное представление о разнообразии сообщества на том или ином масштабе с учетом представленностей видов.
Анализ скейлинга моментов проводился путем покрытия решетки непересекающимися квадратами различного размера от 1 до полной решетки (значения размеров выбирались равномерно на логарифмической шкале). Для каждого квадрата рассчитывался вектор относительных представленностей видов и набор моментов разнообразия для диапазона порядков моментов от -3 до 3 с шагом 0.1. Моменты для квадратов одинаковой площади усреднялись.
Результаты анализа скейлинга разнообразия
Ранее изученная нейтральная модель в насыщенном пространстве [5, 10] характеризуется универсальностью скейлинга разнообразия по отношению к дистанции распространения. Кривые скейлинга для разных L обладают одинаковой формой, но сдвинуты друг относительно друга. Эта особенность позволяет применить специальную процедуру перемасштабирования осей для получения универсальной кривой скейлинга: площадь заменяется на A/L2, а момент заменяется на величину Mq/L2-2q.
В первую очередь выясним наличие этого свойства для нашей модели, в которой пространство не насыщено особями и имеется большая доля незанятых ячеек. На рис. 1а представлено семейство кривых скейлинга видового богатства для нейтральной модели со скоростью видообразования ν = 10-3 и различными дистанциями распространения. Как и ожидалось, кривые обладают характерной трехфазной формой, причем эта форма не зависит от L, за счет чего достигается формирование единой универсальной кривой, которая представлена на рис. 1б.
На рис. 1в и 1г представлены аналогичные графики для нейтральной модели со скоростью видообразования ν = 10-5. Здесь наблюдается иная картина. Форма трехфазных кривых несколько отличается, вследствие чего не формируется универсальная кривая скейлинга после перемасштабирования осей. На средних масштабах наибольшим наклоном обладает кривая с минимальной дистанцией распространения L = 5, с ростом L снижается и наклон. Такое поведение кривых скейлинга видового богатства объясняется периодическими граничными условиями, из-за которых на больших масштабах рост видового богатства замедляется вследствие того, что в выборке появляются виды, которые присутствуют с другой стороны решетки и уже были учтены при анализе малых масштабов. Мы называем такое поведение эффектом «просачивания» с другой стороны решетки. Просачивание выражено тем сильнее, чем выше средний размер ареала типичного вида, который в свою очередь определяется дистанцией распространения и скоростью видообразования (при прочих равных, чем меньше скорость видообразования, тем меньше на решетке видов и тем больше средний размер ареала). Именно поэтому эффект просачивания практически не заметен при высокой скорости видообразования (рис. 1аб), а при низкой скорости видообразования слабо выражен для малых L.
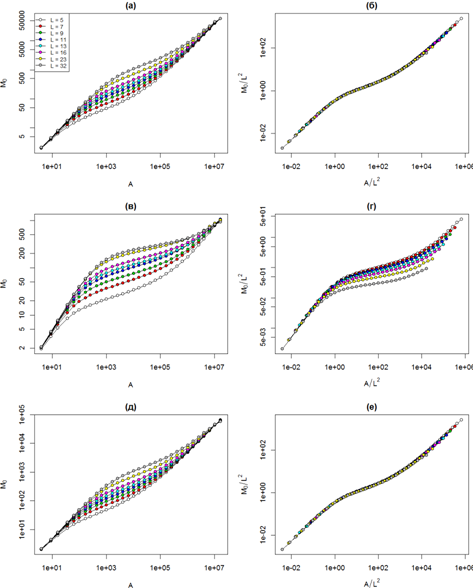
Рис. 1 - Скейлинг видового богатства в нейтральной (а-г) и компромиссной (д-е) модели для скоростей видообразования ν = 10-3 (a, б, д, е) и ν = 10-5 (в, г)
На качественном уровне скейлинг разнообразия в компромиссных моделях не отличается от скейлинга в нейтральной модели. На высоких скоростях видообразования кривые имеют одинаковую трехфазную структуру и формируют единую универсальную кривую после перемасштабирования осей. При снижении скорости видообразования проявляется эффект просачивания, вызывающий снижение скорости изменения моментов разнообразия на больших масштабах. В качестве примера на рис. 1д и 1е представлено семейство кривых скейлинга видового богатства для нишевой модели на основе компромисса между конкурентоспособностью и смертностью со скоростью видообразования ν = 10-3 до и после перемасштабирования осей.
Мы рассматриваем эффект просачивания как артефакт использованных нами граничных условий, искажающий общую картину скейлинга разнообразия. Поэтому при сравнительном анализе моделей с разными механизмами взаимодействия между особями мы рассмотрим кривые для дистанции распространения L = 5, которые подвержены искажению в наименьшей степени. На рис. 2а, 2в и 2д представлены кривые скейлинга видового богатства (момент M0) для трех скоростей видообразования. Во всех случаях на малых масштабах кривые полностью совпадают. При росте масштаба начинают проявляться небольшие отличия, которые выражены тем больше, чем меньше скорость видообразования. На средних и больших масштабах скорость роста разнообразия в нейтральной модели меньше по сравнению с компромиссными.
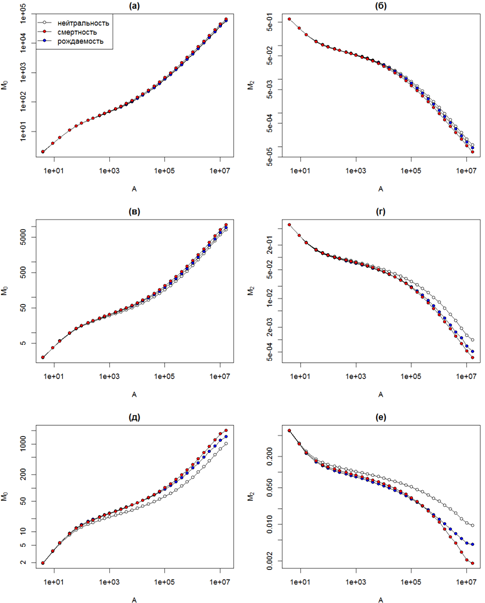
Рис. 2 - Сравнительный анализ скейлинга моментов разнообразия M0 (а, в, д) и M2 (б, г, е) в моделях с разными механизмами взаимодействия между особями для скоростей видообразования ν = 10-3 (a, б), ν = 10-4 (в, г) и ν = 10-5 (д, е)
На рис. 2б, 2г и 2е представлены аналогичные кривые скейлинга момента второго порядка M2. Моменты порядков q > 1 являются обратной мерой разнообразия, поэтому при росте масштаба они не растут, а уменьшаются. Тем не менее, для их скейлинга характерны те же самые тенденции. На малых масштабах кривые для моделей с разными механизмами взаимодействия особей совпадают, на больших масштабах скорость изменения разнообразия в нейтральной модели меньше по сравнению с компромиссными, причем это отличие наиболее выражено для низких скоростей видообразования.
Обсуждение
В настоящей работе рассмотрена пространственная структура экологических сообществ, которые моделируются в ненасыщенном дискретном пространстве на основе разных механизмов взаимодействия особей. В предыдущих исследованиях аналогичного типа рассматривались только нейтральные модели в насыщенном пространстве без незанятых местообитаний [3, 5, 10]. Мы обнаружили, что ненасыщенность пространства не влияет на скейлинг разнообразия на качественном уровне.
Присутствие незанятых ячеек не позволило использовать эффективные генеалогические алгоритмы моделирования назад во времени, которые дают возможность работать с сообществами потенциально неограниченного размера. Мы вынуждены были работать с решетками конечного размера с периодическими границами. В результате при анализе скейлинга разнообразия проявляется эффект просачивания видов с другой стороны решетки, ведущий к снижению скорости роста разнообразия на больших масштабах (рис. 1в, г). Альтернативой периодическим границам являются закрытые границы. Однако в этом случае проявляется другой эффект, связанный со снижением разнообразия вблизи границ, поскольку в приграничных областях приток видов идет только со стороны центра решетки. Этот эффект сильнее искажает кривые скейлинга по сравнению с эффектом просачивания, поскольку он проявляется на всех масштабах.
Помимо нейтральности мы рассмотрели механизм поддержания разнообразия на основе компромисса между конкурентоспособностью и смертностью либо рождаемостью. Скейлинг разнообразия в таких компромиссных моделях качественно соответствует скейлингу в нейтральных моделях (рис. 2): на малых и больших масштабах наблюдается тривиальный скейлинг (в случае видового богатства – прямая пропорциональность площади), на средних масштабах имеется переходный участок, когда скорость изменения разнообразия уменьшается. Для компромиссных моделей характерна независимость формы кривых скейлинга разнообразия от дистанции распространения. Этот результат позволяет поставить вопрос об универсальности трехфазного характера скейлинга разнообразия, который проявляется в моделях с разным типом взаимодействия особей (нейтральные и нишевые), с разным типом реализации пространства (насыщенное и ненасыщенное дискретное, непрерывное), с разными граничными условиями (открытые и периодические границы). Такая универсальность является свидетельством того, что для формирования описанных закономерностей достаточно двух базовых механизмов, присутствующих в моделях всех типов: (1) поддержания разнообразия за счет баланса между стохастическим вымиранием и видообразованием; (2) ограничения распространением, играющего ключевую роль в формировании пространственной структуры. Не вызывает сомнений, что эти механизмы действуют и в природных сообществах, поэтому мы полагаем, что выявленные закономерности скейлинга разнообразия должны быть широко распространены в природе.
При сопоставлении нейтральных и нишевых моделей выявлено, что последние поддерживают большее разнообразие на средних и больших масштабах. Мы полагаем, что дополнительное разнообразие обеспечивается изменчивостью демографических характеристик и локальным сосуществованием видов с разными стратегиями. В модели на основе компромисса со смертностью сильные конкуренты быстро гибнут, но вытесняют в ходе распространения долгоживущих слабых конкурентов. В модели на основе компромисса с рождаемостью сильные конкуренты размножаются существенно медленнее слабых конкурентов, которые быстрее заполняют освобождающееся в результате равномерной смертности пространство.
Скейлинг разнообразия для разных вариантов реализации компромиссного механизма отличается мало, особенно для высоких скоростей видообразования. Некоторые отличия начинают проявляться на малых скоростях видообразования для моментов порядка q > 1. В частности, для момента M2 на средних масштабах скорость изменения выше в модели на основе компромисса с рождаемостью, тогда как на больших масштабах скорость выше уже в модели на основе компромисса со смертностью (рис. 2е). Простой анализ кривых скейлинга разнообразия, проведенный в настоящей работе, не предназначен для выявления тонких деталей пространственной структуры. Такое исследование потребует привлечения более тонких методов анализа, в частности – локального мультифрактального анализа [11].
Список литературы / References
- Гелашвили Д.Б. Фракталы и мультифракталы в биоэкологии / Д.Б. Гелашвили, Г.С. Розенберг, Д.И. Иудин, В.Н. Якимов, Л.А. Солнцев –Н. Новгород: Изд-во ННГУ, 2013. – 370 с.
- Маргалеф Р. Облик биосферы / Р. Маргалеф – М.: Наука, 1992. 254 c.
- Hubbell S.P. The Unified Neutral Theory of Biodiversity and Biogeography / S.P. Hubbell – Princeton University Press, 2011. 375 p.
- Rosindell J. The Unified Neutral Theory of Biodiversity and Biogeography at Age Ten / J. Rosindell, S.P. Hubbell, R.S. Etienne // Trends in Ecology & Evolution. – – Vol. 26. I. 7. – P. 340–348.
- Rosindell J. Species-area relationships from a spatially explicit neutral model in an infinite landscape / J. Rosindell, S.J. Cornell // Ecology Letters. – 2007. – Vol. 10. I. 7. – P. 586–595.
- Rosindell J. Species–area curves, neutral models, and long-distance dispersal / J. Rosindell, S.J. Cornell // Ecology. – 2009. – Vol. 90. I. 7. – P. 1743–1750.
- Cencini M., Pigolotti S., Muñoz M.A. What Ecological Factors Shape Species-Area Curves in Neutral Models? / M. Cencini, S. Pigolotti, M.A. Muñoz // PLoS ONE. – 2012. – Vol. 7. I. 6. – P. e38232.
- Якимов В.Н. Скейлинг разнообразия в нейтральном сообществе, моделируемом в непрерывном пространстве / В.Н. Якимов // Известия Самарского научного центра РАН – 2014. – Т. 16. № – С. 26–35.
- Иудин Д.И. Мультифрактальный анализ структуры биотических сообществ / Д.И. Иудин, Д.Б. Гелашвили, Г.С. Розенберг // Докл. АН. – Т. 389. № 2. – С. 279–282.
- Yakimov B.N. Multifractal analysis of neutral community spatial structure / B.N. Yakimov, D.I. Iudin, L.A. Solntsev, D.B. Gelashvili // Journal of Theoretical Biology. – 2014. – Vol. 343. – P. 44–53.
- Якимов В.Н. Локальный мультифрактальный анализ пространственной структуры луговых сообществ в малых масштабах / В.Н. Якимов, Л.А. Солнцев, Г.С. Розенберг, Д.И. Иудин, А.И. Широков, О.А. Локтева, Д.Б. Гелашвили // Докл. АН. – 2014. – Т. 458. № 5. – С. 613–617.
Список литературы на английском языке / References in English
- Gelashvili D.B. Fraktaly i mul'tifraktaly v biojekologii [Fractals and multifractals in bioecology] / D.B. Gelashvili, G.S. Rozenberg, D.I. Iudin, B.N. Yakimov, L.A. Solntsev – N. Novgorod: Izd-vo NNGU, 2013. – 370 p. [in Russian]
- Margalef R. Oblik biosfery [Our biosphere] / R. Margalef – M.: Nauka, 1992. – 254 [in Russian]
- Hubbell S.P. The Unified Neutral Theory of Biodiversity and Biogeography / S.P. Hubbell – Princeton University Press, 2011. 375 p.
- Rosindell J. The Unified Neutral Theory of Biodiversity and Biogeography at Age Ten / J. Rosindell, S.P. Hubbell, R.S. Etienne // Trends in Ecology & Evolution. – – Vol. 26. I. 7. – P. 340–348.
- Rosindell J. Species-area relationships from a spatially explicit neutral model in an infinite landscape / J. Rosindell, S.J. Cornell // Ecology Letters. – 2007. – Vol. 10. I. 7. – P. 586–595.
- Rosindell J. Species–area curves, neutral models, and long-distance dispersal / J. Rosindell, S.J. Cornell // Ecology. – 2009. – Vol. 90. I. 7. – P. 1743–1750.
- Cencini M., Pigolotti S., Muñoz M.A. What Ecological Factors Shape Species-Area Curves in Neutral Models? / M. Cencini, S. Pigolotti, M.A. Muñoz // PLoS ONE. – 2012. – Vol. 7. I. 6. – P. e38232.
- Yakimov B.N. Skejling raznoobrazija v nejtral'nom soobshhestve, modeliruemom v nepreryvnom prostranstve [Diversity scaling in neutral community modelled in continuous space] / B.N. Yakimov // Izvestija Samarskogo nauchnogo centra RAN [Proceedings of the Samara Scientific Center of the Russian Academy of Sciences] – 2014. – T. 16. № 5. – 26–35. [in Russian]
- Iudin D.I. Mul'tifraktal'nyj analiz struktury bioticheskih soobshhestv [Multifractal analysis of the structure of of biotic communities] / D.I. Iudin, D.B. Gelashvili, G.S. Rozenberg // Dokl. AN. [Reports of the Academy of Sciences] – 2003. T. 389. № 2. – 279–282. [in Russian]
- Yakimov B.N. Multifractal analysis of neutral community spatial structure / B.N. Yakimov, D.I. Iudin, L.A. Solntsev, D.B. Gelashvili // Journal of Theoretical Biology. – 2014. – Vol. 343. – P. 44–53.
- Yakimov B.N. Lokal'nyj mul'tifraktal'nyj analiz prostranstvennoj struktury lugovyh soobshhestv v malyh masshtabah [Local multifractal analysis of meadow communities spatial structure on small scales] / B.N. Yakimov, L.A. Solntsev, G.S. Rozenberg, D.I. Iudin, A.I. Shirokov, O.A. Lokteva, D.B. Gelashvili // Dokl. AN. [Reports of the Academy of Sciences] – 2014. – T. 458. № 5. – 613–617. [in Russian]
