A GAME-THEORETIC MODEL OF DECISION-MAKING IN RISK ENVIRONMENTS (ON THE EXAMPLE OF GAMES IN ECONOMICS)

Принятие управленческих решений в условиях риска – одна из наиболее актуальных задач. Этот процесс основывается на том, что для каждой ситуации развития событий задана вероятность. Появляется возможность проанализировать и выбрать ситуацию с наименьшим уровнем риска, что, в свою очередь, позволяет свести к минимуму возможные негативные последствия.

Комбинирование статических и антагонистических игр совместно с теорией вероятностей, теорией случайных процессов, математической статистикой и другими разделами математики позволяет успешно решать задачи принятия управленческих решений высокой сложности.

Этой теме было посвящено достаточное количество работ как зарубежными, так и отечественными исследователями.

Основополагающим является исследование

В монографии

Рассматривается деятельность производственного предприятия, часть доходов которого идет на покупку активов двух видов, для каждого из них известны ожидаемые прибыли. Необходимо найти план выпуска продукции, прибыль предприятия должна быть максимальной за один период времени, а также найти структуру портфеля, обладающего наименьшим уровнем экономического риска. Реальные данные были получены, согласно отчетам производственного предприятия по деревообработке, осуществляющего деятельность на территории Ленинградской области.

Технологический процесс производства предусматривает производство трех видов продукции (обработка трех видов древесины). Для этого необходимо за один период времени (одна рабочая смена) 30 ед. рабочей силы. Выпуски продукции ограничиваются 10, 12 и 15 условными единицами (тоннами) продукции. Прибыль от выпущенной продукции представляет собой следующие функции: денежных единиц, денежных единиц и денежных единиц соответственно, где – это объем продаж первого вида продукции, – объем продаж второго вида продукции, а – объем продаж третьего вида продукции. Эти данные были получены с помощью аппроксимации результатов реальных доходов фирмы за одну смену в пакете Wolfram Mathematics.

40% от полученной прибыли уходит на покупку активов двух видов, ожидаемые нормы прибыли составляют =20%, =35%, уровень экономических рисков =10%, =13%. Используя теоретико-игровой подход, необходимо определить структуру портфеля, обладающего наименьшим уровнем риска при различных коэффициентах корреляции (=1, =0, =-1).

Для решения поставленной задачи необходимо рассмотреть некоторые базовые теоретические выводы, описанные в работах

Формализация процесса вложения прибыли будет осуществляться с помощью модели Марковица. Ожидаемая норма прибыли и уровень экономического риска определяются выражениями:

(1)

(2)

где – это прибыль, а – это вероятность ее получения.

В модели Марковица структура портфеля задается вектором удельного веса каждого актива: , который удовлетворяет условию неотрицательности долей всех активов:

(3)

Таким образом, в общем виде необходимо решить двухкритериальную задачу, в которой минимизируется риск, и прибыль становится максимальной: ⁡.

Для случая двух активов: , где – доля стоимости первого актива в общей стоимости портфеля, а – доля стоимости второго актива в общей стоимости портфеля. Тогда , как случайные величины, которые характеризуют норму прибыли портфеля и актива i-того вида, соответственно. Их взаимосвязь отражена выражением:

(4)

Двухкритериальная задача поиска оптимального портфеля, состоящего из двух активов, описывается следующим образом:

(5)

(6)

где – это элементы ковариационной матрицы между случайными величинами вкладов , для которой выполняется условие стохастичности, .

Для случая и числовые характеристики составленного портфеля из двух активов рассчитываются в соответствии с выражениями:

(7)

где – коэффициент парной корреляции между и .

(8)

Для портфеля с двумя активами диверсификация оптимизирует уровень экономических рисков только тогда, когда коэффициент парной корреляции норм прибыли активов удовлетворяет условию:

(9)

При выполнении условия , структура портфеля из двух активов, обладающего наименьшим уровнем экономических рисков задается вектором:

(10)

Описанная выше постановка является задачей квадратичного программирования. Перед тем как перейти к решению, необходимо обосновать возможность и корректность решения с помощью антагонистической игры. Данный метод был представлен в работе

- в задаче существует лишь одно линейное ограничение;

- выполняется условие неотрицательности всех коэффициентов.

Рассматривается задача квадратичного программирования следующего вида:

(11)

(12)

где – симметричная матрица квадратичной формы , – заданные действительные числа, ; , , , , -вектор-строка переменных.

Для решения задачи такого вида вводятся вспомогательные переменные и коэффициенты:

(13)

(14)

Для введенных обозначений – симметричная матрица.

(15)

(16)

где – вектор-строка новых переменных.

Решение задачи будет реализовано с помощью функции Лагранжа, в которой – множитель Лагранжа.

Далее будет показана связь задачи квадратичного программирования и классической антагонистической игры.

Матрицы и положительно определенные и симметричные.

Пусть антагонистическая игра задана матрицей С, тогда в данной игре существует вполне смешанная ситуация равновесия . Следовательно, рассматриваемая игра является вполне смешанной игрой, в которой вектор

(17)

где – n-мерный вектор, состоящий из 1 является оптимальным решением задачи (15).

Число , которое определяется выражением , является экстремальным значением функций (11) и (12), где можно найти с помощью .

Поскольку матрица С не содержит седловых точек, а в функции Лагранжа – это стационарная точка и все , то рассматриваемая антагонистическая игра вполне смешанная при этом цена игры удовлетворяет: .

Задача решается в два этапа. Для реализации первой части необходимо составить систему, состоящую из ограничений, соответствующих условиям, и целевой функции на максимум:

(18)

Для решения системы вводятся новые переменные

, , . Далее с учетом замены, система принимает вид:

(19)

(20)

где .

Целевая функция в данном случае имеет квадратичный вид, а также выполняются условия перехода к антагонистической игре. Решение антагонистической игры, заданной симметричной матрицей, в которой нет седловой точки, является стационарной точкой функции Лагранжа для соответствующей задачи квадратичного программирования.

Из системы уравнений определяется оптимальное решение. Вводятся новые переменные: .

Получены результаты .

Система уравнений принимает вид:

(21)

Согласно теоретико-игровым методам определяются смешанные стратегии в игре, заданной симметричной положительно определенной платежной матрицей C квадратичной формы, где коэффициенты матрицы определяются по формуле (17). Полученные коэффициенты: , , , . Матрица имеет вид: .

Собственные значения матрицы , следовательно, – диагональная симметричная положительно определенная матрица, в которой отсутствует седловая точка. Так как матрица квадратная и сумма всех элементов матрицы отлична от нуля, то существует вполне смешанная ситуация равновесия , в которой оптимальны стратегии игроков рассчитываются определены. Полученные значения представлены ниже:

(22)

Цена игры: . Вектор – является оптимальным решением задачи. Следовательно, оптимальным решением исходной задачи являются значения . При этом максимальная прибыль составит денежных единиц.

По условию задачи предприятие вкладывает 40% от прибыли в активы, соответственно примерно 50,7 у.е. идет на формирование инвестиционного портфеля.

Вторая часть задачи будет решаться графически, точки соответствуют однородным портфелям структуры и , при коэффициенте корреляции равном 1. Подставив переменные получим .

Сначала рассчитаем структуру оптимального портфеля при коэффициенте корреляции равном –1. Данное значение коэффициента корреляции является частным и называется абсолютной отрицательной корреляцией, поэтому уровень экономического риска .

Полученное значение ожидаемой нормы прибыли составляет =26,45. Полученные результаты составляют: ≈0,57; ≈0,43.

В результате вычислений получается точка =(0;26,45), соответствующая портфелю , который обладает наименьшим уровнем экономических рисков. При распределении бюджета на актив 1-го вида выделяется 28,9 у.е., а на актив 2 вида выделяется 21,8 у.е.

Также частным является случай, когда коэффициент корреляции принимает нулевое значение. Полученные результаты составляют: = 0,63; =0,37; =25,55; =7,93.

Точка =(7,93;25,55) соответствует портфелю , который обладает наименьшим уровнем экономических рисков, в данном случае. При распределении бюджета на актив 1-го вида выделяется 31.94 у.е., а на актив 2 вида выделяется 18.76 у.е.

На рисунке 1 изображена критериальная плоскость σ0m, где находятся полученные точки. Данные точки имеют следующий смысл:

1. При коэффициенте корреляции , множество всех эффективных портфелей совпадает с множеством всех допустимых портфелей, причем на графике эти множества соответствуют отрезку ;

2. При . Множеству всех эффективных портфелей соответствует отрезок , а множеству всех допустимых портфелей – ломаная линия .

3. При . Множеству всех эффективных портфелей на изображении соответствует отрезок гиперболы, а множеству всех допустимых портфелей ломаная .

Таким образом, положение точки иллюстрирует наиболее «выгодную» позицию с точки зрения вложений и минимизации рисков.

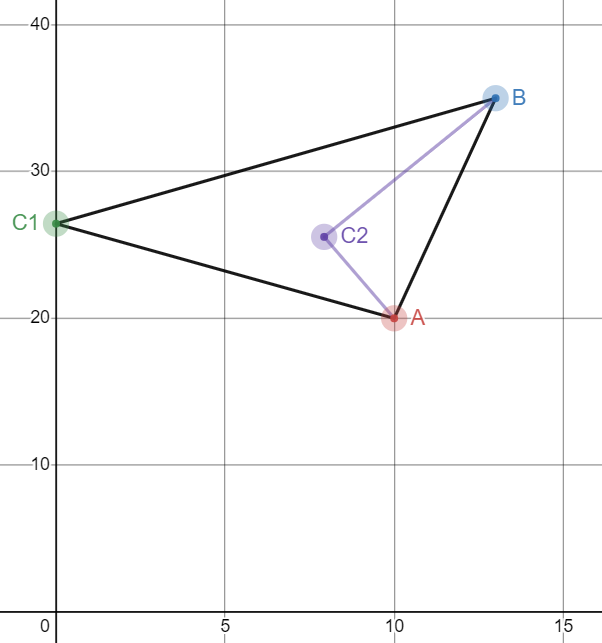
Рисунок 1 - Множество оптимальных и допустимых портфелей

DOI:10.23670/IRJ.2023.133.35.1

6.1. Основные результаты

В работе представлен практический аспект решения задачи квадратичного программирования в формате антагонистической игры. Данные, которые были использованы в моделировании являются реальными, что представляет особый интерес. Результаты численных экспериментов позволяют сделать некоторые выводы о поведении функции прибыли в зависимости от других параметров моделирования. А также определить наименьший уровень риска портфеля при вложении в активы.

6.2. Область применения

Данный подход может быть применен при планировании производства с последующим вложением части прибыли в ценные бумаги. На основании данной модели появляется возможность принимать управленческие решения для максимизации доходов от вложений, а также минимизации рисков.

6.3. Выводы

Результаты моделирования можно сформулировать в виде следующих выводов:

- при увеличении ограничений для каждого вида продукции и коэффициентов функции прибыли для каждого вида продукции достигается максимум прибыли;

- при линейном увеличении коэффициентов функции прибыли максимальная прибыль увеличивается линейно;

- при увеличении ограничений для каждого вида продукции, независимо от коэффициентов функции прибыли значение максимума прибыли увеличивается незначительно;

- чем больше используемые мощности по всем показателям, тем больше прибыль.